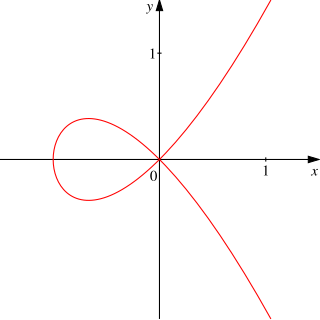In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment . For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.
In commutative algebra, the prime spectrum of a ring R is the set of all prime ideals of R, and is usually denoted by ; in algebraic geometry it is simultaneously a topological space equipped with the sheaf of rings .

In mathematics, topological groups are logically the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures together and consequently they are not independent from each other.
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis. A topological vector space is a vector space that is also a topological space with the property that the vector space operations are also continuous functions. Such a topology is called a vector topology and every topological vector space has a uniform topological structure, allowing a notion of uniform convergence and completeness. Some authors also require that the space is a Hausdorff space. One of the most widely studied categories of TVSs are locally convex topological vector spaces. This article focuses on TVSs that are not necessarily locally convex. Banach spaces, Hilbert spaces and Sobolev spaces are other well-known examples of TVSs.
In mathematics, Hilbert's Nullstellensatz is a theorem that establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields. This relationship was discovered by David Hilbert, who proved the Nullstellensatz in his second major paper on invariant theory in 1893.

In mathematics, complex geometry is the study of geometric structures and constructions arising out of, or described by, the complex numbers. In particular, complex geometry is concerned with the study of spaces such as complex manifolds and complex algebraic varieties, functions of several complex variables, and holomorphic constructions such as holomorphic vector bundles and coherent sheaves. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric aspects of complex analysis.
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments.
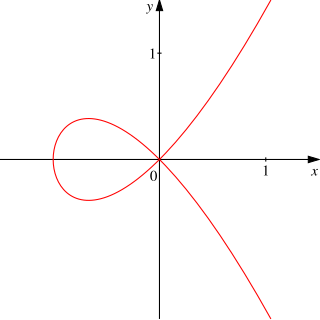
In algebraic geometry, an affine variety, or affine algebraic variety, over an algebraically closed field k is the zero-locus in the affine space kn of some finite family of polynomials of n variables with coefficients in k that generate a prime ideal. If the condition of generating a prime ideal is removed, such a set is called an (affine) algebraic set. A Zariski open subvariety of an affine variety is called a quasi-affine variety.
In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .
In mathematics, a closure operator on a set S is a function :{\mathcal {P}}(S)\rightarrow {\mathcal {P}}(S)} from the power set of S to itself that satisfies the following conditions for all sets
In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. Such involutions sometimes have fixed points, so that the dual of A is A itself. For example, Desargues' theorem is self-dual in this sense under the standard duality in projective geometry.
In the mathematical fields of linear algebra and functional analysis, the orthogonal complement of a subspace W of a vector space V equipped with a bilinear form B is the set W⊥ of all vectors in V that are orthogonal to every vector in W. Informally, it is called the perp, short for perpendicular complement. It is a subspace of V.
In functional and convex analysis, and related disciplines of mathematics, the polar set is a special convex set associated to any subset of a vector space , lying in the dual space The bipolar of a subset is the polar of but lies in .
A Dynkin system, named after Eugene Dynkin is a collection of subsets of another universal set satisfying a set of axioms weaker than those of 𝜎-algebra. Dynkin systems are sometimes referred to as 𝜆-systems or d-system. These set families have applications in measure theory and probability.
Affine geometry, broadly speaking, is the study of the geometrical properties of lines, planes, and their higher dimensional analogs, in which a notion of "parallel" is retained, but no metrical notions of distance or angle are. Affine spaces differ from linear spaces in that they do not have a distinguished choice of origin. So, in the words of Marcel Berger, "An affine space is nothing more than a vector space whose origin we try to forget about, by adding translations to the linear maps." Accordingly, a complex affine space, that is an affine space over the complex numbers, is like a complex vector space, but without a distinguished point to serve as the origin.
In algebraic geometry, a morphism between algebraic varieties is a function between the varieties that is given locally by polynomials. It is also called a regular map. A morphism from an algebraic variety to the affine line is also called a regular function. A regular map whose inverse is also regular is called biregular, and the biregular maps are the isomorphisms of algebraic varieties. Because regular and biregular are very restrictive conditions – there are no non-constant regular functions on projective varieties – the concepts of rational and birational maps are widely used as well; they are partial functions that are defined locally by rational fractions instead of polynomials.
This is a glossary of algebraic geometry.
In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.
In mathematics, a basis of a matroid is a maximal independent set of the matroid—that is, an independent set that is not contained in any other independent set.