
In mathematics and physics, a vector space is a set whose elements, often called vectors, may be added together and multiplied ("scaled") by numbers called scalars. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called vector axioms. Real vector space and complex vector space are kinds of vector spaces based on different kinds of scalars: real coordinate space or complex coordinate space.

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.
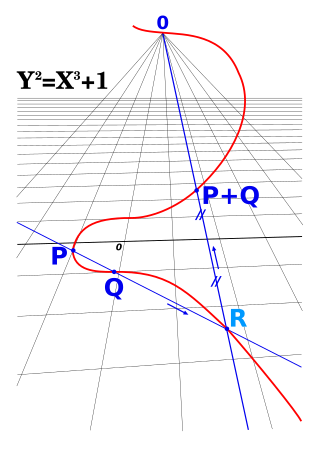
In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .
In linear algebra, a matrix is in row echelon form if it can be obtained as the result of Gaussian elimination. Every matrix can be put in row echelon form by applying a sequence of elementary row operations. The term echelon comes from the French "échelon", and refers to the fact that the nonzero entries of a matrix in row echelon form look like an inverted staircase.
In mathematics, in particular algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects. Such spaces frequently arise as solutions to classification problems: If one can show that a collection of interesting objects can be given the structure of a geometric space, then one can parametrize such objects by introducing coordinates on the resulting space. In this context, the term "modulus" is used synonymously with "parameter"; moduli spaces were first understood as spaces of parameters rather than as spaces of objects. A variant of moduli spaces is formal moduli. Bernhard Riemann first used the term "moduli" in 1857.
In mathematics, the Grassmannian is a differentiable manifold that parameterizes the set of all -dimensional linear subspaces of an -dimensional vector space over a field . For example, the Grassmannian is the space of lines through the origin in , so it is the same as the projective space of one dimension lower than . When is a real or complex vector space, Grassmannians are compact smooth manifolds, of dimension . In general they have the structure of a nonsingular projective algebraic variety.

In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family.
In mathematics, the Plücker map embeds the Grassmannian , whose elements are k-dimensional subspaces of an n-dimensional vector space V, either real or complex, in a projective space, thereby realizing it as a projective algebraic variety. More precisely, the Plücker map embeds into the projectivization of the -th exterior power of . The image is algebraic, consisting of the intersection of a number of quadrics defined by the § Plücker relations.
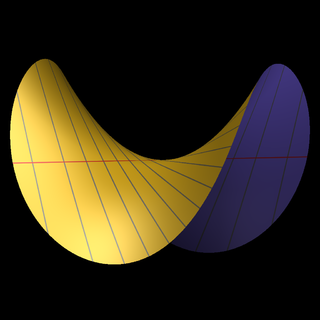
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with the space of all directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point. The metaphor is that of zooming in on a photograph to enlarge part of the picture, rather than referring to an explosion.
In mathematics, particularly in the field of algebraic geometry, a Chow variety is an algebraic variety whose points correspond to effective algebraic cycles of fixed dimension and degree on a given projective space. More precisely, the Chow variety is the fine moduli variety parametrizing all effective algebraic cycles of dimension and degree in .
In mathematics, the tautological bundle is a vector bundle occurring over a Grassmannian in a natural tautological way: for a Grassmannian of -dimensional subspaces of , given a point in the Grassmannian corresponding to a -dimensional vector subspace , the fiber over is the subspace itself. In the case of projective space the tautological bundle is known as the tautological line bundle.
In mathematics, Schubert calculus is a branch of algebraic geometry introduced in the nineteenth century by Hermann Schubert in order to solve various counting problems of projective geometry and, as such, is viewed as part of enumerative geometry. Giving it a more rigorous foundation was the aim of Hilbert's 15th problem. It is related to several more modern concepts, such as characteristic classes, and both its algorithmic aspects and applications remain of current interest. The term Schubert calculus is sometimes used to mean the enumerative geometry of linear subspaces of a vector space, which is roughly equivalent to describing the cohomology ring of Grassmannians. Sometimes it is used to mean the more general enumerative geometry of algebraic varieties that are homogenous spaces of simple Lie groups. Even more generally, Schubert calculus is sometimes understood as encompassing the study of analogous questions in generalized cohomology theories.
In mathematics, intersection theory is one of the main branches of algebraic geometry, where it gives information about the intersection of two subvarieties of a given variety. The theory for varieties is older, with roots in Bézout's theorem on curves and elimination theory. On the other hand, the topological theory more quickly reached a definitive form.
In algebraic geometry, the Chow groups of an algebraic variety over any field are algebro-geometric analogs of the homology of a topological space. The elements of the Chow group are formed out of subvarieties in a similar way to how simplicial or cellular homology groups are formed out of subcomplexes. When the variety is smooth, the Chow groups can be interpreted as cohomology groups and have a multiplication called the intersection product. The Chow groups carry rich information about an algebraic variety, and they are correspondingly hard to compute in general.
In algebraic geometry, a branch of mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space, refining the Chow variety. The Hilbert scheme is a disjoint union of projective subschemes corresponding to Hilbert polynomials. The basic theory of Hilbert schemes was developed by Alexander Grothendieck. Hironaka's example shows that non-projective varieties need not have Hilbert schemes.
In the domain of mathematics known as representation theory, pure spinors are spinors that are annihilated, under the Clifford algebra representation, by a maximal isotropic subspace of a vector space with respect to a scalar product . They were introduced by Élie Cartan in the 1930s and further developed by Claude Chevalley.
In algebraic geometry, determinantal varieties are spaces of matrices with a given upper bound on their ranks. Their significance comes from the fact that many examples in algebraic geometry are of this form, such as the Segre embedding of a product of two projective spaces.
In algebraic geometry, a morphism between algebraic varieties is a function between the varieties that is given locally by polynomials. It is also called a regular map. A morphism from an algebraic variety to the affine line is also called a regular function. A regular map whose inverse is also regular is called biregular, and the biregular maps are the isomorphisms of algebraic varieties. Because regular and biregular are very restrictive conditions – there are no non-constant regular functions on projective varieties – the concepts of rational and birational maps are widely used as well; they are partial functions that are defined locally by rational fractions instead of polynomials.
This is a glossary of algebraic geometry.

In mathematics, a quadric or quadric hypersurface is the subspace of N-dimensional space defined by a polynomial equation of degree 2 over a field. Quadrics are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space. An example is the quadric surface




























