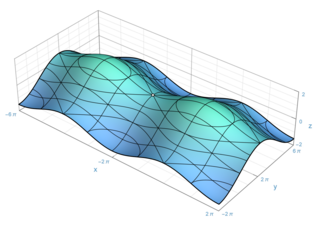
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes. It is a cohomology theory based on the existence of differential forms with prescribed properties.

In mathematics, a foliation is an equivalence relation on an n-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension p, modeled on the decomposition of the real coordinate space Rn into the cosets x + Rp of the standardly embedded subspace Rp. The equivalence classes are called the leaves of the foliation. If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable, or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class Cr it is usually understood that r ≥ 1. The number p is called the dimension of the foliation and q = n − p is called its codimension.

In mathematics, contact geometry is the study of a geometric structure on smooth manifolds given by a hyperplane distribution in the tangent bundle satisfying a condition called 'complete non-integrability'. Equivalently, such a distribution may be given as the kernel of a differential one-form, and the non-integrability condition translates into a maximal non-degeneracy condition on the form. These conditions are opposite to two equivalent conditions for 'complete integrability' of a hyperplane distribution, i.e. that it be tangent to a codimension one foliation on the manifold, whose equivalence is the content of the Frobenius theorem.
This is a glossary of terms specific to differential geometry and differential topology. The following three glossaries are closely related:

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or n-manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space.

In mathematics, systolic geometry is the study of systolic invariants of manifolds and polyhedra, as initially conceived by Charles Loewner and developed by Mikhail Gromov, Michael Freedman, Peter Sarnak, Mikhail Katz, Larry Guth, and others, in its arithmetical, ergodic, and topological manifestations. See also a slower-paced Introduction to systolic geometry.
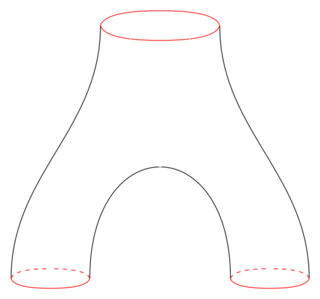
In mathematics, a pair of pants is a surface which is homeomorphic to the three-holed sphere. The name comes from considering one of the removed disks as the waist and the two others as the cuffs of a pair of pants.
In mathematics, a nilmanifold is a differentiable manifold which has a transitive nilpotent group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space and is diffeomorphic to the quotient space , the quotient of a nilpotent Lie group N modulo a closed subgroup H. This notion was introduced by Anatoly Mal'cev in 1951.
In mathematics, a complete manifoldM is a (pseudo-) Riemannian manifold for which, starting at any point p, you can follow a "straight" line indefinitely along any direction. More formally, the exponential map at point p, is defined on TpM, the entire tangent space at p.
In differential geometry, Mikhail Gromov's filling area conjecture asserts that the hemisphere has minimum area among the orientable surfaces that fill a closed curve of given length without introducing shortcuts between its points.
In mathematics, a Riemannian manifold is said to be flat if its Riemann curvature tensor is everywhere zero. Intuitively, a flat manifold is one that "locally looks like" Euclidean space in terms of distances and angles, e.g. the interior angles of a triangle add up to 180°.
In mathematics, specifically geometry and topology, the classification of manifolds is a basic question, about which much is known, and many open questions remain.
In mathematics, Novikov's compact leaf theorem, named after Sergei Novikov, states that
In mathematics, Reeb sphere theorem, named after Georges Reeb, states that
In mathematics, Reeb stability theorem, named after Georges Reeb, asserts that if one leaf of a codimension-one foliation is closed and has finite fundamental group, then all the leaves are closed and have finite fundamental group.
In mathematics the Thurston boundary of Teichmüller space of a surface is obtained as the boundary of its closure in the projective space of functionals on simple closed curves on the surface. It can be interpreted as the space of projective measured foliations on the surface.
In mathematics, a web permits an intrinsic characterization in terms of Riemannian geometry of the additive separation of variables in the Hamilton–Jacobi equation.
In gravitation theory, a world manifold endowed with some Lorentzian pseudo-Riemannian metric and an associated space-time structure is a space-time. Gravitation theory is formulated as classical field theory on natural bundles over a world manifold.










