
In physics, angular momentum is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, frisbees rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it.

In Newtonian mechanics, momentum is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If m is an object's mass and v is its velocity, then the object's momentum p is :

In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example, a particle trapped inside a large box can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow, quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never "sit still". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.

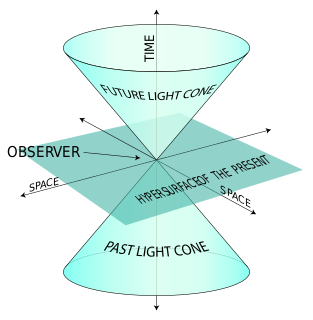
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why different observers perceive differently where and when events occur.

Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
- A body remains at rest, or in motion at a constant speed in a straight line, unless acted upon by a force.
- When a body is acted upon by a force, the time rate of change of its momentum equals the force.
- If two bodies exert forces on each other, these forces have the same magnitude but opposite directions.

The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime. The contravariant four-momentum of a particle with relativistic energy E and three-momentum p = = γmv, where v is the particle's three-velocity and γ the Lorentz factor, is

Time of flight (ToF) is the measurement of the time taken by an object, particle or wave to travel a distance through a medium. This information can then be used to measure velocity or path length, or as a way to learn about the particle or medium's properties. The traveling object may be detected directly or indirectly.
Scintillation is the physical process where a material, called scintillator, emits UV or visible light under excitation from high energy photons or energetic particles,(such as electrons, alpha particles, neutrons or ions). See scintillator and scintillation counter for practical applications.
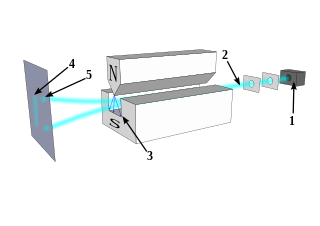
The Stern–Gerlach experiment demonstrated that the spatial orientation of angular momentum is quantized. Thus an atomic-scale system was shown to have intrinsically quantum properties. In the original experiment, silver atoms were sent through a spatially varying magnetic field, which deflected them before they struck a detector screen, such as a glass slide. Particles with non-zero magnetic moment are deflected, due to the magnetic field gradient, from a straight path. The screen reveals discrete points of accumulation, rather than a continuous distribution, owing to their quantized spin. Historically, this experiment was decisive in convincing physicists of the reality of angular-momentum quantization in all atomic-scale systems.
In physics, relativistic mechanics refers to mechanics compatible with special relativity (SR) and general relativity (GR). It provides a non-quantum mechanical description of a system of particles, or of a fluid, in cases where the velocities of moving objects are comparable to the speed of light c. As a result, classical mechanics is extended correctly to particles traveling at high velocities and energies, and provides a consistent inclusion of electromagnetism with the mechanics of particles. This was not possible in Galilean relativity, where it would be permitted for particles and light to travel at any speed, including faster than light. The foundations of relativistic mechanics are the postulates of special relativity and general relativity. The unification of SR with quantum mechanics is relativistic quantum mechanics, while attempts for that of GR is quantum gravity, an unsolved problem in physics.
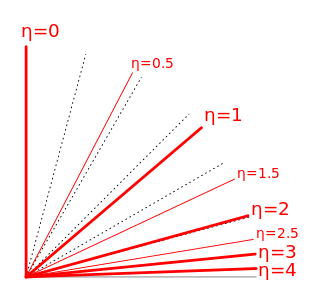
In experimental particle physics, pseudorapidity, , is a commonly used spatial coordinate describing the angle of a particle relative to the beam axis. It is defined as
In quantum mechanics, the probability current is a mathematical quantity describing the flow of probability. Specifically, if one thinks of probability as a heterogeneous fluid, then the probability current is the rate of flow of this fluid. It is a real vector that changes with space and time. Probability currents are analogous to mass currents in hydrodynamics and electric currents in electromagnetism. As in those fields, the probability current is related to the probability density function via a continuity equation. The probability current is invariant under gauge transformation.
The theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles. The motivation uses photons, which are relativistic particles with dynamics described by Maxwell's equations, as an analogue for all types of particles.
Alpha spectrometry is the quantitative study of the energy of alpha particles emitted by a radioactive nuclide that is an alpha emitter.

In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his 1788 work, Mécanique analytique.

Cherenkov radiation is electromagnetic radiation emitted when a charged particle passes through a dielectric medium at a speed greater than the phase velocity of light in that medium. A classic example of Cherenkov radiation is the characteristic blue glow of an underwater nuclear reactor. Its cause is similar to the cause of a sonic boom, the sharp sound heard when faster-than-sound movement occurs. The phenomenon is named after Soviet physicist Pavel Cherenkov.

The NA62 experiment is a fixed-target particle physics experiment in the North Area of the SPS accelerator at CERN. The experiment was approved in February 2007. Data taking began in 2015, and the experiment is expected to become the first in the world to probe the decays of the charged kaon with probabilities down to 10−12. The experiment's spokesperson is Cristina Lazzeroni. The collaboration involves 333 individuals from 30 institutions and 13 countries around the world.
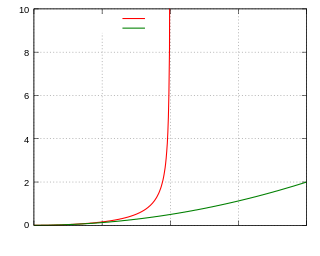
Tests of relativistic energy and momentum are aimed at measuring the relativistic expressions for energy, momentum, and mass. According to special relativity, the properties of particles moving approximately at the speed of light significantly deviate from the predictions of Newtonian mechanics. For instance, the speed of light cannot be reached by massive particles.
Measurements of neutrino speed have been conducted as tests of special relativity and for the determination of the mass of neutrinos. Astronomical searches investigate whether light and neutrinos emitted simultaneously from a distant source are arriving simultaneously on Earth. Terrestrial searches include time of flight measurements using synchronized clocks, and direct comparison of neutrino speed with the speed of other particles.





















