
A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are coprime (that is, they have no common divisor larger than 1). For example, (3, 4, 5) is a primitive Pythagorean triple whereas (6, 8, 10) is not. A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle.
Zeno's paradoxes are a set of philosophical problems devised by the Eleatic Greek philosopher Zeno of Elea.

A right triangle or right-angled triangle (British), or more formally an orthogonal triangle, formerly called a rectangled triangle, is a triangle in which one angle is a right angle, i.e., in which two sides are perpendicular. The relation between the sides and other angles of the right triangle is the basis for trigonometry.

In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance.

In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. For example, if one of the other sides has a length of 3 and the other has a length of 4, then their squares add up to 25. The length of the hypotenuse is the square root of 25, that is, 5.
In mathematics, a proof by infinite descent, also known as Fermat's method of descent, is a particular kind of proof by contradiction used to show that a statement cannot possibly hold for any number, by showing that if the statement were to hold for a number, then the same would be true for a smaller number, leading to an infinite descent and ultimately a contradiction. It is a method which relies on the well-ordering principle, and is often used to show that a given equation, such as a Diophantine equation, has no solutions.
Digital physics is a speculative idea that the universe can be conceived of as a vast, digital computation device, or as the output of a deterministic or probabilistic computer program. The hypothesis that the universe is a digital computer was proposed by Konrad Zuse in his 1969 book Rechnender Raum. The term digital physics was coined by Edward Fredkin in 1978, who later came to prefer the term digital philosophy. Fredkin encouraged the creation of a digital physics group at what was then MIT's Laboratory for Computer Science, with Tommaso Toffoli and Norman Margolus as primary figures.
The Pythagorean trigonometric identity, also called simply the Pythagorean identity, is an identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one of the basic relations between the sine and cosine functions.
The Baudhāyana sūtras are a group of Vedic Sanskrit texts which cover dharma, daily ritual, mathematics and is one of the oldest Dharma-related texts of Hinduism that have survived into the modern age from the 1st-millennium BCE. They belong to the Taittiriya branch of the Krishna Yajurveda school and are among the earliest texts of the genre.
John Earman is an American philosopher of physics. He is an emeritus professor in the History and Philosophy of Science department at the University of Pittsburgh. He has also taught at the University of California, Los Angeles, Rockefeller University, and the University of Minnesota, and was president of the Philosophy of Science Association.
The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold. However, quasicrystals can occur with other diffraction pattern symmetries, such as 5-fold; these were not discovered until 1982 by Dan Shechtman.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.

A Pythagorean prime is a prime number of the form . Pythagorean primes are exactly the odd prime numbers that are the sum of two squares; this characterization is Fermat's theorem on sums of two squares.
In mathematics, Pythagorean addition is a binary operation on the real numbers that computes the length of the hypotenuse of a right triangle, given its two sides. According to the Pythagorean theorem, for a triangle with sides and , this length can be calculated as
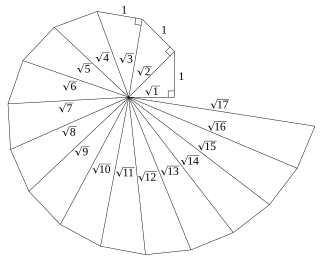
In geometry, the spiral of Theodorus is a spiral composed of right triangles, placed edge-to-edge. It was named after Theodorus of Cyrene.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
In mathematics, statistics and elsewhere, sums of squares occur in a number of contexts:

A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern, but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.
Roman Frigg is a Swiss philosopher, Professor at the London School of Economics and Political Science and director of its Centre for Philosophy of Natural and Social Science. In 2016 he was awarded the Friedrich Wilhelm Bessel Research Award.
David Liggins is a philosopher at the University of Manchester with research interests in metaphysics and philosophy of mathematics.











