In topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

A Möbius strip, Möbius band, or Möbius loop, also spelled Mobius or Moebius, is a surface with only one side and only one boundary. The Möbius strip has the mathematical property of being unorientable. It can be realized as a ruled surface. Its discovery is attributed to the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858, though a structure similar to the Möbius strip can be seen in Roman mosaics dated circa 200–250 AD.

In mathematics, curvature is any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object such as a surface deviates from being a flat plane, or a curve from being straight as in the case of a line, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space – in a way that relates to the radius of curvature of circles that touch the object – and intrinsic curvature, which is defined in terms of the lengths of curves within a Riemannian manifold.

In differential geometry, the Gaussian curvature or Gauss curvatureΚ of a surface at a point is the product of the principal curvatures, κ1 and κ2, at the given point:

In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric.
In mathematics, spaces of non-positive curvature occur in many contexts and form a generalization of hyperbolic geometry. In the category of Riemannian manifolds, one can consider the sectional curvature of the manifold and require that this curvature be everywhere less than or equal to zero. The notion of curvature extends to the category of geodesic metric spaces, where one can use comparison triangles to quantify the curvature of a space; in this context, non-positively curved spaces are known as (locally) CAT(0) spaces.
In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold. Intuitively, a family of surfaces evolves under mean curvature flow if the normal component of the velocity of which a point on the surface moves is given by the mean curvature of the surface. For example, a round sphere evolves under mean curvature flow by shrinking inward uniformly. Except in special cases, the mean curvature flow develops singularities.
In mathematics, specifically differential geometry, a geometric flow is the gradient flow associated to a functional on a manifold which has a geometric interpretation, usually associated with some extrinsic or intrinsic curvature. They can be interpreted as flows on a moduli space or a parameter space.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
In the field of differential geometry in mathematics, inverse mean curvature flow (IMCF) is an example of a geometric flow of hypersurfaces of a Riemannian manifold. Intuitively, a family of surfaces evolves under IMCF if the outward normal speed at which a point on the surface moves is given by the reciprocal of the mean curvature of the surface. For example, a round sphere evolves under IMCF by expanding outward uniformly at an exponentially growing rate. In general, this flow does not exist, and even if it does, it generally develops singularities. Nevertheless, it has recently been an important tool in differential geometry and mathematical problems in general relativity.
The Geometry Festival is an annual mathematics conference held in the United States.
In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form. These concepts were put in their current form with principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.

Simon Brendle is a German mathematician working in differential geometry and nonlinear partial differential equations. He received his Ph.D. from Tübingen University under the supervision of Gerhard Huisken (2001). He was a professor at Stanford University (2005–2016), and is currently a professor at Columbia University. He has held visiting positions at MIT, ETH Zürich, Princeton University, and Cambridge University.
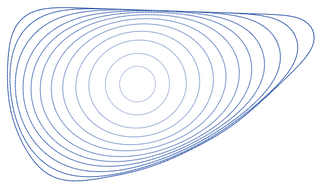
In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.
In mathematics, the stretch factor of an embedding measures the factor by which the embedding distorts distances. Suppose that one metric space S is embedded into another metric space T by a metric map, a continuous one-to-one function f that preserves or reduces the distance between every pair of points. Then the embedding gives rise to two different notions of distance between pairs of points in S. Any pair of points (x,y) in S has both an intrinsic distance, the distance from x to y in S, and a smaller extrinsic distance, the distance from f(x) to f(y) in T. The stretch factor of the pair is the ratio between these two distances, d(x,y)/d(f ,f ). The stretch factor of the whole mapping is the supremum of the stretch factors of all pairs of points. The stretch factor has also been called the distortion or dilation of the mapping.
In differential geometry, Huisken's monotonicity formula states that, if an n-dimensional surface in (n + 1)-dimensional Euclidean space undergoes the mean curvature flow, then its convolution with an appropriately scaled and time-reversed heat kernel is non-increasing. The result is named after Gerhard Huisken, who published it in 1990.