 | This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations .(May 2024) |
In probability theory, Luce's choice axiom, formulated by R. Duncan Luce (1959), [1] states that the probability of selecting one item over another from a pool of many items is not affected by the presence or absence of other items in the pool. Selection of this kind is said to have "independence from irrelevant alternatives" (IIA). [2]
Consider a set of possible outcomes, and consider a selection rule , such that for any with a finite set, the selector selects from with probability .
Luce proposed two choice axioms. The second one is usually meant by "Luce's choice axiom", as the first one is usually called "independence from irrelevant alternatives" (IIA). [3]
Luce's choice axiom 1 (IIA): if , then for any , we still have .
Luce's choice axiom 2 ("path independence"):
for any . [4]
Luce's choice axiom 1 is implied by choice axiom 2.
Define the matching law selection rule , for some "value" function . This is sometimes called the softmax function, or the Boltzmann distribution.
Theorem: Any matching law selection rule satisfies Luce's choice axiom. Conversely, if for all , then Luce's choice axiom implies that it is a matching law selection rule.
In economics, it can be used to model a consumer's tendency to choose one brand of product over another.[ citation needed ]
In behavioral psychology, it is used to model response behavior in the form of matching law.
In cognitive science, it is used to model approximately rational decision processes.
Naive set theory is any of several theories of sets used in the discussion of the foundations of mathematics. Unlike axiomatic set theories, which are defined using formal logic, naive set theory is defined informally, in natural language. It describes the aspects of mathematical sets familiar in discrete mathematics, and suffices for the everyday use of set theory concepts in contemporary mathematics.
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement. Borel sets are named after Émile Borel.
In economics, utility is a measure of the satisfaction that a certain person has from a certain state of the world. Over time, the term has been used in at least two different meanings.
Fuzzy logic is a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false. By contrast, in Boolean logic, the truth values of variables may only be the integer values 0 or 1.
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded.
Independence of irrelevant alternatives (IIA), also known as binary independence, the independence axiom, is an axiom of decision theory and economics describing a necessary condition for rational behavior. The axiom says that a choice between and should not depend on the quality of a third, unrelated outcome .
The expected utility hypothesis is a foundational assumption in mathematical economics concerning decision making under uncertainty. It postulates that rational agents maximize utility, meaning the subjective desirability of their actions. Rational choice theory, a cornerstone of microeconomics, builds this postulate to model aggregate social behaviour.
The Kripke–Platek set theory (KP), pronounced, is an axiomatic set theory developed by Saul Kripke and Richard Platek. The theory can be thought of as roughly the predicative part of ZFC and is considerably weaker than it.
Possibility theory is a mathematical theory for dealing with certain types of uncertainty and is an alternative to probability theory. It uses measures of possibility and necessity between 0 and 1, ranging from impossible to possible and unnecessary to necessary, respectively. Professor Lotfi Zadeh first introduced possibility theory in 1978 as an extension of his theory of fuzzy sets and fuzzy logic. Didier Dubois and Henri Prade further contributed to its development. Earlier, in the 1950s, economist G. L. S. Shackle proposed the min/max algebra to describe degrees of potential surprise.
Robert Duncan Luce was an American mathematician and social scientist, and one of the most preeminent figures in the field of mathematical psychology. At the end of his life, he held the position of Distinguished Research Professor of Cognitive Science at the University of California, Irvine.
Pairwise comparison generally is any process of comparing entities in pairs to judge which of each entity is preferred, or has a greater amount of some quantitative property, or whether or not the two entities are identical. The method of pairwise comparison is used in the scientific study of preferences, attitudes, voting systems, social choice, public choice, requirements engineering and multiagent AI systems. In psychology literature, it is often referred to as paired comparison.
Axiomatic constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language with "" and "" of classical set theory is usually used, so this is not to be confused with a constructive types approach. On the other hand, some constructive theories are indeed motivated by their interpretability in type theories.
Quantal response equilibrium (QRE) is a solution concept in game theory. First introduced by Richard McKelvey and Thomas Palfrey, it provides an equilibrium notion with bounded rationality. QRE is not an equilibrium refinement, and it can give significantly different results from Nash equilibrium. QRE is only defined for games with discrete strategies, although there are continuous-strategy analogues.
The theory of conjoint measurement is a general, formal theory of continuous quantity. It was independently discovered by the French economist Gérard Debreu (1960) and by the American mathematical psychologist R. Duncan Luce and statistician John Tukey.
Polynomial conjoint measurement is an extension of the theory of conjoint measurement to three or more attributes. It was initially developed by the mathematical psychologists David Krantz (1968) and Amos Tversky (1967). The theory was given a comprehensive mathematical exposition in the first volume of Foundations of Measurement, which Krantz and Tversky wrote in collaboration with the mathematical psychologist R. Duncan Luce and philosopher Patrick Suppes. Krantz & Tversky (1971) also published a non-technical paper on polynomial conjoint measurement for behavioural scientists in the journal Psychological Review.
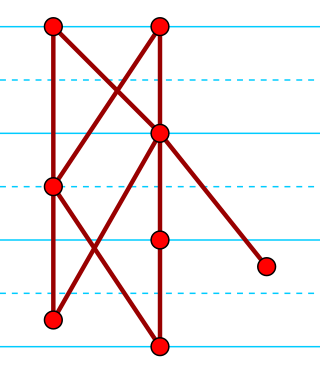
In order theory, a branch of mathematics, a semiorder is a type of ordering for items with numerical scores, where items with widely differing scores are compared by their scores and where scores within a given margin of error are deemed incomparable. Semiorders were introduced and applied in mathematical psychology by Duncan Luce as a model of human preference. They generalize strict weak orderings, in which items with equal scores may be tied but there is no margin of error. They are a special case of partial orders and of interval orders, and can be characterized among the partial orders by additional axioms, or by two forbidden four-item suborders.
Stochastic transitivity models are stochastic versions of the transitivity property of binary relations studied in mathematics. Several models of stochastic transitivity exist and have been used to describe the probabilities involved in experiments of paired comparisons, specifically in scenarios where transitivity is expected, however, empirical observations of the binary relation is probabilistic. For example, players' skills in a sport might be expected to be transitive, i.e. "if player A is better than B and B is better than C, then player A must be better than C"; however, in any given match, a weaker player might still end up winning with a positive probability. Tightly matched players might have a higher chance of observing this inversion while players with large differences in their skills might only see these inversions happen seldom. Stochastic transitivity models formalize such relations between the probabilities and the underlying transitive relation.
In the mathematical discipline of ergodic theory, a Sinai–Ruelle–Bowen (SRB) measure is an invariant measure that behaves similarly to, but is not an ergodic measure. In order to be ergodic, the time average would need to be equal the space average for almost all initial states , with being the phase space. For an SRB measure , it suffices that the ergodicity condition be valid for initial states in a set of positive Lebesgue measure.
In economics and psychology, a random utility model, also called stochastic utility model, is a mathematical description of the preferences of a person, whose choices are not deterministic, but depend on a random state variable.
