
In physics and electrical engineering, a cutoff frequency, corner frequency, or break frequency is a boundary in a system's frequency response at which energy flowing through the system begins to be reduced rather than passing through.

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.

In mathematics, Weierstrass's elliptic functions are elliptic functions that take a particularly simple form; they are named for Karl Weierstrass. This class of functions are also referred to as p-functions and generally written using the symbol ℘. The ℘ functions constitute branched double coverings of the Riemann sphere by the torus, ramified at four points. They can be used to parametrize elliptic curves over the complex numbers, thus establishing an equivalence to complex tori. Genus one solutions of differential equations can be written in terms of Weierstrass elliptic functions. Notably, the simplest periodic solutions of the Korteweg–de Vries equation are often written in terms of Weierstrass p-functions.
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave, and its direction is ordinarily the direction of wave propagation.

In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. These may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called (causal) Green's functions.
In mathematics, the Hamilton–Jacobi equation (HJE) is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations, and is a special case of the Hamilton–Jacobi–Bellman equation. It is named for William Rowan Hamilton and Carl Gustav Jacob Jacobi.
In fluid dynamics, Couette flow is the flow of a viscous fluid in the space between two surfaces, one of which is moving tangentially relative to the other. The configuration often takes the form of two parallel plates or the gap between two concentric cylinders. The flow is driven by virtue of viscous drag force acting on the fluid, but may additionally be motivated by an applied pressure gradient in the flow direction. The Couette configuration models certain practical problems, like flow in lightly loaded journal bearings, and is often employed in viscometry and to demonstrate approximations of reversibility. This type of flow is named in honor of Maurice Couette, a Professor of Physics at the French University of Angers in the late 19th century.
Zero sound is the name given by Lev Landau to the unique quantum vibrations in quantum Fermi liquids.
In functional analysis, compactly supported wavelets derived from Legendre polynomials are termed Legendre wavelets or spherical harmonic wavelets. Legendre functions have widespread applications in which spherical coordinate system is appropriate. As with many wavelets there is no nice analytical formula for describing these harmonic spherical wavelets. The low-pass filter associated to Legendre multiresolution analysis is a finite impulse response (FIR) filter.
In mathematics, a Lamé function, or ellipsoidal harmonic function, is a solution of Lamé's equation, a second-order ordinary differential equation. It was introduced in the paper. Lamé's equation appears in the method of separation of variables applied to the Laplace equation in elliptic coordinates. In some special cases solutions can be expressed in terms of polynomials called Lamé polynomials.

Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load.
In quantum field theory, and especially in quantum electrodynamics, the interacting theory leads to infinite quantities that have to be absorbed in a renormalization procedure, in order to be able to predict measurable quantities. The renormalization scheme can depend on the type of particles that are being considered. For particles that can travel asymptotically large distances, or for low energy processes, the on-shell scheme, also known as the physical scheme, is appropriate. If these conditions are not fulfilled, one can turn to other schemes, like the Minimal subtraction scheme.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.
The solution to the Schrödinger equation, the wavefunction, describes the quantum mechanical properties of a particle on microscopic scales. Measurable quantities such as position, momentum and energy are all derived from the wavefunction.

The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer. As a type of a continuous wavelet, it has been applied in a number of cases, such as in adaptive filters, fractal random fields, and multi-fault classification.
In fluid dynamics, Rayleigh problem also known as Stokes first problem is a problem of determining the flow created by a sudden movement of an infinitely long plate from rest, named after Lord Rayleigh and Sir George Stokes. This is considered as one of the simplest unsteady problem that have exact solution for the Navier-Stokes equations. The impulse movement of semi-infinite plate was studied by Keith Stewartson.
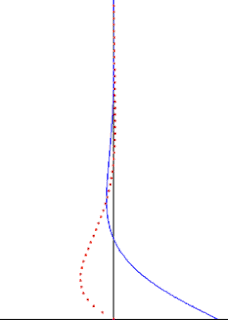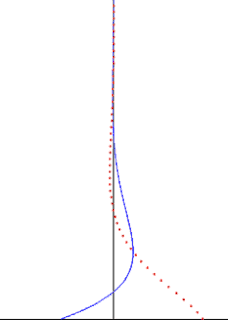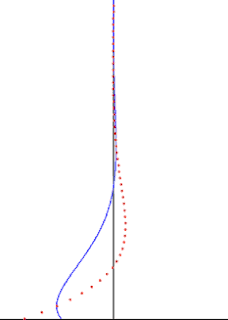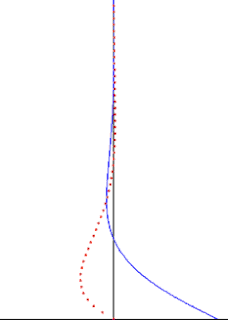
In fluid dynamics, Stokes problem also known as Stokes second problem or sometimes referred to as Stokes boundary layer or Oscillating boundary layer is a problem of determining the flow created by an oscillating solid surface, named after Sir George Stokes. This is considered as one of the simplest unsteady problem that have exact solution for the Navier-Stokes equations. In turbulent flow, this is still named a Stokes boundary layer, but now one has to rely on experiments, numerical simulations or approximate methods in order to obtain useful information on the flow.
In fluid dynamics, Beltrami flows are flows in which the vorticity vector and the velocity vector are parallel to each other. In other words, Beltrami flow is a flow where Lamb vector is zero. It is named after the Italian mathematician Eugenio Beltrami due to his derivation of the Beltrami vector field, while initial developments in fluid dynamics were done by the Russian scientist Ippolit S. Gromeka in 1881.
In representation theory of mathematics, the Waldspurger formula relates the special values of two L-functions of two related admissible irreducible representations. Let k be the base field, f be an automorphic form over k, π be the representation associated via the Jacquet–Langlands correspondence with f. Goro Shimura (1976) proved this formula, when and f is a cusp form; Günter Harder made the same discovery at the same time in an unpublished paper. Marie-France Vignéras (1980) proved this formula, when and f is a newform. Jean-Loup Waldspurger, for whom the formula is named, reproved and generalized the result of Vignéras in 1985 via a totally different method which was widely used thereafter by mathematicians to prove similar formulas.


















































