This article relies largely or entirely on a single source .(November 2010) |
In Euclidean geometry, the AA postulate states that two triangles are similar if they have two corresponding angles congruent.

Euclidean geometry is a mathematical system attributed to Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. The Elements begins with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .
In plane geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in a plane, but this plane does not have to be a Euclidean plane. Angles are also formed by the intersection of two planes in Euclidean and other spaces. These are called dihedral angles. Angles formed by the intersection of two curves in a plane are defined as the angle determined by the tangent rays at the point of intersection. Similar statements hold in space, for example, the spherical angle formed by two great circles on a sphere is the dihedral angle between the planes determined by the great circles.
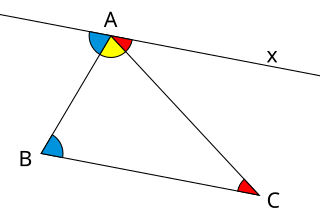
The AA postulate follows from the fact that the sum of the interior angles of a triangle is always equal to 180°. By knowing two angles, such as 32° and 64° degrees, we know that the next angle is 84°, because 180-(32+64)=84. (This is sometimes referred to as the AAA Postulate—which is true in all respects, but two angles are entirely sufficient.)
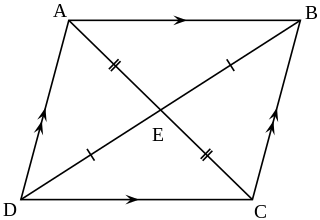
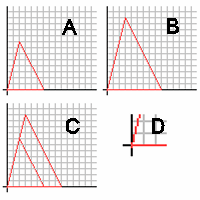
The postulate can be better understood by working in reverse order. The two triangles on grids A and B are similar, by a 1.5 dilation from A to B. If they are aligned, as in grid C, it is apparent that the angle on the origin is congruent with the other (D). We also know that the pair of sides opposite the origin are parallel. We know this because the pairs of sides around them are similar, stem from the same point, and line up with each other. We can then look at the sides around the parallels as transversals, and therefore the corresponding angles are congruent. Using this reasoning we can tell that similar triangles have congruent angles.

Two geometrical objects are called similar if they both have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other. A modern and novel perspective of similarity is to consider geometrical objects similar if one appears congruent to the other when zoomed in or out at some level.
In Euclidean geometry, uniform scaling is a linear transformation that enlarges (increases) or shrinks (diminishes) objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original. A scale factor of 1 is normally allowed, so that congruent shapes are also classed as similar. Uniform scaling happens, for example, when enlarging or reducing a photograph, or when creating a scale model of a building, car, airplane, etc.

In geometry, a transversal is a line that passes through two lines in the same plane at two distinct points. Transversals play a role in establishing whether two other lines in the Euclidean plane are parallel. The intersections of a transversal with two lines create various types of pairs of angles: consecutive interior angles, corresponding angles, and alternate angles. By Euclid's parallel postulate, if the two lines are parallel, consecutive interior angles are supplementary, corresponding angles are equal, and alternate angles are equal.