
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written It is the coefficient of the xk term in the polynomial expansion of the binomial power (1 + x)n; this coefficient can be computed by the multiplicative formula
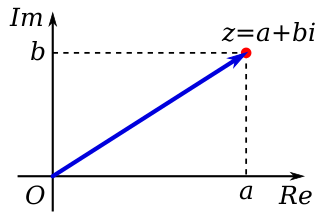
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary unit and satisfying the equation ; every complex number can be expressed in the form , where a and b are real numbers. Because no real number satisfies the above equation, i was called an imaginary number by René Descartes. For the complex number ,a is called the real part, and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols or C. Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world.
In number theory, given a prime number p, the p-adic numbers form an extension of the rational numbers which is distinct from the real numbers, though with some similar properties; p-adic numbers can be written in a form similar to decimals, but with digits based on a prime number p rather than ten, and extending to the left rather than to the right.
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.
In mathematics, Hilbert's Nullstellensatz is a theorem that establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields. This relationship was discovered by David Hilbert, who proved the Nullstellensatz in his second major paper on invariant theory in 1893.

In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials: the Hermite polynomials, Laguerre polynomials, Jacobi polynomials.
In mathematics, and more specifically in computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating set of an ideal in a polynomial ring K[x1, ..., xn] over a field K. A Gröbner basis allows many important properties of the ideal and the associated algebraic variety to be deduced easily, such as the dimension and the number of zeros when it is finite. Gröbner basis computation is one of the main practical tools for solving systems of polynomial equations and computing the images of algebraic varieties under projections or rational maps.
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rational numbers; they may be taken in any field K. In this case, one speaks of a rational function and a rational fraction over K. The values of the variables may be taken in any field L containing K. Then the domain of the function is the set of the values of the variables for which the denominator is not zero, and the codomain is L.
In mathematics, specifically algebraic geometry, a scheme is a structure that enlarges the notion of algebraic variety in several ways, such as taking account of multiplicities and allowing "varieties" defined over any commutative ring.
In mathematics, differential algebra is, broadly speaking, the area of mathematics consisting in the study of differential equations and differential operators as algebraic objects in view of deriving properties of differential equations and operators without computing the solutions, similarly as polynomial algebras are used for the study of algebraic varieties, which are solution sets of systems of polynomial equations. Weyl algebras and Lie algebras may be considered as belonging to differential algebra.
In mathematics, the resultant of two polynomials is a polynomial expression of their coefficients that is equal to zero if and only if the polynomials have a common root, or, equivalently, a common factor. In some older texts, the resultant is also called the eliminant.
In algebra, the greatest common divisor of two polynomials is a polynomial, of the highest possible degree, that is a factor of both the two original polynomials. This concept is analogous to the greatest common divisor of two integers.
A hyperelliptic curve is a particular kind of algebraic curve. There exist hyperelliptic curves of every genus . If the genus of a hyperelliptic curve equals 1, we simply call the curve an elliptic curve. Hence we can see hyperelliptic curves as generalizations of elliptic curves. There is a well-known group structure on the set of points lying on an elliptic curve over some field , which we can describe geometrically with chords and tangents. Generalizing this group structure to the hyperelliptic case is not straightforward. We cannot define the same group law on the set of points lying on a hyperelliptic curve, instead a group structure can be defined on the so-called Jacobian of a hyperelliptic curve. The computations differ depending on the number of points at infinity. Imaginary hyperelliptic curves are hyperelliptic curves with exactly 1 point at infinity: real hyperelliptic curves have two points at infinity.
Petkovšek's algorithm is a computer algebra algorithm that computes a basis of hypergeometric terms solution of its input linear recurrence equation with polynomial coefficients. Equivalently, it computes a first order right factor of linear difference operators with polynomial coefficients. This algorithm was developed by Marko Petkovšek in his PhD-thesis 1992. The algorithm is implemented in all the major computer algebra systems.
In the study of differential equations, the Loewy decomposition breaks every linear ordinary differential equation (ODE) into what are called largest completely reducible components. It was introduced by Alfred Loewy.

In mathematics, an infinite sequence of numbers is called constant-recursive if it satisfies an equation of the form
In mathematics, the Fuchs relation is a relation between the starting exponents of formal series solutions of certain linear differential equations, so called Fuchsian equations. It is named after Lazarus Immanuel Fuchs.
In mathematics a P-recursive equation can be solved for polynomial solutions. Sergei A. Abramov in 1989 and Marko Petkovšek in 1992 described an algorithm which finds all polynomial solutions of those recurrence equations with polynomial coefficients. The algorithm computes a degree bound for the solution in a first step. In a second step an ansatz for a polynomial of this degree is used and the unknown coefficients are computed by a system of linear equations. This article describes this algorithm.
In mathematics a P-recursive equation is a linear equation of sequences where the coefficient sequences can be represented as polynomials. P-recursive equations are linear recurrence equations with polynomial coefficients. These equations play an important role in different areas of mathematics, specifically in combinatorics. The sequences which are solutions of these equations are called holonomic, P-recursive or D-finite.

















































