This article relies largely or entirely on a single source .(March 2024) |
An adaptive k-d tree is a tree for multidimensional points where successive levels may be split along different dimensions.
This article relies largely or entirely on a single source .(March 2024) |
An adaptive k-d tree is a tree for multidimensional points where successive levels may be split along different dimensions.
In computer science, an associative array, map, symbol table, or dictionary is an abstract data type that stores a collection of pairs, such that each possible key appears at most once in the collection. In mathematical terms, an associative array is a function with finite domain. It supports 'lookup', 'remove', and 'insert' operations.

A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information".
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable. Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics.
In computing, a persistent data structure or not ephemeral data structure is a data structure that always preserves the previous version of itself when it is modified. Such data structures are effectively immutable, as their operations do not (visibly) update the structure in-place, but instead always yield a new updated structure. The term was introduced in Driscoll, Sarnak, Sleator, and Tarjan's 1986 article.

In signal processing, a filter bank is an array of bandpass filters that separates the input signal into multiple components, each one carrying a sub-band of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components differently and recombine them into a modified version of the original signal. The process of decomposition performed by the filter bank is called analysis ; the output of analysis is referred to as a subband signal with as many subbands as there are filters in the filter bank. The reconstruction process is called synthesis, meaning reconstitution of a complete signal resulting from the filtering process.

In computer science, a k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. K-dimensional is that which concerns exactly k orthogonal axes or a space of any number of dimensions. k-d trees are a useful data structure for several applications, such as:

In mathematical analysis and computer science, functions which are Z-order, Lebesgue curve, Morton space-filling curve, Morton order or Morton code map multidimensional data to one dimension while preserving locality of the data points. It is named in France after Henri Lebesgue, who studied it in 1904, and named in the United States after Guy Macdonald Morton, who first applied the order to file sequencing in 1966. The z-value of a point in multidimensions is simply calculated by interleaving the binary representations of its coordinate values. Once the data are sorted into this ordering, any one-dimensional data structure can be used, such as simple one dimensional arrays, binary search trees, B-trees, skip lists or hash tables. The resulting ordering can equivalently be described as the order one would get from a depth-first traversal of a quadtree or octree.
A vantage-point tree is a metric tree that segregates data in a metric space by choosing a position in the space and partitioning the data points into two parts: those points that are nearer to the vantage point than a threshold, and those points that are not. By recursively applying this procedure to partition the data into smaller and smaller sets, a tree data structure is created where neighbors in the tree are likely to be neighbors in the space.
A metric tree is any tree data structure specialized to index data in metric spaces. Metric trees exploit properties of metric spaces such as the triangle inequality to make accesses to the data more efficient. Examples include the M-tree, vp-trees, cover trees, MVP trees, and BK-trees.

The UB-tree as proposed by Rudolf Bayer and Volker Markl is a balanced tree for storing and efficiently retrieving multidimensional data. It is basically a B+ tree with records stored according to Z-order, also called Morton order. Z-order is simply calculated by bitwise interlacing the keys.
Nearest neighbor search (NNS), as a form of proximity search, is the optimization problem of finding the point in a given set that is closest to a given point. Closeness is typically expressed in terms of a dissimilarity function: the less similar the objects, the larger the function values.

In computer science, the range searching problem consists of processing a set S of objects, in order to determine which objects from S intersect with a query object, called the range. For example, if S is a set of points corresponding to the coordinates of several cities, find the subset of cities within a given range of latitudes and longitudes.
In computer science, a range tree is an ordered tree data structure to hold a list of points. It allows all points within a given range to be reported efficiently, and is typically used in two or higher dimensions. Range trees were introduced by Jon Louis Bentley in 1979. Similar data structures were discovered independently by Lueker, Lee and Wong, and Willard. The range tree is an alternative to the k-d tree. Compared to k-d trees, range trees offer faster query times of but worse storage of , where n is the number of points stored in the tree, d is the dimension of each point and k is the number of points reported by a given query.
In applied mathematics, topological data analysis (TDA) is an approach to the analysis of datasets using techniques from topology. Extraction of information from datasets that are high-dimensional, incomplete and noisy is generally challenging. TDA provides a general framework to analyze such data in a manner that is insensitive to the particular metric chosen and provides dimensionality reduction and robustness to noise. Beyond this, it inherits functoriality, a fundamental concept of modern mathematics, from its topological nature, which allows it to adapt to new mathematical tools.

In network theory, multidimensional networks, a special type of multilayer network, are networks with multiple kinds of relations. Increasingly sophisticated attempts to model real-world systems as multidimensional networks have yielded valuable insight in the fields of social network analysis, economics, urban and international transport, ecology, psychology, medicine, biology, commerce, climatology, physics, computational neuroscience, operations management, and finance.
This article provides a short survey of the concepts, principles and applications of Multirate Filter Banks and Multidimensional Directional Filter Banks.

Vijay Kumar Vaishnavi is a noted researcher and scholar in the computer information systems field with contributions mainly in the areas of design science, software engineering, and data structures & algorithms, authoring over 150 publications including seven books in these and related areas, and co-owning a patent. He is currently Professor Emeritus at the Department of Computer Information Systems, Georgia State University. He is Senior Editor Emeritus of MIS Quarterly and is on the editorial boards of a number of other major journals. His research has been funded by the National Science Foundation (NSF) as well as by the industry.
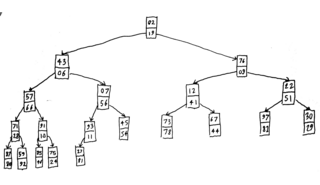
A K-D heap is a data structure in computer science which implements a multidimensional priority queue without requiring additional space. It is a generalization of the Heap. It allows for efficient insertion, query of the minimum element, and deletion of the minimum element in any of the k dimensions, and therefore includes the double-ended heap as a special case.
The PH-tree is a tree data structure used for spatial indexing of multi-dimensional data (keys) such as geographical coordinates, points, feature vectors, rectangles or bounding boxes. The PH-tree is space partitioning index with a structure similar to that of a quadtree or octree. However, unlike quadtrees, it uses a splitting policy based on tries and similar to Crit bit trees that is based on the bit-representation of the keys. The bit-based splitting policy, when combined with the use of different internal representations for nodes, provides scalability with high-dimensional data. The bit-representation splitting policy also imposes a maximum depth, thus avoiding degenerated trees and the need for rebalancing.
![]() This article incorporates public domain material from Paul E. Black. "Adaptive k-d tree". Dictionary of Algorithms and Data Structures . NIST.
This article incorporates public domain material from Paul E. Black. "Adaptive k-d tree". Dictionary of Algorithms and Data Structures . NIST.