Apeirogonal tiling

Last updated March 10, 2019

In geometry, an apeirogonal tiling is a tessellation of the Euclidean plane, hyperbolic plane, or some other two-dimensional space by apeirogons. Tilings of this type include:

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellations can be generalized to higher dimensions and a variety of geometries.

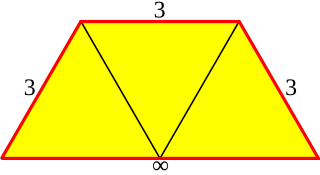
In geometry, an apeirogon is a generalized polygon with a countably infinite number of sides. It can be considered as the limit of an n-sided polygon as n approaches infinity. The interior of a linear apeirogon can be defined by a direction order of vertices, and defining half the plane as the interior.

Order-2 apeirogonal tiling, Euclidean tiling of two half-spaces
Order-3 apeirogonal tiling, hyperbolic tiling with 3 apeirogons around a vertex
Order-4 apeirogonal tiling, hyperbolic tiling with 4 apeirogons around a vertex
Order-5 apeirogonal tiling, hyperbolic tiling with 5 apeirogons around a vertex
Infinite-order apeirogonal tiling, hyperbolic tiling with an infinite number of apeirogons around a vertex

In geometry, an order-2 apeirogonal tiling, apeirogonal dihedron, or infinite dihedron is a tiling of the plane consisting of two apeirogons. It may be considered an improper regular tiling of the Euclidean plane, with Schläfli symbol {∞, 2}. Two apeirogons, joined along all their edges, can completely fill the entire plane as an apeirogon is infinite in size and has an interior angle of 180°, which is half of a full 360°.

In geometry, the order-3 apeirogonal tiling is a regular tiling of the hyperbolic plane. It is represented by the Schläfli symbol {∞,3}, having three regular apeirogons around each vertex. Each apeirogon is inscribed in a horocycle.

In geometry, the order-4 apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,4}.

Related Research Articles

In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.

In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-transitive.

In the field of hyperbolic geometry, the order-4 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is called paracompact because it has infinite cells. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

The order-6 cubic honeycomb is a paracompact regular space-filling tessellations in hyperbolic 3-space. It is called paracompact because it has infinite vertex figures, with all vertices as ideal points at infinity. With Schläfli symbol {4,3,6}, it has six cubes meeting along each edge. Its vertex figure is an infinite triangular tiling. It is dual is the order-4 hexagonal tiling honeycomb.

In the field of hyperbolic geometry, the order-5 hexagonal tiling honeycomb arises one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is called paracompact because it has infinite cells. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

In the field of hyperbolic geometry, the order-6 hexagonal tiling honeycomb arises one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is called paracompact because it has infinite cells. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

In the geometry of hyperbolic 3-space, the order-4 square tiling honeycomb, is one of 11 paracompact regular honeycombs. It is called paracompact because it has infinite cells and vertex figures, with all vertices as ideal points at infinity. Given by Schläfli symbol {4,4,4}, has four square tilings, {4,4} around each edge, and infinite square tilings around each vertex in a square tiling {4,4} vertex arrangement.

In geometry, the order-5 apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,5}.

In the geometry of hyperbolic 3-space, the order-3-7 heptagonal honeycomb a regular space-filling tessellation with Schläfli symbol {7,3,7}.

In geometry, the order-6 apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,6}.

In the geometry of hyperbolic 3-space, the order-7-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,7,3}.

In the geometry of hyperbolic 3-space, the order-6-4 square honeycomb a regular space-filling tessellation with Schläfli symbol {4,6,4}.

In the geometry of hyperbolic 3-space, the order-8-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,8,3}.

In the geometry of hyperbolic 3-space, the order-infinite-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,∞,3}.

Apeirogonal tiling

See also

Related Research Articles