Apeirogonal prism

Apeirogonal prism
Type	Semiregular tiling
Vertex configuration	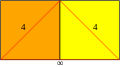4.4.∞
Schläfli symbol	t{2,∞}
Wythoff symbol	2 ∞| 2
Coxeter diagram
Symmetry	[∞,2], (*∞22)
Rotation symmetry	[∞,2]+, (∞22)
Bowers acronym	Azip
Dual	Apeirogonal bipyramid
Properties	Vertex-transitive

In geometry, an apeirogonal prism or infinite prism is the arithmetic limit of the family of prisms; it can be considered an infinite polyhedron or a tiling of the plane. ^[1]

Thorold Gosset called it a 2-dimensional semi-check, like a single row of a checkerboard.^{[ citation needed ]}

If the sides are squares, it is a uniform tiling. If colored with two sets of alternating squares it is still uniform.^{[ citation needed ]}

• 
  Uniform variant with alternate colored square faces.
• 
  Its dual tiling is an apeirogonal bipyramid.

Related tilings and polyhedra

The apeirogonal tiling is the arithmetic limit of the family of prisms t{2, p} or p.4.4, as p tends to infinity, thereby turning the prism into a Euclidean tiling.

An alternation operation can create an apeirogonal antiprism composed of three triangles and one apeirogon at each vertex.

Similarly to the uniform polyhedra and the uniform tilings, eight uniform tilings may be based from the regular apeirogonal tiling. The rectified and cantellated forms are duplicated, and as two times infinity is also infinity, the truncated and omnitruncated forms are also duplicated, therefore reducing the number of unique forms to four: the apeirogonal tiling, the apeirogonal hosohedron, the apeirogonal prism, and the apeirogonal antiprism.

Order-2 regular or uniform apeirogonal tilings

(∞ 2 2)	Wythoff symbol	Schläfli symbol	Coxeter diagram	Vertex config.	Tiling image	Tiling name
Parent	2 | ∞ 2	{∞,2}		∞.∞		Apeirogonal dihedron
Truncated	2 2 | ∞	t{∞,2}		2.∞.∞
Rectified	2 | ∞ 2	r{∞,2}		2.∞.2.∞
Birectified (dual)	∞ | 2 2	{2,∞}		2∞		Apeirogonal hosohedron
Bitruncated	2 ∞ | 2	t{2,∞}		4.4.∞		Apeirogonal prism
Cantellated	∞ 2 | 2	rr{∞,2}
Omnitruncated (Cantitruncated)	∞ 2 2 |	tr{∞,2}		4.4.∞
Snub	| ∞ 2 2	sr{∞,2}		3.3.3.∞		Apeirogonal antiprism

Notes

1. Conway (2008), p.263

References

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns . W. H. Freeman and Company. ISBN   0-7167-1193-1.
• Conway, John H.; Heidi Burgiel; Chaim Goodman-Strauss (2008). The Symmetries of Things. Taylor & Francis. ISBN   978-1-56881-220-5.