List of tessellations

This is a list of tessellations.

Spherical

Regular Spherical (n=1, 2, 3, ...)
Article	Vertex configuration	Schläfli symbol	Image
Dihedron	n2	{n,2}	{6,2}
Hosohedron	2n	{2,n}	{2,6}
Spherical tetrahedron	33	{3,3}
Spherical octahedron	34	{3,4}
Spherical cube	43	{4,3}
Spherical icosahedron	35	{3,5}
Spherical dodecahedron	53	{5,3}

Semi-regular Spherical (n=2, 3, ...)
Article	Vertex configuration	Schläfli symbol	Image
Prism	4.4.n	t{2, n} = { }×{n}	{ }×{6}
Antiprism	33.n	sr{2,n} = { }⊗{n}	{ }⊗{6}

Dual semi-regular Spherical (n=2, 3, ...)
Article	Vertex configuration	Schläfli symbol	Image
Bipyramid	V42.n	dt{2, n} = { }+{n}	{ }+{6}
Trapezohedron	V33.n	dsr{2,n} = { }⨁{n}	{ }⨁{6}

Planar

Regular
Article	Vertex configuration	Schläfli symbol	Image
Apeirogonal hosohedron	2∞	{2,∞}
Order-2 apeirogonal tiling	∞2	{∞,2}
Square tiling	44	{4,4}
Triangular tiling	36	{3,6}
Hexagonal tiling	63	{6,3}

Semi-regular
Article	Vertex configuration	Schläfli symbol	Image
Apeirogonal prism	42.∞	t{2,∞}
Apeirogonal antiprism	33.∞	sr{2,∞}
Snub square tiling	32.4.3.4	s{4,4}
Elongated triangular tiling	33.42	{3,6}:e
Snub trihexagonal tiling	34.6	sr{6,3}
Rhombitrihexagonal tiling	3.4.6.4	rr{6,3}
Trihexagonal tiling	3.6.3.6	r{6,3}
Truncated hexagonal tiling	3.122	t{6,3}
Truncated trihexagonal tiling	4.6.12	tr{6,3}
Truncated square tiling	4.82	tr{4,4}

Dual semi-regular
Article	Face configuration	Schläfli symbol	Image
Apeirogonal deltohedron	V33.∞	dsr{2,∞}
Apeirogonal bipyramid	V42.∞	dt{2,∞}
Cairo pentagonal tiling	V32.4.3.4	ds{4,4}
Prismatic pentagonal tiling	V33.42	d{3,6}:e
Floret pentagonal tiling	V34.6	dsr{6,3}
Deltoidal trihexagonal tiling	V3.4.6.4	drr{6,3}
Rhombille tiling	V3.6.3.6	dr{6,3}
Triakis triangular tiling	V3.122	dt{6,3}
Kisrhombille tiling	V4.6.12	dtr{6,3}
Tetrakis square tiling	4.82	tr{4,4}

Hyperbolic

Hyperbolic
Article	Vertex configuration	Schläfli symbol	Image
Snub tetrapentagonal tiling	32.4.3.5	sr{5,4}
Snub tetrahexagonal tiling	32.4.3.6	sr{6,4}
Snub tetraheptagonal tiling	32.4.3.7	sr{7,4}
Snub tetraoctagonal tiling	32.4.3.8	sr{8,4}
Snub tetraapeirogonal tiling	32.4.3.∞	sr{∞,4}
Snub pentapentagonal tiling	32.5.3.5	s{5,4}
Snub pentahexagonal tiling	32.5.3.6	sr{6,5}
Snub hexahexagonal tiling	32.6.3.6	s{6,4}
Snub hexaoctagonal tiling	32.6.3.8	sr{8,6}
Snub heptaheptagonal tiling	32.7.3.7	sr{7,7}
Snub octaoctagonal tiling	32.8.3.8	s{8,4}
Snub order-6 square tiling	33.4.3.4	s{4,6}
Snub apeiroapeirogonal tiling	32.∞.3.∞	sr{∞,∞}
Snub triheptagonal tiling	34.7	sr{7,3}
Snub trioctagonal tiling	34.8	sr{8,3}
Snub triapeirogonal tiling	34.∞	sr{∞,3}
Snub order-8 triangular tiling	35.4	s{3,8}
Order-7 triangular tiling	37	{3,7}
Order-8 triangular tiling	38	{3,8}
Infinite-order triangular tiling	3∞	{3,∞}
Alternated octagonal tiling	3.4.3.4.3.4	h{8,3}
Alternated order-4 hexagonal tiling	3.4.3.4.3.4.3.4	h{6,4}
Quarter order-6 square tiling	3.4.62.4	q{4,6}
Rhombitriheptagonal tiling	3.4.7.4	rr{7,3}
Rhombitrioctagonal tiling	3.4.8.4	rr{8,3}
Rhombitriapeirogonal tiling	3.4.∞.4	rr{∞,3}
Cantic octagonal tiling	3.6.4.6	h2{8,3}
Triheptagonal tiling	3.7.3.7	r{7,3}
Trioctagonal tiling	3.8.3.8	r{8,3}
Truncated heptagonal tiling	3.142	t{7,3}
Truncated octagonal tiling	3.162	t{8,3}
Triapeirogonal tiling	3.∞.3.∞	r{∞,3}
Truncated order-3 apeirogonal tiling	3.∞2	t{∞,3}
Rhombitetrapentagonal tiling	42.5.4	rr{5,4}
Rhombitetrahexagonal tiling	42.6.4	rr{6,4}
Rhombitetraheptagonal tiling	42.7.4	rr{7,4}
Rhombitetraoctagonal tiling	42.8.4	rr{8,4}
Rhombitetraapeirogonal tiling	42.∞.4	rr{∞,4}
Order-5 square tiling	45	{4,5}
Order-6 square tiling	46	{4,6}
Order-7 square tiling	47	{4,7}
Order-8 square tiling	48	{4,8}
Infinite-order square tiling	4∞	{4,∞}
Tetrapentagonal tiling	4.5.4.5	r{5,4}
Tetrahexagonal tiling	4.6.4.6	r{6,4}
Truncated trihexagonal tiling	4.6.12	tr{6,3}
Truncated triheptagonal tiling	4.6.14	tr{7,3}
Order 3-7 kisrhombille	V4.6.14	???
Truncated trioctagonal tiling	4.6.16	tr{8,3}
Order 3-8 kisrhombille	V4.6.16	???
Truncated triapeirogonal tiling	4.6.∞	tr{∞,3}
Tetraheptagonal tiling	4.7.4.7	r{7,4}
Tetraoctagonal tiling	4.8.4.8	r{8,4}
Truncated tetrapentagonal tiling	4.8.10	tr{5,4}
4-5 kisrhombille	V4.8.10	???
Truncated tetrahexagonal tiling	4.8.12	tr{6,4}
Truncated tetraheptagonal tiling	4.8.14	tr{7,4}
Truncated tetraoctagonal tiling	4.8.16	tr{8,4}
Truncated tetraapeirogonal tiling	4.8.∞	tr{∞,4}
Truncated order-4 pentagonal tiling	4.102	t{5,4}
Truncated pentahexagonal tiling	4.10.12	tr{6,5}
Truncated order-4 hexagonal tiling	4.122	t{6,4}
Truncated hexaoctagonal tiling	4.12.16	tr{8,6}
Truncated order-4 heptagonal tiling	4.142	t{7,4}
Truncated order-4 octagonal tiling	4.162	t{8,4}
Truncated order-4 apeirogonal tiling	4.∞2	t{∞,4}
Tetraapeirogonal tiling	4.∞.4.∞	r{∞,4}
Order-4 pentagonal tiling	54	{5,4}
Order-5 pentagonal tiling	55	{5,5}
Order-6 pentagonal tiling	56	{5,6}
Infinite-order pentagonal tiling	5∞	{5,∞}
Rhombipentahexagonal tiling	5.4.6.4	rr{6,5}
Pentahexagonal tiling	5.6.5.6	r{6,5}
Truncated order-5 square tiling	5.82	t{4,5}
Truncated order-5 pentagonal tiling	5.102	t{5,5}
Truncated order-5 hexagonal tiling	5.122	t{6,5}
Pentaapeirogonal tiling	5.∞.5.∞	r{∞,5}
Order-4 hexagonal tiling	64	{6,4}
Order-5 hexagonal tiling	65	{6,5}
Order-6 hexagonal tiling	66	{6,6}
Order-8 hexagonal tiling	68	{6,8}
Rhombihexaoctagonal tiling	6.4.8.4	rr{8,6}
Hexaoctagonal tiling	6.8.6.8	r{8,6}
Truncated order-6 square tiling	6.82	t{4,6}
Truncated order-6 pentagonal tiling	6.102	t{5,6}
Truncated order-6 hexagonal tiling	6.122	t{6,6}
Truncated order-6 octagonal tiling	6.162	t{8,6}
Heptagonal tiling	73	{7,3}
Order-4 heptagonal tiling	74	{7,4}
Order-7 heptagonal tiling	77	{7,7}
Truncated order-7 triangular tiling	7.62	t{3,7}
Truncated order-7 square tiling	7.82	t{4,7}
Truncated order-7 heptagonal tiling	7.142	t{7,7}
Octagonal tiling	83	{8,3}
Order-4 octagonal tiling	84	{8,4}
Order-6 octagonal tiling	86	{8,6}
Order-8 octagonal tiling	88	{8,8}
Truncated order-8 hexagonal tiling	812	t{6,8}
Truncated order-8 triangular tiling	8.62	t{3,8}
Truncated order-8 octagonal tiling	8.162	t{8,8}
Order-7 heptagrammic tiling	(7/2)7	{7/2,7}
Order-3 apeirogonal tiling	∞3	{∞,3}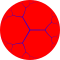
Order-4 apeirogonal tiling	∞4	{∞,4}
Order-5 apeirogonal tiling	∞5	{∞,5}
Infinite-order apeirogonal tiling	∞∞	{∞,∞}
Truncated infinite-order triangular tiling	∞.62	t{3,∞}
Truncated infinite-order square tiling	∞.82	t{4,∞}

See also

• Uniform tiling
  • Convex uniform honeycombs
  • List of k-uniform tilings
  • List of Euclidean uniform tilings
  • Uniform tilings in hyperbolic plane