Antiprism

Octagonal antiprism

In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies (not mirror images) of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.

Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron.

Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are 2n triangles, rather than n quadrilaterals.

The dual polyhedron of an n-gonal antiprism is an n-gonal trapezohedron.

History

In his 1619 book Harmonices Mundi , Johannes Kepler observed the existence of the infinite family of antiprisms. ^[1] This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net of a hexagonal antiprism has been attributed to Hieronymus Andreae, who died in 1556. ^[2]

The German form of the word "antiprism" was used for these shapes in the 19th century; Karl Heinze credits its introduction to Theodor Wittstein  [ de ]. ^[3] Although the English "anti-prism" had been used earlier for an optical prism used to cancel the effects of a primary optical element, ^[4] the first use of "antiprism" in English in its geometric sense appears to be in the early 20th century in the works of H. S. M. Coxeter. ^[5]

Special cases

Right antiprism

For an antiprism with regular n-gon bases, one usually considers the case where these two copies are twisted by an angle of ⁠180/n⁠ degrees.

The axis of a regular polygon is the line perpendicular to the polygon plane and lying in the polygon centre.

For an antiprism with congruent regularn-gon bases, twisted by an angle of ⁠180/n⁠ degrees, more regularity is obtained if the bases have the same axis: are coaxial ; i.e. (for non-coplanar bases): if the line connecting the base centers is perpendicular to the base planes. Then the antiprism is called a right antiprism, and its 2n side faces are isosceles triangles.

Uniform antiprism

A uniform n-antiprism has two congruent regular n-gons as base faces, and 2n equilateral triangles as side faces.

Uniform antiprisms, as do uniform prisms, form an infinite class of vertex-transitive polyhedra. For n = 2, one has the digonal antiprism (degenerate antiprism), which is visually identical to the regular tetrahedron; for n = 3, the regular octahedron as a triangular antiprism (non-degenerate antiprism).

Family of uniform n-gonal antiprisms

• v
• t
• e

Antiprism name	Digonal antiprism	(Trigonal) Triangular antiprism	(Tetragonal) Square antiprism	Pentagonal antiprism	Hexagonal antiprism	Heptagonal antiprism	...	Apeirogonal antiprism
Polyhedron image							...
Spherical tiling image							Plane tiling image
Vertex config.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3

The Schlegel diagrams of these semiregular antiprisms are as follows:

A3

A4

A5

A6

A7

A8

Cartesian coordinates

Cartesian coordinates for the vertices of a right n-antiprism (i.e. with regular n-gon bases and 2n isosceles triangle side faces, circumradius of the bases equal to 1) are:

${\displaystyle \left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)}$

where 0 ≤ k ≤ 2n – 1;

if the n-antiprism is uniform (i.e. if the triangles are equilateral), then: $${\displaystyle 2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.}$$

Volume and surface area

Let a be the edge-length of a uniform n-gonal antiprism; then the volume is: $${\displaystyle V={\frac {n{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}~a^{3},}$$

and the surface area is: $${\displaystyle A={\frac {n}{2}}\left(\cot {\frac {\pi }{n}}+{\sqrt {3}}\right)a^{2}.}$$

Furthermore, the volume of a regular right n-gonal antiprism with side length of its bases l and height h is given by: $${\displaystyle V={\frac {nhl^{2}}{12}}\left(\csc {\frac {\pi }{n}}+2\cot {\frac {\pi }{n}}\right).}$$

Derivation

The circumradius of the horizontal circumcircle of the regular ${\displaystyle n}$-gon at the base is

${\displaystyle R(0)={\frac {l}{2\sin {\frac {\pi }{n}}}}.}$

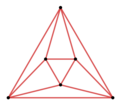
The vertices at the base are at

${\displaystyle \left({\begin{array}{c}R(0)\cos {\frac {2\pi m}{n}}\\R(0)\sin {\frac {2\pi m}{n}}\\0\end{array}}\right),\quad m=0..n-1;}$

the vertices at the top are at

${\displaystyle \left({\begin{array}{c}R(0)\cos {\frac {2\pi (m+1/2)}{n}}\\R(0)\sin {\frac {2\pi (m+1/2)}{n}}\\h\end{array}}\right),\quad m=0..n-1.}$

Via linear interpolation, points on the outer triangular edges of the antiprism that connect vertices at the bottom with vertices at the top are at

${\displaystyle \left({\begin{array}{c}{\frac {R(0)}{h}}[(h-z)\cos {\frac {2\pi m}{n}}+z\cos {\frac {\pi (2m+1)}{n}}]\\{\frac {R(0)}{h}}[(h-z)\sin {\frac {2\pi m}{n}}+z\sin {\frac {\pi (2m+1)}{n}}]\\\\z\end{array}}\right),\quad 0\leq z\leq h,m=0..n-1}$

and at

${\displaystyle \left({\begin{array}{c}{\frac {R(0)}{h}}[(h-z)\cos {\frac {2\pi (m+1)}{n}}+z\cos {\frac {\pi (2m+1)}{n}}]\\{\frac {R(0)}{h}}[(h-z)\sin {\frac {2\pi (m+1)}{n}}+z\sin {\frac {\pi (2m+1)}{n}}]\\\\z\end{array}}\right),\quad 0\leq z\leq h,m=0..n-1.}$

By building the sums of the squares of the ${\displaystyle x}$ and ${\displaystyle y}$ coordinates in one of the previous two vectors, the squared circumradius of this section at altitude ${\displaystyle z}$ is

${\displaystyle R(z)^{2}={\frac {R(0)^{2}}{h^{2}}}[h^{2}-2hz+2z^{2}+2z(h-z)\cos {\frac {\pi }{n}}].}$

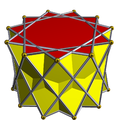
The horizontal section at altitude ${\displaystyle 0\leq z\leq h}$ above the base is a ${\displaystyle 2n}$-gon (truncated ${\displaystyle n}$-gon) with ${\displaystyle n}$ sides of length ${\displaystyle l_{1}(z)=l(1-z/h)}$ alternating with ${\displaystyle n}$ sides of length ${\displaystyle l_{2}(z)=lz/h}$. (These are derived from the length of the difference of the previous two vectors.) It can be dissected into ${\displaystyle n}$ isoceless triangles of edges ${\displaystyle R(z),R(z)}$ and ${\displaystyle l_{1}}$ (semiperimeter ${\displaystyle R(z)+l_{1}(z)/2}$) plus ${\displaystyle n}$ isoceless triangles of edges ${\displaystyle R(z),R(z)}$ and ${\displaystyle l_{2}(z)}$ (semiperimeter ${\displaystyle R(z)+l_{2}(z)/2}$). According to Heron's formula the areas of these triangles are

${\displaystyle Q_{1}(z)={\frac {R(0)^{2}}{h^{2}}}(h-z)\left[(h-z)\cos {\frac {\pi }{n}}+z\right]\sin {\frac {\pi }{n}}}$

and

${\displaystyle Q_{2}(z)={\frac {R(0)^{2}}{h^{2}}}z\left[z\cos {\frac {\pi }{n}}+h-z\right]\sin {\frac {\pi }{n}}.}$

The area of the section is ${\displaystyle n[Q_{1}(z)+Q_{2}(z)]}$, and the volume is

${\displaystyle V=n\int _{0}^{h}[Q_{1}(z)+Q_{2}(z)]dz={\frac {nh}{3}}R(0)^{2}\sin {\frac {\pi }{n}}(1+2\cos {\frac {\pi }{n}})={\frac {nh}{12}}l^{2}{\frac {1+2\cos {\frac {\pi }{n}}}{\sin {\frac {\pi }{n}}}}.}$

The volume of a right n-gonal prism with the same l and h is: $${\displaystyle V_{\mathrm {prism} }={\frac {nhl^{2}}{4}}\cot {\frac {\pi }{n}}}$$ which is smaller than that of an antiprism.

Symmetry

The symmetry group of a right n-antiprism (i.e. with regular bases and isosceles side faces) is D_nd = D_nv of order 4n, except in the cases of:

• n = 2: the regular tetrahedron, which has the larger symmetry group T_d of order 24 = 3 × (4 × 2), which has three versions of D_2d as subgroups;

• n = 3: the regular octahedron, which has the larger symmetry group O_h of order 48 = 4 × (4 × 3), which has four versions of D_3d as subgroups.

The symmetry group contains inversion if and only if n is odd.

The rotation group is D_n of order 2n, except in the cases of:

• n = 2: the regular tetrahedron, which has the larger rotation group T of order 12 = 3 × (2 × 2), which has three versions of D₂ as subgroups;

• n = 3: the regular octahedron, which has the larger rotation group O of order 24 = 4 × (2 × 3), which has four versions of D₃ as subgroups.

Note: The right n-antiprisms have congruent regular n-gon bases and congruent isosceles triangle side faces, thus have the same (dihedral) symmetry group as the uniform n-antiprism, for n ≥ 4.

Generalizations

In higher dimensions

Four-dimensional antiprisms can be defined as having two dual polyhedra as parallel opposite faces, so that each three-dimensional face between them comes from two dual parts of the polyhedra: a vertex and a dual polygon, or two dual edges. Every three-dimensional convex polyhedron is combinatorially equivalent to one of the two opposite faces of a four-dimensional antiprism, constructed from its canonical polyhedron and its polar dual. ^[6] However, there exist four-dimensional polychora that cannot be combined with their duals to form five-dimensional antiprisms. ^[7]

Self-crossing polyhedra

Further information: Prismatic uniform polyhedron

3/2-antiprism nonuniform	5/4-antiprism nonuniform	5/2-antiprism	5/3-antiprism
9/2-antiprism	9/4-antiprism	9/5-antiprism

All the non-star and star antiprisms up to 15 sides, together with those of a 29-gon (or icosaenneagon)

Uniform star antiprisms are named by their star polygon bases, {p/q}, and exist in prograde and in retrograde (crossed) solutions. Crossed forms have intersecting vertex figures, and are denoted by "inverted" fractions: p/(p – q) instead of p/q; example: 5/3 instead of 5/2.

A right star antiprism has two congruent coaxial regular convex or star polygon base faces, and 2n isosceles triangle side faces.

Any star antiprism with regular convex or star polygon bases can be made a right star antiprism (by translating and/or twisting one of its bases, if necessary).

In the retrograde forms, but not in the prograde forms, the triangles joining the convex or star bases intersect the axis of rotational symmetry. Thus:

• Retrograde star antiprisms with regular convex polygon bases cannot have all equal edge lengths, and so cannot be uniform. "Exception": a retrograde star antiprism with equilateral triangle bases (vertex configuration: 3.3/2.3.3) can be uniform; but then, it has the appearance of an equilateral triangle: it is a degenerate star polyhedron.

• Similarly, some retrograde star antiprisms with regular star polygon bases cannot have all equal edge lengths, and so cannot be uniform. Example: a retrograde star antiprism with regular star 7/5-gon bases (vertex configuration: 3.3.3.7/5) cannot be uniform.

Also, star antiprism compounds with regular star p/q-gon bases can be constructed if p and q have common factors. Example: a star 10/4-antiprism is the compound of two star 5/2-antiprisms.

Star p/q-antiprisms by symmetry, for p ≤ 12

Symmetry group	Uniform stars				Right stars
D4d [2+,8] (2*4)					3.3/2.3.4 Crossed square antiprism
D5h [2,5] (*225)	3.3.3.5/2 Pentagrammic antiprism				3.3/2.3.5 crossed pentagonal antiprism
D5d [2+,10] (2*5)	3.3.3.5/3 Pentagrammic crossed-antiprism
D6d [2+,12] (2*6)					3.3/2.3.6 crossed hexagonal antiprism
D7h [2,7] (*227)	3.3.3.7/2	3.3.3.7/4
D7d [2+,14] (2*7)	3.3.3.7/3
D8d [2+,16] (2*8)	3.3.3.8/3 Octagrammic antiprism	3.3.3.8/5 Octagrammic crossed-antiprism
D9h [2,9] (*229)	3.3.3.9/2 Enneagrammic antiprism (9/2)	3.3.3.9/4 Enneagrammic antiprism (9/4)
D9d [2+,18] (2*9)	3.3.3.9/5 Enneagrammic crossed-antiprism
D10d [2+,20] (2*10)	3.3.3.10/3 Decagrammic antiprism
D11h [2,11] (*2.2.11)	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
D11d [2+,22] (2*11)	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
D12d [2+,24] (2*12)	3.3.3.12/5	3.3.3.12/7
...	...

See also

• Grand antiprism, a four-dimensional polytope
• Skew polygon, a three-dimensional polygon whose convex hull is an antiprism

References

1. Kepler, Johannes (1619). "Book II, Definition X". Harmonices Mundi (in Latin). p. 49. See also illustration A, of a heptagonal antiprism.
2. Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (July 2008). "New light on the rediscovery of the Archimedean solids during the Renaissance". Archive for History of Exact Sciences. 62 (4): 457–467. doi:10.1007/s00407-008-0024-z. JSTOR   41134285.
3. Heinze, Karl (1886). Lucke, Franz (ed.). Genetische Stereometrie (in German). B. G. Teubner. p. 14.
4. Smyth, Piazzi (1881). "XVII. On the Constitution of the Lines forming the Low-Temperature Spectrum of Oxygen". Transactions of the Royal Society of Edinburgh. 30 (1): 419–425. doi:10.1017/s0080456800029112.
5. Coxeter, H. S. M. (January 1928). "The pure Archimedean polytopes in six and seven dimensions". Mathematical Proceedings of the Cambridge Philosophical Society. 24 (1): 1–9. Bibcode:1928PCPS...24....1C. doi:10.1017/s0305004100011786.
6. Grünbaum, Branko (2005). "Are prisms and antiprisms really boring? (Part 3)" (PDF). Geombinatorics. 15 (2): 69–78. MR   2298896.
7. Dobbins, Michael Gene (2017). "Antiprismlessness, or: reducing combinatorial equivalence to projective equivalence in realizability problems for polytopes". Discrete & Computational Geometry . 57 (4): 966–984. doi:10.1007/s00454-017-9874-y. MR   3639611.

Further reading

• Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN   0-520-03056-7. Chapter 2: Archimedean polyhedra, prisms and antiprisms

External links

• Media related to Antiprisms at Wikimedia Commons
• Weisstein, Eric W. "Antiprism". MathWorld .
• Nonconvex Prisms and Antiprisms
• Paper models of prisms and antiprisms