This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations .(March 2025) |
| Polyhedron | |
| Class | Number and properties |
|---|---|
| Platonic solids | (5, convex, regular) |
| Archimedean solids | (13, convex, uniform) |
| Kepler–Poinsot polyhedra | (4, regular, non-convex) |
| Uniform polyhedra | (75, uniform) |
| Prismatoid: prisms, antiprisms etc. | (4 infinite uniform classes) |
| Polyhedra tilings | (11 regular, in the plane) |
| Quasi-regular polyhedra | (8) |
| Johnson solids | (92, convex, non-uniform) |
| Bipyramids | (infinite) |
| Pyramids | (infinite) |
| Stellations | Stellations |
| Polyhedral compounds | (5 regular) |
| Deltahedra | (Deltahedra, equilateral triangle faces) |
| Snub polyhedra | (12 uniform, not mirror image) |
| Zonohedron | (Zonohedra, faces have 180°symmetry) |
| Dual polyhedron | |
| Self-dual polyhedron | (infinite) |
| Catalan solid | (13, Archimedean dual) |
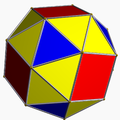
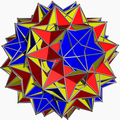
In geometry, a snub polyhedron is a polyhedron obtained by performing a snub operation: alternating a corresponding omnitruncated or truncated polyhedron, depending on the definition. Some, but not all, authors include antiprisms as snub polyhedra, as they are obtained by this construction from a degenerate "polyhedron" with only two faces (a dihedron).
Contents
Chiral snub polyhedra do not always have reflection symmetry and hence sometimes have two enantiomorphous (left- and right-handed) forms which are reflections of each other. Their symmetry groups are all point groups.
For example, the snub cube:
 |  |
Snub polyhedra have Wythoff symbol | p q r and by extension, vertex configuration 3.p.3.q.3.r. Retrosnub polyhedra (a subset of the snub polyhedron, containing the great icosahedron, small retrosnub icosicosidodecahedron, and great retrosnub icosidodecahedron) still have this form of Wythoff symbol, but their vertex configurations are instead