Small retrosnub icosicosidodecahedron

Last updated June 28, 2024

Small retrosnub icosicosidodecahedron

Type	Uniform star polyhedron
Elements	F = 112, E = 180 V = 60 (χ = −8)
Faces by sides	(40+60){3}+12{5/2}
Coxeter diagram
Wythoff symbol	\| 3/2 3/2 5/2
Symmetry group	I_h, [5,3], *532
Index references	U ₇₂, C ₉₁, W ₁₁₈
Dual polyhedron	Small hexagrammic hexecontahedron
Vertex figure	(3⁵.5/3)/2
Bowers acronym	Sirsid

In geometry, the small retrosnub icosicosidodecahedron (also known as a retrosnub disicosidodecahedron, small inverted retrosnub icosicosidodecahedron, or retroholosnub icosahedron) is a nonconvex uniform polyhedron, indexed as $U 72$ . It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices.^[1] It is given a Schläfli symbol sr{⁵/₃,³/₂}.

Convex hull

Its convex hull is a nonuniform truncated dodecahedron.

Truncated dodecahedron	Convex hull	Small retrosnub icosicosidodecahedron

Cartesian coordinates

Let $\xi =-{\frac {3}{2}}-{\frac {1}{2}}{\sqrt {1+4\phi }}\approx -2.866760399173862$ be the smallest (most negative) zero of the polynomial $P=x^{2}+3x+\phi ^{-2}$ , where $\phi$ is the golden ratio. Let the point $p$ be given by

p={\begin{pmatrix}\phi ^{-1}\xi +\phi ^{-3}\\\xi \\\phi ^{-2}\xi +\phi ^{-2}\end{pmatrix}}

.

Let the matrix $M$ be given by

M={\begin{pmatrix}1/2&-\phi /2&1/(2\phi )\\\phi /2&1/(2\phi )&-1/2\\1/(2\phi )&1/2&\phi /2\end{pmatrix}}

.

$M$ is the rotation around the axis $(1,0,\phi )$ by an angle of $2\pi /5$ , counterclockwise. Let the linear transformations $T_{0},\ldots ,T_{11}$ be the transformations which send a point $(x,y,z)$ to the even permutations of $(\pm x,\pm y,\pm z)$ with an even number of minus signs. The transformations $T_{i}$ constitute the group of rotational symmetries of a regular tetrahedron. The transformations $T_{i}M^{j}$ $(i=0,\ldots ,11$ , $j=0,\ldots ,4)$ constitute the group of rotational symmetries of a regular icosahedron. Then the 60 points $T_{i}M^{j}p$ are the vertices of a small snub icosicosidodecahedron. The edge length equals $-2\xi$ , the circumradius equals ${\sqrt {-4\xi -\phi ^{-2}}}$ , and the midradius equals ${\sqrt {-\xi }}$ .

For a small snub icosicosidodecahedron whose edge length is 1, the circumradius is

R={\frac {1}{2}}{\sqrt {\frac {\xi -1}{\xi }}}\approx 0.5806948001339209

Its midradius is

r={\frac {1}{2}}{\sqrt {\frac {-1}{\xi }}}\approx 0.2953073837589815

The other zero of $P$ plays a similar role in the description of the small snub icosicosidodecahedron.

Related Research Articles

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities $and with, is in a golden ratio to if$

In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space $under the operation of composition.$

<span class="mw-page-title-main">Snub dodecahedron</span> Archimedean solid with 92 faces

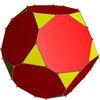
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.

In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).

<span class="mw-page-title-main">Pentagonal hexecontahedron</span>

In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images of each other. It has 92 vertices that span 60 pentagonal faces. It is the Catalan solid with the most vertices. Among the Catalan and Archimedean solids, it has the second largest number of vertices, after the truncated icosidodecahedron, which has 120 vertices.

In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two rotations is also a rotation. Therefore the set of rotations has a group structure, known as a rotation group.

In geometry, the great snub icosidodecahedron is a nonconvex uniform polyhedron, indexed as U₅₇. It has 92 faces (80 triangles and 12 pentagrams), 150 edges, and 60 vertices. It can be represented by a Schläfli symbol sr{5⁄2,3}, and Coxeter-Dynkin diagram .

In geometry, the small snub icosicosidodecahedron or snub disicosidodecahedron is a uniform star polyhedron, indexed as U₃₂. It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. Its stellation core is a truncated pentakis dodecahedron. It also called a holosnub icosahedron, $ß{3,5}.$

In geometry, the snub dodecadodecahedron is a nonconvex uniform polyhedron, indexed as $U 40$ . It has 84 faces (60 triangles, 12 pentagons, and 12 pentagrams), 150 edges, and 60 vertices. It is given a Schläfli symbol $sr{5 ⁄ 2,5},$ as a snub great dodecahedron.

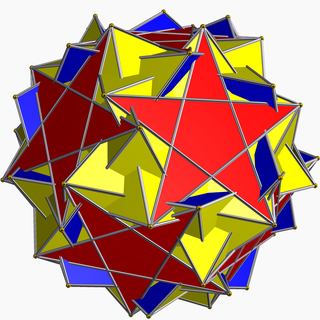
In geometry, the inverted snub dodecadodecahedron (or vertisnub dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U₆₀. It is given a Schläfli symbol $sr{5/3,5}.$

In geometry, the great inverted snub icosidodecahedron (or great vertisnub icosidodecahedron) is a uniform star polyhedron, indexed as U₆₉. It is given a Schläfli symbol $sr{5 ⁄ 3,3},$ and Coxeter-Dynkin diagram . In the book Polyhedron Models by Magnus Wenninger, the polyhedron is misnamed great snub icosidodecahedron, and vice versa.

In geometry, the snub icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U₄₆. It has 104 faces (80 triangles, 12 pentagons, and 12 pentagrams), 180 edges, and 60 vertices. As the name indicates, it belongs to the family of snub polyhedra.

In geometry, the great retrosnub icosidodecahedron or great inverted retrosnub icosidodecahedron is a nonconvex uniform polyhedron, indexed as $U 74$ . It has 92 faces (80 triangles and 12 pentagrams), 150 edges, and 60 vertices. It is given a Schläfli symbol $sr{3 ⁄ 2, 5 ⁄ 3}.$

Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius $in the x - y plane. Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length.$

In the Standard Model, using quantum field theory it is conventional to use the helicity basis to simplify calculations. In this basis, the spin is quantized along the axis in the direction of motion of the particle.

In mathematics, Liouville's formula, also known as the Abel–Jacobi–Liouville identity, is an equation that expresses the determinant of a square-matrix solution of a first-order system of homogeneous linear differential equations in terms of the sum of the diagonal coefficients of the system. The formula is named after the French mathematician Joseph Liouville. Jacobi's formula provides another representation of the same mathematical relationship.

In general relativity, a point mass deflects a light ray with impact parameter $by an angle approximately equal to$

In geometry, the small hexagrammic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the small retrosnub icosicosidodecahedron. It is partially degenerate, having coincident vertices, as its dual has coplanar triangular faces.

The uncertainty theory invented by Baoding Liu is a branch of mathematics based on normality, monotonicity, self-duality, countable subadditivity, and product measure axioms.

In mathematical analysis and its applications, a function of several real variables or real multivariate function is a function with more than one argument, with all arguments being real variables. This concept extends the idea of a function of a real variable to several variables. The "input" variables take real values, while the "output", also called the "value of the function", may be real or complex. However, the study of the complex-valued functions may be easily reduced to the study of the real-valued functions, by considering the real and imaginary parts of the complex function; therefore, unless explicitly specified, only real-valued functions will be considered in this article.

References

↑ Maeder, Roman. "72: small retrosnub icosicosidodecahedron". MathConsult.
↑ Birrell, Robert J. (May 1992). The Yog-sothoth: analysis and construction of the small inverted retrosnub icosicosidodecahedron (M.S.). California State University.
↑ Bowers, Jonathan (2000). "Uniform Polychora" (PDF). In Reza Sarhagi (ed.). Bridges 2000. Bridges Conference. pp. 239–246.

External links

Weisstein, Eric W. "Small retrosnub icosicosidodecahedron". MathWorld .
Klitzing, Richard. "3D star small retrosnub icosicosidodecahedron".

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Maeder, Roman. "72: small retrosnub icosicosidodecahedron". MathConsult.

[2] Birrell, Robert J. (May 1992). The Yog-sothoth: analysis and construction of the small inverted retrosnub icosicosidodecahedron (M.S.). California State University.

[3] Bowers, Jonathan (2000). "Uniform Polychora" (PDF). In Reza Sarhagi (ed.). Bridges 2000. Bridges Conference. pp. 239–246.

[1]

[2]

[3]