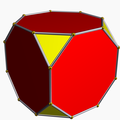
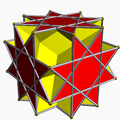
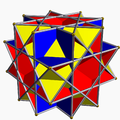
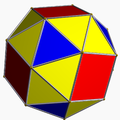
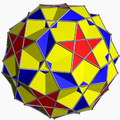
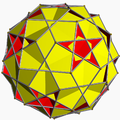
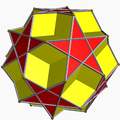
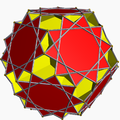
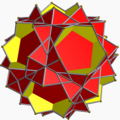
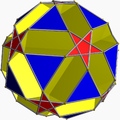
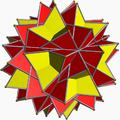
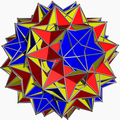
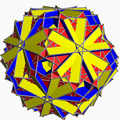
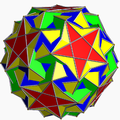
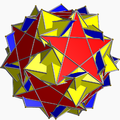
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both.
Contents
- Dihedral symmetry
- Tetrahedral symmetry
- Octahedral symmetry
- Icosahedral symmetry
- Degenerate cases
- Skilling's figure
- See also
- References
- External links
The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedra, 14 quasiregular ones, and 39 semiregular ones.
There are also two infinite sets of uniform star prisms and uniform star antiprisms.
Just as (nondegenerate) star polygons (which have polygon density greater than 1) correspond to circular polygons with overlapping tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhedra with overlapping tiles; there are 47 nonprismatic such uniform star polyhedra. The remaining 10 nonprismatic uniform star polyhedra, those that pass through the center, are the hemipolyhedra as well as Miller's monster, and do not have well-defined densities.
The nonconvex forms are constructed from Schwarz triangles.
All the uniform polyhedra are listed below by their symmetry groups and subgrouped by their vertex arrangements.
Regular polyhedra are labeled by their Schläfli symbol. Other nonregular uniform polyhedra are listed with their vertex configuration.
An additional figure, the pseudo great rhombicuboctahedron, is usually not included as a truly uniform star polytope, despite consisting of regular faces and having the same vertices.
Note: For nonconvex forms below an additional descriptor nonuniform is used when the convex hull vertex arrangement has same topology as one of these, but has nonregular faces. For example an nonuniform cantellated form may have rectangles created in place of the edges rather than squares.