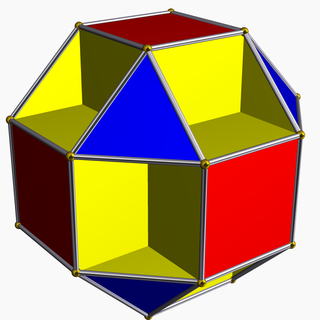
In geometry, an Archimedean solid is one of the 13 solids first enumerated by Archimedes. They are the convex uniform polyhedra composed of regular polygons meeting in identical vertices, excluding the five Platonic solids and excluding the prisms and antiprisms. They differ from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is the only radially equilateral convex polyhedron.
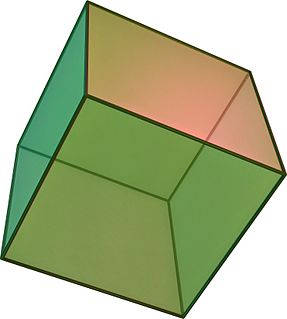
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.

In geometry, an octahedron is a polyhedron with eight faces, twelve edges, and six vertices. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each one. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.
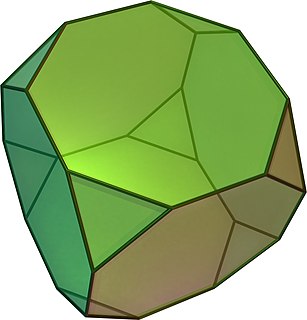
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex.

In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed. As such, the Klein quartic is the Hurwitz surface of lowest possible genus; see Hurwitz's automorphisms theorem. Its (orientation-preserving) automorphism group is isomorphic to PSL(2, 7), the second-smallest non-abelian simple group. The quartic was first described in.

A uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.
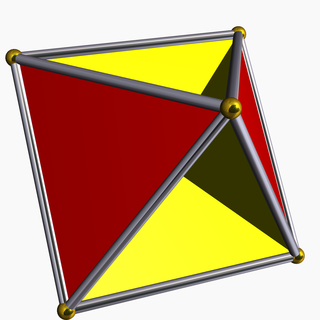
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 7 faces (4 triangles and 3 squares), 12 edges, and 6 vertices. Its vertex figure is a crossed quadrilateral. Its Coxeter–Dynkin diagram is (although this is a double covering of the tetrahemihexahedron).

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway calls this honeycomb a cubille.

In geometry, the heptagonal tiling is a regular tiling of the hyperbolic plane. It is represented by Schläfli symbol of {7,3}, having three regular heptagons around each vertex.

In geometry, the order-7 triangular tiling is a regular tiling of the hyperbolic plane with a Schläfli symbol of {3,7}.

In mathematics, a regular map is a symmetric tessellation of a closed surface. More precisely, a regular map is a decomposition of a two-dimensional manifold into topological disks such that every flag can be transformed into any other flag by a symmetry of the decomposition. Regular maps are, in a sense, topological generalizations of Platonic solids. The theory of maps and their classification is related to the theory of Riemann surfaces, hyperbolic geometry, and Galois theory. Regular maps are classified according to either: the genus and orientability of the supporting surface, the underlying graph, or the automorphism group.
In geometry, a (globally) projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids.
A pseudo-uniform polyhedron is a polyhedron which has regular polygons as faces and has the same vertex configuration at all vertices but is not vertex-transitive: it is not true that for any two vertices, there exists a symmetry of the polyhedron mapping the first isometrically onto the second. Thus, although all the vertices of a pseudo-uniform polyhedron appear the same, it is not isogonal. They are called pseudo-uniform polyhedra due to their resemblance to some true uniform polyhedra.

In geometry, the rhombitrioctagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one octagon, alternating between two squares. The tiling has Schläfli symbol rr{8,3}. It can be seen as constructed as a rectified trioctagonal tiling, r{8,3}, as well as an expanded octagonal tiling or expanded order-8 triangular tiling.

In the geometry of hyperbolic 3-space, the square tiling honeycomb is one of 11 paracompact regular honeycombs. It is called paracompact because it has infinite cells, whose vertices exist on horospheres and converge to a single ideal point at infinity. Given by Schläfli symbol {4,4,3}, it has three square tilings, {4,4}, around each edge, and six square tilings around each vertex, in a cubic {4,3} vertex figure.