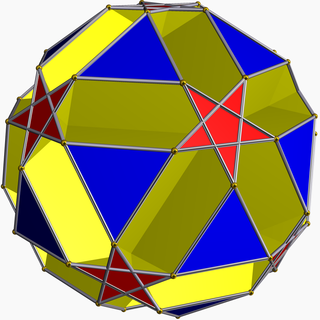
In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.

In geometry, the great ditrigonal icosidodecahedron (or great ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U47. It has 32 faces (20 triangles and 12 pentagons), 60 edges, and 20 vertices. It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 | 3 5⁄4 gives Coxeter diagram = . It has extended Schläfli symbol a{5⁄2,3} or c{3,5⁄2}, as an altered great stellated dodecahedron or converted great icosahedron.
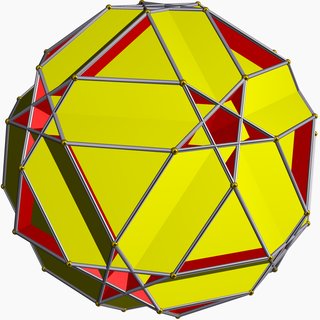
In geometry, the small dodecicosahedron (or small dodekicosahedron) is a nonconvex uniform polyhedron, indexed as U50. It has 32 faces (20 hexagons and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the small dodecicosidodecahedron (or small dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U33. It has 44 faces (20 triangles, 12 pentagons, and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great icosicosidodecahedron (or great icosified icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U48. It has 52 faces (20 triangles, 12 pentagrams, and 20 hexagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the small rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U39. It has 42 faces (30 squares and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the small ditrigonal icosidodecahedron (or small ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U30. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol a{5,3}, as an altered dodecahedron, and Coxeter diagram or .

In geometry, the truncated great dodecahedron is a nonconvex uniform polyhedron, indexed as U37. It has 24 faces (12 pentagrams and 12 decagons), 90 edges, and 60 vertices. It is given a Schläfli symbol t{5,5/2}.
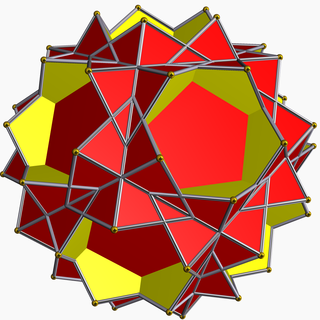
In geometry, the small stellated truncated dodecahedron (or quasitruncated small stellated dodecahedron or small stellatruncated dodecahedron) is a nonconvex uniform polyhedron, indexed as U58. It has 24 faces (12 pentagons and 12 decagrams), 90 edges, and 60 vertices. It is given a Schläfli symbol t{5⁄3,5}, and Coxeter diagram .

In geometry, the great stellated truncated dodecahedron (or quasitruncated great stellated dodecahedron or great stellatruncated dodecahedron) is a nonconvex uniform polyhedron, indexed as U66. It has 32 faces (20 triangles and 12 decagrams), 90 edges, and 60 vertices. It is given a Schläfli symbol t0,1{5/3,3}.

In geometry, the great ditrigonal dodecicosidodecahedron (or great dodekified icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U42. It has 44 faces (20 triangles, 12 pentagons, and 12 decagrams), 120 edges, and 60 vertices. Its vertex figure is an isosceles trapezoid.

In geometry, the great dodecicosidodecahedron (or great dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U61. It has 44 faces (20 triangles, 12 pentagrams and 12 decagrams), 120 edges and 60 vertices.
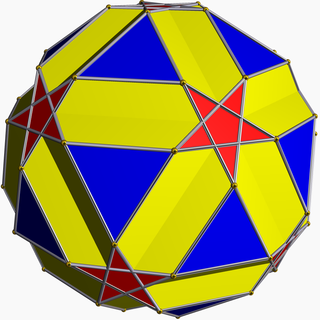
In geometry, the small icosicosidodecahedron (or small icosified icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U31. It has 52 faces (20 triangles, 12 pentagrams, and 20 hexagons), 120 edges, and 60 vertices.

In geometry, the ditrigonal dodecadodecahedron (or ditrigonary dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U41. It has 24 faces (12 pentagons and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol b{5,5⁄2}, as a blended great dodecahedron, and Coxeter diagram . It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 | 5⁄3 5, and Coxeter diagram .

In geometry, the nonconvex great rhombicosidodecahedron is a nonconvex uniform polyhedron, indexed as U67. It has 62 faces (20 triangles, 30 squares and 12 pentagrams), 120 edges, and 60 vertices. It is also called the quasirhombicosidodecahedron. It is given a Schläfli symbol rr{5⁄3,3}. Its vertex figure is a crossed quadrilateral.

In geometry, the great dodecicosahedron (or great dodekicosahedron) is a nonconvex uniform polyhedron, indexed as U63. It has 32 faces (20 hexagons and 12 decagrams), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.
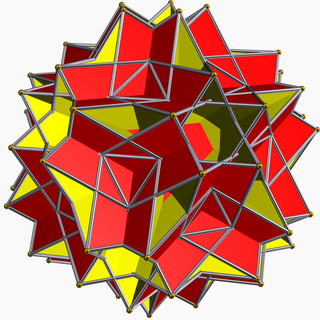
In geometry, the great rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U73. It has 42 faces (30 squares, 12 decagrams), 120 edges and 60 vertices. Its vertex figure is a crossed quadrilateral.

The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876.

In geometry, the small ditrigonal dodecacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small ditrigonal dodecicosidodecahedron. It is visually identical to the small dodecicosacron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models.
In geometry, there are seven uniform and uniform dual polyhedra named as ditrigonal.