In geometry, a dodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.
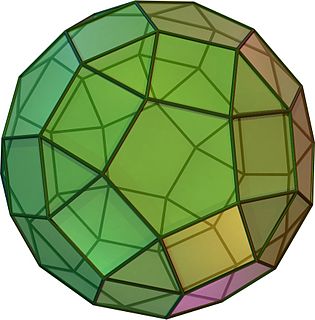
In geometry, the rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.
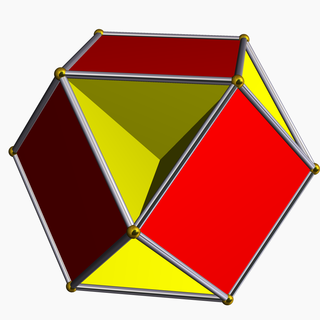
In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. It has 10 faces (6 squares and 4 regular hexagons), 24 edges and 12 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the small icosihemidodecahedron (or small icosahemidodecahedron) is a uniform star polyhedron, indexed as U49. It has 26 faces (20 triangles and 6 decagons), 60 edges, and 30 vertices. Its vertex figure alternates two regular triangles and decagons as a crossed quadrilateral.
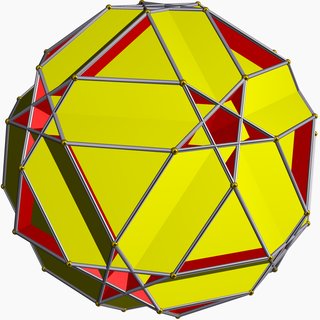
In geometry, the small dodecicosahedron (or small dodekicosahedron) is a nonconvex uniform polyhedron, indexed as U50. It has 32 faces (20 hexagons and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the octahemioctahedron or allelotetratetrahedron is a nonconvex uniform polyhedron, indexed as U3. It has 12 faces (8 triangles and 4 hexagons), 24 edges and 12 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the rhombicosahedron is a nonconvex uniform polyhedron, indexed as U56. It has 50 faces (30 squares and 20 hexagons), 120 edges and 60 vertices. Its vertex figure is an antiparallelogram.

In geometry, the great icosicosidodecahedron (or great icosified icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U48. It has 52 faces (20 triangles, 12 pentagrams, and 20 hexagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the small rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U39. It has 42 faces (30 squares and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the small ditrigonal icosidodecahedron (or small ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U30. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol a{5,3}, as an altered dodecahedron, and Coxeter diagram or .
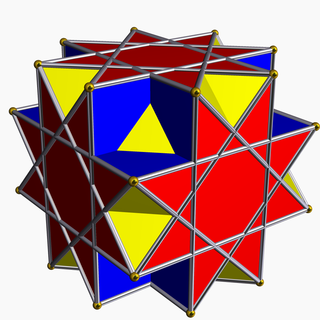
In geometry, the great cubicuboctahedron is a nonconvex uniform polyhedron, indexed as U14. It has 20 faces (8 triangles, 6 squares and 6 octagrams), 18 edges, and 24 vertices. Its square faces and its octagrammic faces are parallel to those of a cube, while its triangular faces are parallel to those of an octahedron: hence the name cubicuboctahedron. The great suffix serves to distinguish it from the small cubicuboctahedron, which also has faces in the aforementioned directions.
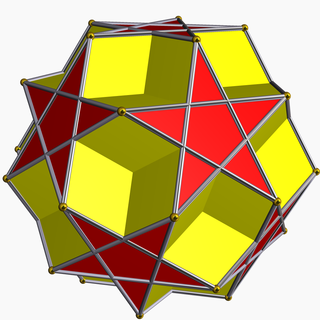
In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U36. It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

In geometry, the great stellated truncated dodecahedron (or quasitruncated great stellated dodecahedron or great stellatruncated dodecahedron) is a nonconvex uniform polyhedron, indexed as U66. It has 32 faces (20 triangles and 12 pentagrams), 90 edges, and 60 vertices. It is given a Schläfli symbol t0,1{5/3,3}.

In geometry, the small dodecahemicosahedron (or great dodecahemiicosahedron) is a nonconvex uniform polyhedron, indexed as U62. It has 22 faces (12 pentagrams and 10 hexagons), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great dodecahemicosahedron (or small dodecahemiicosahedron) is a nonconvex uniform polyhedron, indexed as U65. It has 22 faces (12 pentagons and 10 hexagons), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the icosidodecadodecahedron (or icosified dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U44. It has 44 faces (12 pentagons, 12 pentagrams and 20 hexagons), 120 edges and 60 vertices. Its vertex figure is a crossed quadrilateral.
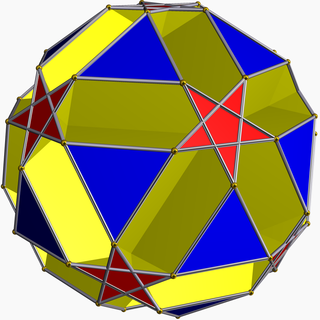
In geometry, the small ditrigonal dodecicosidodecahedron (or small dodekified icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U43. It has 44 faces (20 triangles, 12 pentagrams and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great dodecicosahedron (or great dodekicosahedron) is a nonconvex uniform polyhedron, indexed as U63. It has 32 faces (20 hexagons and 12 decagrams), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

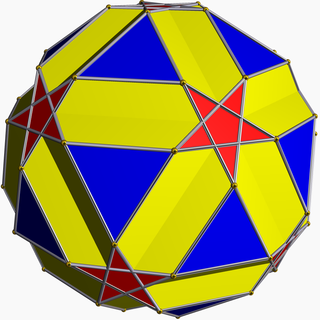
In geometry, the small retrosnub icosicosidodecahedron (also known as a retrosnub disicosidodecahedron, small inverted retrosnub icosicosidodecahedron, or retroholosnub icosahedron) is a nonconvex uniform polyhedron, indexed as U72. It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. It is given a Schläfli symbol ß{3⁄2,5}.