In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron or omnitruncated icosahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.

In geometry, the hexagonal prism is a prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 faces, 18 edges, and 12 vertices.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .
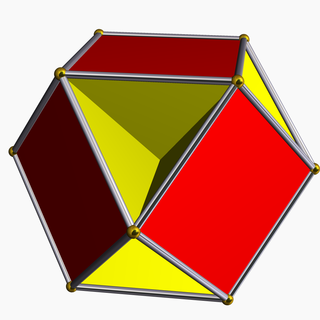
In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. It has 10 faces (6 squares and 4 regular hexagons), 24 edges and 12 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the octahemioctahedron or allelotetratetrahedron is a nonconvex uniform polyhedron, indexed as U3. It has 12 faces (8 triangles and 4 hexagons), 24 edges and 12 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the rhombicosahedron is a nonconvex uniform polyhedron, indexed as U56. It has 50 faces (30 squares and 20 hexagons), 120 edges and 60 vertices. Its vertex figure is an antiparallelogram.

In geometry, the small ditrigonal icosidodecahedron (or small ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U30. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol a{5,3}, as an altered dodecahedron, and Coxeter diagram or .
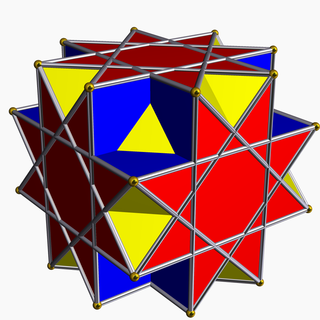
In geometry, the great cubicuboctahedron is a nonconvex uniform polyhedron, indexed as U14. It has 20 faces (8 triangles, 6 squares and 6 octagrams), 48 edges, and 24 vertices. Its square faces and its octagrammic faces are parallel to those of a cube, while its triangular faces are parallel to those of an octahedron: hence the name cubicuboctahedron. The great suffix serves to distinguish it from the small cubicuboctahedron, which also has faces in the aforementioned directions.
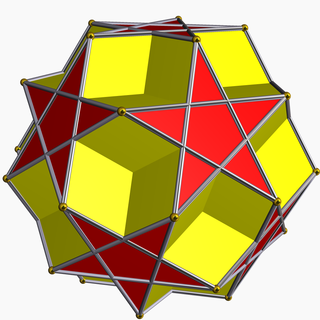
In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U36. It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

In geometry, the small icosicosidodecahedron (or small icosified icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U31. It has 52 faces (20 triangles, 12 pentagrams, and 20 hexagons), 120 edges, and 60 vertices.
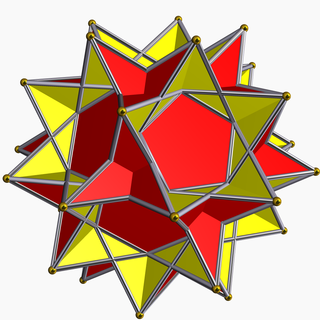
In geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. It has 18 faces (12 pentagrams and 6 decagrams), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great dodecahemicosahedron (or small dodecahemiicosahedron) is a nonconvex uniform polyhedron, indexed as U65. It has 22 faces (12 pentagons and 10 hexagons), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the icosidodecadodecahedron (or icosified dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U44. It has 44 faces (12 pentagons, 12 pentagrams and 20 hexagons), 120 edges and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the nonconvex great rhombicosidodecahedron is a nonconvex uniform polyhedron, indexed as U67. It has 62 faces (20 triangles, 30 squares and 12 pentagrams), 120 edges, and 60 vertices. It is also called the quasirhombicosidodecahedron. It is given a Schläfli symbol rr{5⁄3,3}. Its vertex figure is a crossed quadrilateral.
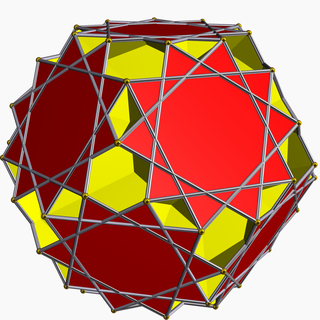
In geometry, the great dodecicosahedron (or great dodekicosahedron) is a nonconvex uniform polyhedron, indexed as U63. It has 32 faces (20 hexagons and 12 decagrams), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, faceting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.
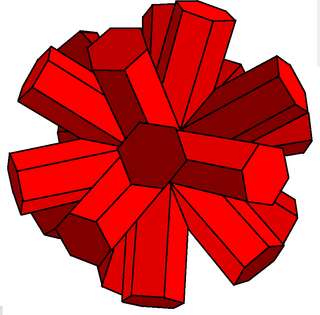
In geometry, the small dodecahemicosacron is the dual of the small dodecahemicosahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the great dodecahemicosacron.