In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.

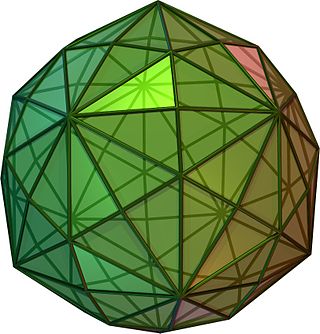
In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.

In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.
In geometry, the rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron.

In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.

In geometry, a disdyakis dodecahedron,, is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it. More formally, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron. The net of the rhombic dodecahedral pyramid also shares the same topology.
In geometry, a disdyakis triacontahedron, hexakis icosahedron, decakis dodecahedron or kisrhombic triacontahedron is a Catalan solid with 120 faces and the dual to the Archimedean truncated icosidodecahedron. As such it is face-uniform but with irregular face polygons. It slightly resembles an inflated rhombic triacontahedron: if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion, one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It also has the most faces among the Archimedean and Catalan solids, with the snub dodecahedron, with 92 faces, in second place.

In geometry, the great truncated icosidodecahedron (or great quasitruncated icosidodecahedron or stellatruncated icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U68. It has 62 faces (30 squares, 20 hexagons, and 12 decagrams), 180 edges, and 120 vertices. It is given a Schläfli symbol t0,1,2{5⁄3,3}, and Coxeter-Dynkin diagram, .

In geometry, the great snub icosidodecahedron is a nonconvex uniform polyhedron, indexed as U57. It has 92 faces (80 triangles and 12 pentagrams), 150 edges, and 60 vertices. It can be represented by a Schläfli symbol sr{5⁄2,3}, and Coxeter-Dynkin diagram .
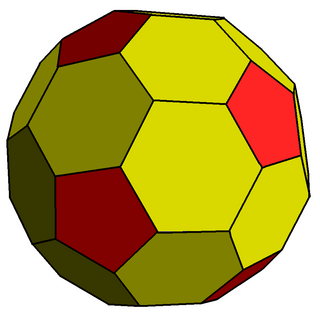
In geometry, the chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.

A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals. It is represented by the Schläfli symbol {5,3}.

In geometry, the medial rhombic triacontahedron is a nonconvex isohedral polyhedron. It is a stellation of the rhombic triacontahedron, and can also be called small stellated triacontahedron. Its dual is the dodecadodecahedron.

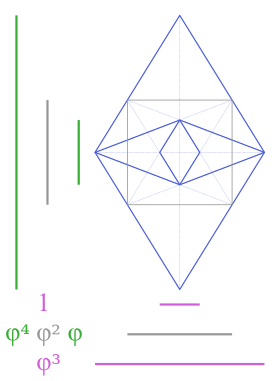
In geometry, a golden rhombus is a rhombus whose diagonals are in the golden ratio:

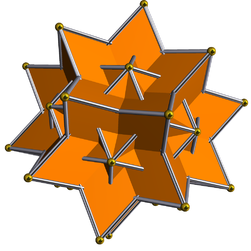
In geometry, the great triambic icosahedron and medial triambic icosahedron (or midly triambic icosahedron) are visually identical dual uniform polyhedra. The exterior surface also represents the De2f2 stellation of the icosahedron. These figures can be differentiated by marking which intersections between edges are true vertices and which are not. In the above images, true vertices are marked by gold spheres, which can be seen in the concave Y-shaped areas. Alternatively, if the faces are filled with the even–odd rule, the internal structure of both shapes will differ.

In geometry, the great rhombihexacron (or great dipteral disdodecahedron) is a nonconvex isohedral polyhedron. It is the dual of the uniform great rhombihexahedron (U21). It has 24 identical bow-tie-shaped faces, 18 vertices, and 48 edges.

In geometry, the great stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great icosahedron. It has 60 intersecting triangular faces.

In geometry, the small hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small snub icosicosidodecahedron. It is partially degenerate, having coincident vertices, as its dual has coplanar triangular faces.

In geometry, the great pentakis dodecahedron is a nonconvex isohedral polyhedron.

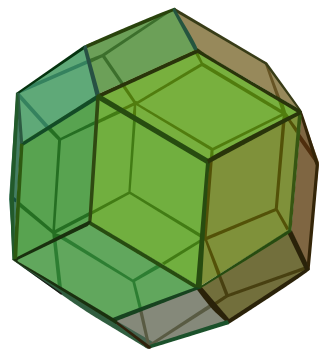
In geometry, the Bilinski dodecahedron is a convex polyhedron with twelve congruent golden rhombus faces. It has the same topology but a different geometry than the face-transitive rhombic dodecahedron. It is a parallelohedron.