
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.
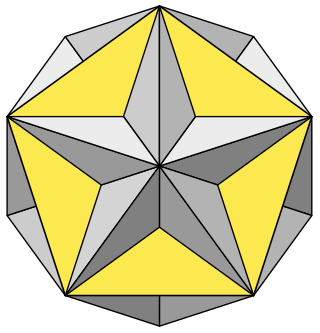
In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra.

In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in n dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word stellation comes from the Latin stellātus, "starred", which in turn comes from Latin stella, "star". Stellation is the reciprocal or dual process to faceting.
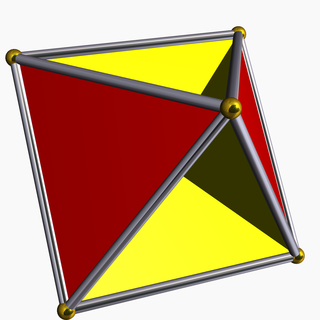
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 7 faces (4 triangles and 3 squares), 12 edges, and 6 vertices. Its vertex figure is a crossed quadrilateral. Its Coxeter–Dynkin diagram is (although this is a double covering of the tetrahemihexahedron).

In geometry, the complete or final stellation of the icosahedron is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram. That is, every three intersecting face planes of the icosahedral core intersect either on a vertex of this polyhedron, or inside of it.

In geometry, the great stellated dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5⁄2,3}. It is one of four nonconvex regular polyhedra.
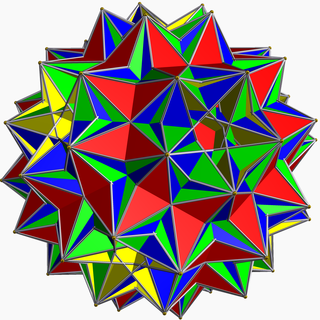
In geometry, the great disnub dirhombidodecahedron, also called Skilling's figure, is a degenerate uniform star polyhedron.
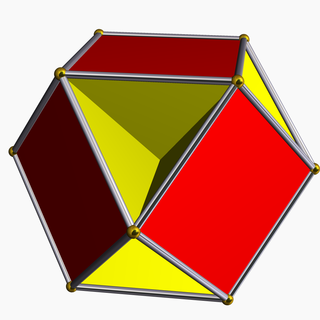
In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. It has 10 faces (6 squares and 4 regular hexagons), 24 edges and 12 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the octahemioctahedron or allelotetratetrahedron is a nonconvex uniform polyhedron, indexed as U3. It has 12 faces (8 triangles and 4 hexagons), 24 edges and 12 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great dodecahemicosahedron (or small dodecahemiicosahedron) is a nonconvex uniform polyhedron, indexed as U65. It has 22 faces (12 pentagons and 10 hexagons), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.
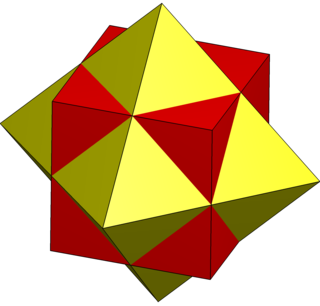
The compound of cube and octahedron is a polyhedron which can be seen as either a polyhedral stellation or a compound.

In geometry, the small triambic icosahedron is a star polyhedron composed of 20 intersecting non-regular hexagon faces. It has 60 edges and 32 vertices, and Euler characteristic of −8. It is an isohedron, meaning that all of its faces are symmetric to each other. Branko Grünbaum has conjectured that it is the only Euclidean isohedron with convex faces of six or more sides, but the small hexagonal hexecontahedron is another example.

In geometry, the great triambic icosahedron and medial triambic icosahedron (or midly triambic icosahedron) are visually identical dual uniform polyhedra. The exterior surface also represents the De2f2 stellation of the icosahedron. These figures can be differentiated by marking which intersections between edges are true vertices and which are not. In the above images, true vertices are marked by gold spheres, which can be seen in the concave Y-shaped areas. Alternatively, if the faces are filled with the even–odd rule, the internal structure of both shapes will differ.

In geometry, the small dodecahemidodecacron is the dual of the small dodecahemidodecahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the small icosihemidodecacron.

In geometry, the small icosihemidodecacron is the dual of the small icosihemidodecahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the small dodecahemidodecacron.
In geometry, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron – hence the "hemi" prefix.
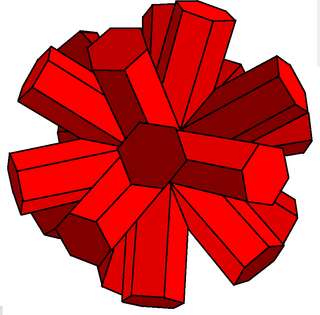
In geometry, the small dodecahemicosacron is the dual of the small dodecahemicosahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the great dodecahemicosacron.

In geometry, the great dodecahemidodecacron is the dual of the great dodecahemidodecahedron, and is one of nine dual hemipolyhedra. It appears indistinct from the great icosihemidodecacron.

In geometry, the great dirhombicosidodecacron is a nonconvex isohedral polyhedron. It is the dual of the great dirhombicosidodecahedron.

















