In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.

In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5⁄2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.
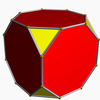
In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. It has 10 faces (6 squares and 4 regular hexagons), 24 edges and 12 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the small rhombihexahedron (or small rhombicube) is a nonconvex uniform polyhedron, indexed as U18. It has 18 faces (12 squares and 6 octagons), 48 edges, and 24 vertices. Its vertex figure is an antiparallelogram.

In geometry, the rhombicosahedron is a nonconvex uniform polyhedron, indexed as U56. It has 50 faces (30 squares and 20 hexagons), 120 edges and 60 vertices. Its vertex figure is an antiparallelogram.

In geometry, the small rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U39. It has 42 faces (30 squares and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.
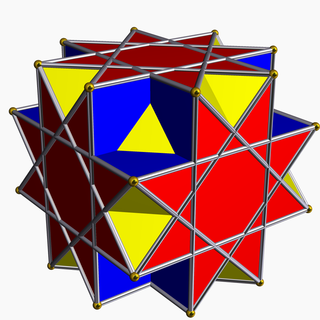
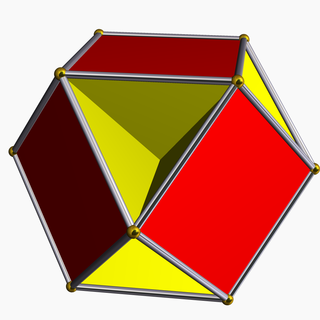
In geometry, the great cubicuboctahedron is a nonconvex uniform polyhedron, indexed as U14. It has 20 faces (8 triangles, 6 squares and 6 octagrams), 48 edges, and 24 vertices. Its square faces and its octagrammic faces are parallel to those of a cube, while its triangular faces are parallel to those of an octahedron: hence the name cubicuboctahedron. The prefix great serves to distinguish it from the small cubicuboctahedron, which also has faces in the aforementioned directions.

In geometry, the great icosidodecahedron is a nonconvex uniform polyhedron, indexed as U54. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 30 vertices. It is given a Schläfli symbol r{3,5⁄2}. It is the rectification of the great stellated dodecahedron and the great icosahedron. It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

In geometry, the truncated great dodecahedron is a nonconvex uniform polyhedron, indexed as U37. It has 24 faces (12 pentagrams and 12 decagons), 90 edges, and 60 vertices. It is given a Schläfli symbol t{5,5/2}.

In geometry, the rhombidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U38. It has 54 faces (30 squares, 12 pentagons and 12 pentagrams), 120 edges and 60 vertices. It is given a Schläfli symbol t0,2{5⁄2,5}, and by the Wythoff construction this polyhedron can also be named a cantellated great dodecahedron.
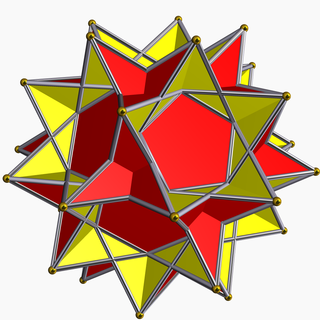
In geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. It has 18 faces (12 pentagrams and 6 decagrams), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great dodecahemicosahedron (or great dodecahemiicosahedron) is a nonconvex uniform polyhedron, indexed as U65. It has 22 faces (12 pentagons and 10 hexagons), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the nonconvex great rhombicosidodecahedron is a nonconvex uniform polyhedron, indexed as U67. It has 62 faces (20 triangles, 30 squares and 12 pentagrams), 120 edges, and 60 vertices. It is also called the quasirhombicosidodecahedron. It is given a Schläfli symbol rr{5⁄3,3}. Its vertex figure is a crossed quadrilateral.
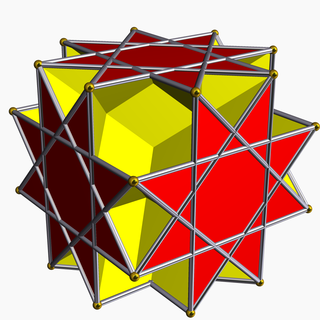
In geometry, the great rhombihexahedron (or great rhombicube) is a nonconvex uniform polyhedron, indexed as U21. It has 18 faces (12 squares and 6 octagrams), 48 edges, and 24 vertices. Its dual is the great rhombihexacron. Its vertex figure is a crossed quadrilateral.
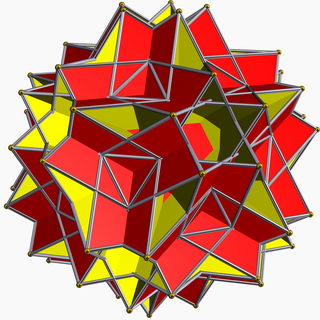
In geometry, the great rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U73. It has 42 faces (30 squares, 12 decagrams), 120 edges and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both.
A pseudo-uniform polyhedron is a polyhedron which has regular polygons as faces and has the same vertex configuration at all vertices but is not vertex-transitive: it is not true that for any two vertices, there exists a symmetry of the polyhedron mapping the first isometrically onto the second. Thus, although all the vertices of a pseudo-uniform polyhedron appear the same, it is not isogonal. They are called pseudo-uniform polyhedra due to their resemblance to some true uniform polyhedra.
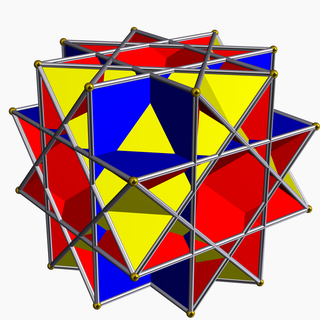


![]()
![]()
![]()
![]()
![]()
![]()
![]() . Its vertex figure is a crossed quadrilateral.
. Its vertex figure is a crossed quadrilateral.