
In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.

In geometry, the deltoidal icositetrahedron is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.

In geometry, a pentagonal icositetrahedron or pentagonal icosikaitetrahedron is a Catalan solid which is the dual of the snub cube. In crystallography it is also called a gyroid.

In geometry, the small dodecicosidodecahedron (or small dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U33. It has 44 faces (20 triangles, 12 pentagons, and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.
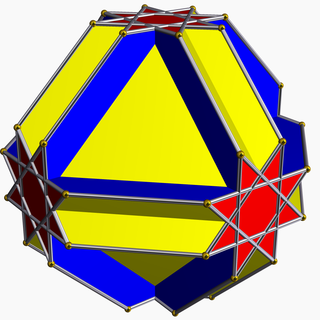
In geometry, the cubitruncated cuboctahedron or cuboctatruncated cuboctahedron is a nonconvex uniform polyhedron, indexed as U16. It has 20 faces (8 hexagons, 6 octagons, and 6 octagrams), 72 edges, and 48 vertices,and has a shäfli symbol of tr{4,3/2}
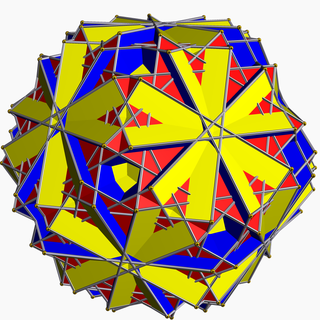
In geometry, the great truncated icosidodecahedron (or great quasitruncated icosidodecahedron or stellatruncated icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U68. It has 62 faces (30 squares, 20 hexagons, and 12 decagrams), 180 edges, and 120 vertices. It is given a Schläfli symbol t0,1,2{5⁄3,3}, and Coxeter-Dynkin diagram, .

In geometry, the great dodecicosacron (or great dipteral trisicosahedron) is the dual of the great dodecicosahedron (U63). It has 60 intersecting bow-tie-shaped faces.

In geometry, the great hexacronic icositetrahedron is the dual of the great cubicuboctahedron. Its faces are kites. Part of each kite lies inside the solid, hence is invisible in solid models.

In geometry, the small rhombihexacron is the dual of the small rhombihexahedron. It is visually identical to the small hexacronic icositetrahedron. Its faces are antiparallelograms formed by pairs of coplanar triangles.

In geometry, the small hexacronic icositetrahedron is the dual of the small cubicuboctahedron. It is visually identical to the small rhombihexacron. A part of each dart lies inside the solid, hence is invisible in solid models.

In geometry, the small rhombidodecacron is a nonconvex isohedral polyhedron. It is the dual of the small rhombidodecahedron. It is visually identical to the Small dodecacronic hexecontahedron. It has 60 intersecting antiparallelogram faces.

In geometry, the great icosacronic hexecontahedron is the dual of the great icosicosidodecahedron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models.

In geometry, the great triakis octahedron is the dual of the stellated truncated hexahedron (U19). It has 24 intersecting isosceles triangle faces. Part of each triangle lies within the solid, hence is invisible in solid models.

In geometry, the great rhombihexacron (or great dipteral disdodecahedron) is a nonconvex isohedral polyhedron. It is the dual of the uniform great rhombihexahedron (U21). It has 24 identical bow-tie-shaped faces, 18 vertices, and 48 edges.

In geometry, the medial deltoidal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the rhombidodecadodecahedron. Its 60 intersecting quadrilateral faces are kites.

In geometry, the great deltoidal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the nonconvex great rhombicosidodecahedron. It is visually identical to the great rhombidodecacron. It has 60 intersecting cross quadrilateral faces, 120 edges, and 62 vertices. Its faces are darts. Part of each dart lies inside the solid, hence is invisible in solid models.

In geometry, the great rhombidodecacron is a nonconvex isohedral polyhedron. It is the dual of the great rhombidodecahedron. It is visually identical to the great deltoidal hexecontahedron. Its faces are antiparallelograms.

In geometry, the great disdyakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great truncated cuboctahedron. It has 48 triangular faces.

In geometry, the great ditrigonal dodecacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great ditrigonal dodecicosidodecahedron. Its faces are kites. Part of each kite lies inside the solid, hence is invisible in solid models.

In geometry, the small ditrigonal dodecacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small ditrigonal dodecicosidodecahedron. It is visually identical to the small dodecicosacron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models.

























