
In geometry, an Archimedean solid is one of 13 convex polyhedra whose faces are regular polygons and whose vertices are all symmetric to each other. They were first enumerated by Archimedes. They belong to the class of convex uniform polyhedra, the convex polyhedra with regular faces and symmetric vertices, which is divided into the Archimedean solids, the five Platonic solids, and the two infinite families of prisms and antiprisms. The pseudorhombicuboctahedron is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive. An even larger class than the convex uniform polyhedra is the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices.

In geometry, rhombicuboctahedron is an Archimedean solid with 26 faces, consisting of 8 equilateral triangles and 18 squares. It is named by Johannes Kepler in his 1618 Harmonices Mundi, being short for truncated cuboctahedral rhombus, with cuboctahedral rhombus being his name for a rhombic dodecahedron.

In geometry, a decagon is a ten-sided polygon or 10-gon. The total sum of the interior angles of a simple decagon is 1440°.

In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol {3,3,3}. It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It is the 4-simplex (Coxeter's polytope), the simplest possible convex 4-polytope, and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The 5-cell is a 4-dimensional pyramid with a tetrahedral base and four tetrahedral sides.

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.

In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,4}. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid [sic?].

In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron, is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.

In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.

In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.

In geometry, the deltoidal icositetrahedron is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.

In geometry, a deltoidal hexecontahedron is a Catalan solid which is the dual polyhedron of the rhombicosidodecahedron, an Archimedean solid. It is one of six Catalan solids to not have a Hamiltonian path among its vertices.

In geometry, a pentagonal icositetrahedron or pentagonal icosikaitetrahedron is a Catalan solid which is the dual of the snub cube. In crystallography it is also called a gyroid.

In geometry, the snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex. It has Schläfli symbol sr{3,6}. The snub tetrahexagonal tiling is a related hyperbolic tiling with Schläfli symbol sr{4,6}.

In geometry, a truncated 24-cell is a uniform 4-polytope formed as the truncation of the regular 24-cell.
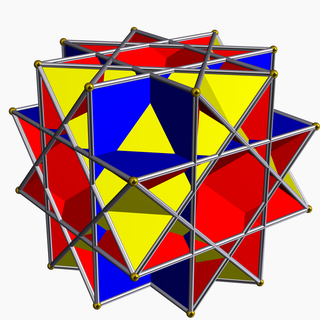
In geometry, the nonconvex great rhombicuboctahedron is a nonconvex uniform polyhedron, indexed as U17. It has 26 faces (8 triangles and 18 squares), 48 edges, and 24 vertices. It is represented by the Schläfli symbol rr{4,3⁄2} and Coxeter-Dynkin diagram of . Its vertex figure is a crossed quadrilateral.

In geometry, a tessellation of dimension 2 or higher, or a polytope of dimension 3 or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent but must be transitive, i.e. must lie within the same symmetry orbit. In other words, for any two faces A and B, there must be a symmetry of the entire figure by translations, rotations, and/or reflections that maps A onto B. For this reason, convex isohedral polyhedra are the shapes that will make fair dice.
In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos−1(1/5), or approximately 78.46°.

In geometry, the great deltoidal icositetrahedron is the dual of the nonconvex great rhombicuboctahedron. Its faces are darts. Part of each dart lies inside the solid, hence is invisible in solid models.
A pseudo-uniform polyhedron is a polyhedron which has regular polygons as faces and has the same vertex configuration at all vertices but is not vertex-transitive: it is not true that for any two vertices, there exists a symmetry of the polyhedron mapping the first isometrically onto the second. Thus, although all the vertices of a pseudo-uniform polyhedron appear the same, it is not isogonal. They are called pseudo-uniform polyhedra due to their resemblance to some true uniform polyhedra.

In geometry, a planigon is a convex polygon that can fill the plane with only copies of itself. In the Euclidean plane there are 3 regular planigons; equilateral triangle, squares, and regular hexagons; and 8 semiregular planigons; and 4 demiregular planigons which can tile the plane only with other planigons.




































