Pseudo-uniform polyhedron

Last updated September 25, 2022

A pseudo-uniform polyhedron is a polyhedron which has regular polygons as faces and has the same vertex configuration at all vertices but is not vertex-transitive: it is not true that for any two vertices, there exists a symmetry of the polyhedron mapping the first isometrically onto the second. Thus, although all the vertices of a pseudo-uniform polyhedron appear the same, it is not isogonal. They are called pseudo-uniform polyhedra due to their resemblance to some true uniform polyhedra.

The pseudo-uniform polyhedra

Pseudorhombicuboctahedron

The pseudorhombicuboctahedron is the only convex pseudo-uniform polyhedron. It is also a Johnson solid (J₃₇) and can also be called the elongated square gyrobicupola. Its dual is the pseudo-deltoidal icositetrahedron. As the name suggests, it can be constructed by elongating a square gyrobicupola (J₂₉) and inserting an octagonal prism between its two halves. The resulting solid is locally vertex-regular — the arrangement of the four faces incident on any vertex is the same for all vertices; this is unique among the Johnson solids. However, it is not vertex-transitive, and consequently not one of the Archimedean solids, as there are pairs of vertices such that there is no isometry of the solid which maps one into the other. Essentially, the two types of vertices can be distinguished by their "neighbors of neighbors." Another way to see that the polyhedron is not vertex-regular is to note that there is exactly one belt of eight squares around its equator, which distinguishes vertices on the belt from vertices on either side.

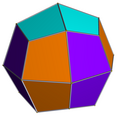
Rhombicuboctahedron	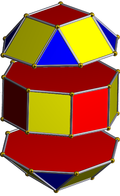Exploded sections	Pseudo-rhombicuboctahedron

The solid can also be seen as the result of twisting one of the square cupolae (J₄) on a rhombicuboctahedron (one of the Archimedean solids; a.k.a. the elongated square orthobicupola) by 45 degrees. Its similarity to the rhombicuboctahedron gives it the alternative name pseudorhombicuboctahedron. It has occasionally been referred to as "the fourteenth Archimedean solid".

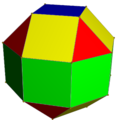
With faces colored by its D_4d symmetry, it can look like this:

pseudorhombicuboctahedron		Pseudo-deltoidal icositetrahedron Dual polyhedron
net

There are 8 (green) squares around its equator, 4 (red) triangles and 4 (yellow) squares above and below, and one (blue) square on each pole.

The construction of the uniform and pseudo rhombicuboctahedra can be seen in the following augmentations of the octagonal prism:

The octagonal prism (coloured with D_8h symmetry)...	...with one of the octagons augmented with a square cupola.	There are two choices on the orientation of the other non-crossed square cupola. One aligns corresponding faces (triangles with triangles, squares with squares) and produces the rhombicuboctahedron. This construction has D_4h symmetry, although the rhombicuboctahedron has full octahedral symmetry.	The other choice aligns noncorresponding faces (triangles with squares) and produces the pseudorhombicuboctahedron. This construction has D_4d symmetry.

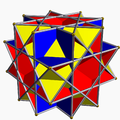
Pseudo-great rhombicuboctahedron

The uniform nonconvex great rhombicuboctahedron may be seen as an octagrammic prism with the octagrams excavated with crossed square cupolae, similarly to how the rhombicuboctahedron may be seen as an octagonal prism with the octagons augmented with square cupolae. Rotating one of the cupolae in this construction results in the pseudo-great rhombicuboctahedron.

Crossed square cupola	Nonconvex great rhombicuboctahedron	Pseudo-great rhombicuboctahedron

The pictures below show the excavation of the octagrammic prism with crossed square cupolae taking place one step at a time. The crossed square cupolae are always red, while the square sides of the octagrammic prism are in the other colours. All images are oriented approximately the same way for clarity.

The octagrammic prism (coloured with D_8h symmetry)...	...with one of the octagrams (here, the top one) excavated with a crossed square cupola. This may be termed the retroelongated crossed square cupola or augmented octagrammic prism, and is isomorphic to the Johnson elongated square cupola.	There are two choices on the orientation of the other crossed square cupola. One aligns corresponding faces (triangles with triangles, squares with squares) and produces the nonconvex great rhombicuboctahedron. This construction has D_4h symmetry, although the nonconvex great rhombicuboctahedron has full octahedral symmetry.	The other choice aligns noncorresponding faces (triangles with squares) and produces the pseudo-great rhombicuboctahedron (or pseudoquasirhombicuboctahedron). This construction has D_4d symmetry.

The pseudo great rhombicuboctahedron has a single "belt" of squares around its equator, and can be constructed by twisting one of the crossed square cupolae on a nonconvex great rhombicuboctahedron by 45 degrees. This is analogous to the pseudorhombicuboctahedron.

Duals of the pseudo-uniform polyhedra

The duals of the pseudo-uniform polyhedra have all faces congruent, but not transitive: their faces do not all lie within the same symmetry orbit and they are thus not isohedral. This is a consequence of the pseudo-uniform polyhedra having the same vertex configuration at every vertex, but not being vertex-transitive. This is demonstrated by the different colours used for the faces in the images of the dual pseudo-uniform polyhedra in this article, denoting different types of faces.

Pseudo-deltoidal icositetrahedron

Pseudo-great deltoidal icositetrahedron

Related Research Articles

In geometry, an Archimedean solid is one of the 13 solids first enumerated by Archimedes. They are the convex uniform polyhedra composed of regular polygons meeting in identical vertices, excluding the five Platonic solids, excluding the prisms and antiprisms, and excluding the pseudorhombicuboctahedron. They are a subset of the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices.

<span class="mw-page-title-main">Cuboctahedron</span> Polyhedron with 8 triangular faces and 6 square faces

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides ; it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform before they refer to it as a “Johnson solid”.

<span class="mw-page-title-main">Rhombicuboctahedron</span> Archimedean solid with 26 faces

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

<span class="mw-page-title-main">Truncated cube</span>

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

<span class="mw-page-title-main">Rhombicosidodecahedron</span> Archimedean solid

In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.

<span class="mw-page-title-main">Truncated cuboctahedron</span> Archimedean solid in geometry

In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

<span class="mw-page-title-main">Truncated icosidodecahedron</span> Archimedean solid

In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.

In geometry, the square cupola, sometimes called lesser dome, is one of the Johnson solids. It can be obtained as a slice of the rhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagon.

In geometry, the elongated square gyrobicupola or pseudo-rhombicuboctahedron is one of the Johnson solids. It is not usually considered to be an Archimedean solid, even though its faces consist of regular polygons that meet in the same pattern at each of its vertices, because unlike the 13 Archimedean solids, it lacks a set of global symmetries that map every vertex to every other vertex. It strongly resembles, but should not be mistaken for, the small rhombicuboctahedron, which is an Archimedean solid. It is also a canonical polyhedron.

In geometry, the square orthobicupola is one of the Johnson solids. As the name suggests, it can be constructed by joining two square cupolae along their octagonal bases, matching like faces. A 45-degree rotation of one cupola before the joining yields a square gyrobicupola.

In geometry, the square gyrobicupola is one of the Johnson solids. Like the square orthobicupola, it can be obtained by joining two square cupolae along their bases. The difference is that in this solid, the two halves are rotated 45 degrees with respect to one another.

In geometry, the triangular orthobicupola is one of the Johnson solids. As the name suggests, it can be constructed by attaching two triangular cupolas along their bases. It has an equal number of squares and triangles at each vertex; however, it is not vertex-transitive. It is also called an anticuboctahedron, twisted cuboctahedron or disheptahedron. It is also a canonical polyhedron.

In geometry, the term semiregular polyhedron is used variously by different authors.

<span class="mw-page-title-main">Uniform polyhedron</span> Isogonal polyhedron with regular faces

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.

In geometry, the great rhombihexahedron (or great rhombicube) is a nonconvex uniform polyhedron, indexed as U₂₁. It has 18 faces (12 squares and 6 octagrams), 48 edges, and 24 vertices. Its dual is the great rhombihexacron. Its vertex figure is a crossed quadrilateral.

<span class="mw-page-title-main">Uniform star polyhedron</span> Self-intersecting uniform polyhedron

In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both.

In geometry, the pseudo great rhombicuboctahedron is one of the two pseudo uniform polyhedra, the other being the convex elongated square gyrobicupola or pseudo rhombicuboctahedron. It has the same vertex figure as the nonconvex great rhombicuboctahedron, but is not a uniform polyhedron, and has a smaller symmetry group. It can be obtained from the great rhombicuboctahedron by taking a square face and the 8 faces with a common vertex to it and rotating them by an angle of π⁄4. It is related to the nonconvex great rhombicuboctahedron in the same way that the pseudo rhombicuboctahedron is related to the rhombicuboctahedron.

<span class="mw-page-title-main">Octadecahedron</span> Polyhedron with 18 faces

In geometry, an octadecahedron is a polyhedron with 18 faces. No octadecahedron is regular; hence, the name does not commonly refer to one specific polyhedron.

In geometry, the crossed square cupola is one of the nonconvex Johnson solid isomorphs, being topologically identical to the convex square cupola. It can be obtained as a slice of the nonconvex great rhombicuboctahedron or quasirhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagram.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.