Omnitruncated polyhedron

In geometry, an omnitruncated polyhedron is a truncated quasiregular polyhedron. When they are alternated, they produce the snub polyhedra.

All omnitruncated polyhedra are considered as zonohedra. They have Wythoff symbol p q r | and vertex figures as 2p.2q.2r.

More generally, an omnitruncated polyhedron is a bevel operator in Conway polyhedron notation.

List of convex omnitruncated polyhedra

There are three convex forms. These forms can be seen as red faces of one regular polyhedron, yellow or green faces of the dual polyhedron, and blue faces at the truncated vertices of the quasiregular polyhedron.

Wythoff symbol p q r |	Omnitruncated polyhedron	Regular/quasiregular polyhedra
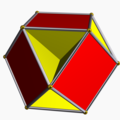
3 3 2 |	Truncated octahedron	Tetrahedron/Octahedron/Tetrahedron
4 3 2 |	Truncated cuboctahedron	Cube/Cuboctahedron/Octahedron
5 3 2 |	Truncated icosidodecahedron	Dodecahedron/Icosidodecahedron/Icosahedron

List of nonconvex omnitruncated polyhedra

There are 5 nonconvex uniform omnitruncated polyhedra.

Wythoff symbol p q r |	Omnitruncated star polyhedron	Wythoff symbol p q r |	Omnitruncated star polyhedron
Right triangle domains (r=2)		General triangle domains
3 4/3 2 |	Great truncated cuboctahedron	4 4/3 3 |	Cubitruncated cuboctahedron
3 5/3 2 |	Great truncated icosidodecahedron	5 5/3 3 |	Icositruncated dodecadodecahedron
5 5/3 2 |	Truncated dodecadodecahedron

Other even-sided nonconvex polyhedra

There are 8 nonconvex forms with mixed Wythoff symbols p q (r s) |, and bow-tie shaped vertex figures, 2p.2q.-2q.-2p. They are not true omnitruncated polyhedra. Instead, the true omnitruncates p q r | or p q s | have coinciding 2r-gonal or 2s-gonal faces that must be removed respectively to form a proper polyhedron. All these polyhedra are one-sided, i.e. non-orientable. The p q r | degenerate Wythoff symbols are listed first, followed by the actual mixed Wythoff symbols.

Omnitruncated polyhedron	Image	Wythoff symbol
Cubohemioctahedron		3/2 2 3 | 2 3 (3/2 3/2) |
Small rhombihexahedron		3/2 2 4 | 2 4 (3/2 4/2) |
Great rhombihexahedron		4/3 3/2 2 | 2 4/3 (3/2 4/2) |
Small rhombidodecahedron		2 5/2 5 | 2 5 (3/2 5/2) |
Small dodecicosahedron		3/2 3 5 | 3 5 (3/2 5/4) |
Rhombicosahedron		2 5/2 3 | 2 3 (5/4 5/2) |
Great dodecicosahedron		5/2 5/3 3 | 3 5/3 (3/2 5/2) |
Great rhombidodecahedron		3/2 5/3 2 | 2 5/3 (3/2 5/4) |

General omnitruncations (bevel)

Omnitruncations are also called cantitruncations or truncated rectifications (tr), and Conway's bevel (b) operator. When applied to nonregular polyhedra, new polyhedra can be generated, for example these 2-uniform polyhedra:

Coxeter	trrC	trrD	trtT	trtC	trtO	trtI
Conway	baO	baD	btT	btC	btO	btI
Image

See also

• Uniform polyhedron

References

• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916): 401–450, Bibcode:1954RSPTA.246..401C, doi:10.1098/rsta.1954.0003, ISSN   0080-4614, JSTOR   91532, MR   0062446, S2CID   202575183
• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN   0-521-09859-9.
• Skilling, J. (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 278 (1278): 111–135, Bibcode:1975RSPTA.278..111S, doi:10.1098/rsta.1975.0022, ISSN   0080-4614, JSTOR   74475, MR   0365333, S2CID   122634260
• Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har'El, Kaleido software, Images, dual images
• Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993.

Polyhedron operators

• v
• t
• e

Seed	Truncation	Rectification	Bitruncation	Dual	Expansion	Omnitruncation	Alternations
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q} s{q,p}	ht012{p,q} sr{p,q}