Disphenoid

Last updated • 4 min readFrom Wikipedia, The Free Encyclopedia

Disphenoid tetrahedron.png
The tetragonal and digonal disphenoids can be positioned inside a cuboid bisecting two opposite faces. Both have four equal edges going around the sides. The digonal has two pairs of congruent isosceles triangle faces, while the tetragonal has four congruent isosceles triangle faces.
Rhombic disphenoid.png
A rhombic disphenoid has congruent scalene triangle faces, and can fit diagonally inside of a cuboid. It has three sets of edge lengths, existing as opposite pairs.

In geometry, a disphenoid (from Greek sphenoeides 'wedgelike') is a tetrahedron whose four faces are congruent acute-angled triangles. [1] It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron, [2] sphenoid, [3] bisphenoid, [3] isosceles tetrahedron, [4] equifacial tetrahedron, [5] almost regular tetrahedron, [6] and tetramonohedron. [7]

Contents

All the solid angles and vertex figures of a disphenoid are the same, and the sum of the face angles at each vertex is equal to two right angles. However, a disphenoid is not a regular polyhedron, because, in general, its faces are not regular polygons, and its edges have three different lengths.

Special cases and generalizations

If the faces of a disphenoid are equilateral triangles, it is a regular tetrahedron with Td tetrahedral symmetry, although this is not normally called a disphenoid. When the faces of a disphenoid are isosceles triangles, it is called a tetragonal disphenoid. In this case it has D2d dihedral symmetry. A sphenoid with scalene triangles as its faces is called a rhombic disphenoid and it has D2 dihedral symmetry. Unlike the tetragonal disphenoid, the rhombic disphenoid has no reflection symmetry, so it is chiral. [8] Both tetragonal disphenoids and rhombic disphenoids are isohedra: as well as being congruent to each other, all of their faces are symmetric to each other.

It is not possible to construct a disphenoid with right triangle or obtuse triangle faces. [4] When right triangles are glued together in the pattern of a disphenoid, they form a flat figure (a doubly-covered rectangle) that does not enclose any volume. [8] When obtuse triangles are glued in this way, the resulting surface can be folded to form a disphenoid (by Alexandrov's uniqueness theorem) but one with acute triangle faces and with edges that in general do not lie along the edges of the given obtuse triangles.

Two more types of tetrahedron generalize the disphenoid and have similar names. The digonal disphenoid has faces with two different shapes, both isosceles triangles, with two faces of each shape. The phyllic disphenoid similarly has faces with two shapes of scalene triangles.

Disphenoids can also be seen as digonal antiprisms or as alternated quadrilateral prisms.

Characterizations

A tetrahedron is a disphenoid if and only if its circumscribed parallelepiped is right-angled. [9]

We also have that a tetrahedron is a disphenoid if and only if the center in the circumscribed sphere and the inscribed sphere coincide. [10]

Another characterization states that if d1, d2 and d3 are the common perpendiculars of AB and CD; AC and BD; and AD and BC respectively in a tetrahedron ABCD, then the tetrahedron is a disphenoid if and only if d1, d2 and d3 are pairwise perpendicular. [9]

The disphenoids are the only polyhedra having infinitely many non-self-intersecting closed geodesics. On a disphenoid, all closed geodesics are non-self-intersecting. [11]

The disphenoids are the tetrahedra in which all four faces have the same perimeter, the tetrahedra in which all four faces have the same area, [10] and the tetrahedra in which the angular defects of all four vertices equal π. They are the polyhedra having a net in the shape of an acute triangle, divided into four similar triangles by segments connecting the edge midpoints. [6]

Metric formulas

The volume of a disphenoid with opposite edges of length l, m and n is given by: [12]

The circumscribed sphere has radius [12] (the circumradius):

and the inscribed sphere has radius: [12]

where V is the volume of the disphenoid and T is the area of any face, which is given by Heron's formula. There is also the following interesting relation connecting the volume and the circumradius: [12]

The squares of the lengths of the bimedians are: [12]

Other properties

If the four faces of a tetrahedron have the same perimeter, then the tetrahedron is a disphenoid. [10]

If the four faces of a tetrahedron have the same area, then it is a disphenoid. [9] [10]

The centers in the circumscribed and inscribed spheres coincide with the centroid of the disphenoid. [12]

The bimedians are perpendicular to the edges they connect and to each other. [12]

Honeycombs and crystals

A space-filling tetrahedral disphenoid inside a cube. Two edges have dihedral angles of 90deg, and four edges have dihedral angles of 60deg. Oblate tetrahedrille cell.png
A space-filling tetrahedral disphenoid inside a cube. Two edges have dihedral angles of 90°, and four edges have dihedral angles of 60°.

Some tetragonal disphenoids will form honeycombs. The disphenoid whose four vertices are (-1, 0, 0), (1, 0, 0), (0, 1, 1), and (0, 1, -1) is such a disphenoid. [13] [14] Each of its four faces is an isosceles triangle with edges of lengths √3, √3, and 2. It can tessellate space to form the disphenoid tetrahedral honeycomb. As Gibb (1990) describes, it can be folded without cutting or overlaps from a single sheet of a4 paper. [15]

"Disphenoid" is also used to describe two forms of crystal:

Other uses

Six tetragonal disphenoids attached end-to-end in a ring construct a kaleidocycle, a paper toy that can rotate on 4 sets of faces in a hexagon. The rotation of the six disphenoids with opposite edges of length l, m and n (without loss of generality n≤l, n≤m) is physically realizable if and only if [16]

See also

Related Research Articles

In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar and a bipyramid is usually symmetric, meaning the two pyramids are mirror images across their common base plane. When each apex of the bipyramid is on a line perpendicular to the base and passing through its center, it is a right bipyramid; otherwise it is oblique. When the base is a regular polygon, the bipyramid is also called regular.

<span class="mw-page-title-main">Cuboctahedron</span> Polyhedron with 8 triangular faces and 6 square faces

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral. Its dual polyhedron is the rhombic dodecahedron.

In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, an octahedron is a polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. Many types of irregular octahedra also exist, including both convex and non-convex shapes.

In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:

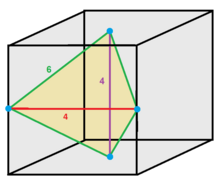
In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra.

<span class="mw-page-title-main">Kite (geometry)</span> Quadrilateral symmetric across a diagonal

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

<span class="mw-page-title-main">Truncated tetrahedron</span> Archimedean solid with 8 faces

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges. It can be constructed by truncating all 4 vertices of a regular tetrahedron.

<span class="mw-page-title-main">Trapezohedron</span> Polyhedron made of congruent kites arranged radially

In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron, is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.

<span class="mw-page-title-main">Tetrakis hexahedron</span> Catalan solid with 24 faces

In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.

<span class="mw-page-title-main">Snub disphenoid</span> Convex polyhedron with 12 triangular faces

In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape is also called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron.

<span class="mw-page-title-main">Cubic honeycomb</span> Only regular space-filling tessellation of the cube

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

<span class="mw-page-title-main">Bitruncated cubic honeycomb</span>

The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra. It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.

<span class="mw-page-title-main">Tetragonal disphenoid honeycomb</span>

The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John Horton Conway calls it an oblate tetrahedrille or shortened to obtetrahedrille.

<span class="mw-page-title-main">Truncated 5-cell</span>

In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.

<span class="mw-page-title-main">Midsphere</span> Sphere tangent to every edge of a polyhedron

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.

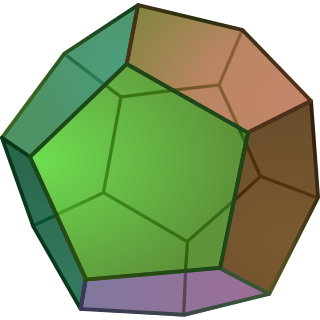
<span class="mw-page-title-main">Regular dodecahedron</span> Convex polyhedron with 12 regular pentagonal faces

A regular dodecahedron or pentagonal dodecahedron is a dodecahedron composed of regular pentagonal faces, three meeting at each vertex. It is an example of Platonic solids, described as cosmic stellation by Plato in his dialogues, and it was used as part of Solar System proposed by Johannes Kepler. However, the regular dodecahedron, including the other Platonic solids, has already been described by other philosophers since antiquity.

<span class="mw-page-title-main">Compound of two tetrahedra</span> Polyhedral compound

In geometry, a compound of two tetrahedra is constructed by two overlapping tetrahedra, usually implied as regular tetrahedra.

<span class="mw-page-title-main">Ten-of-diamonds decahedron</span>

In geometry, the ten-of-diamonds decahedron is a space-filling polyhedron with 10 faces, 2 opposite rhombi with orthogonal major axes, connected by 8 identical isosceles triangle faces. Although it is convex, it is not a Johnson solid because its faces are not composed entirely of regular polygons. Michael Goldberg named it after a playing card, as a 10-faced polyhedron with two opposite rhombic (diamond-shaped) faces. He catalogued it in a 1982 paper as 10-II, the second in a list of 26 known space-filling decahedra.

<span class="mw-page-title-main">Ideal polyhedron</span> Shape in hyperbolic geometry

In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.

References

  1. ↑ Coxeter, H. S. M. (1973), Regular Polytopes (3rd ed.), Dover Publications, p.  15, ISBN   0-486-61480-8
  2. ↑ Akiyama, Jin; Matsunaga, Kiyoko (2020), "An Algorithm for Folding a Conway Tile into an Isotetrahedron or a Rectangle Dihedron", Journal of Information Processing , 28 (28): 750–758, doi: 10.2197/ipsjjip.28.750 , S2CID   230108666 .
  3. 1 2 Whittaker, E. J. W. (2013), Crystallography: An Introduction for Earth Science (and other Solid State) Students, Elsevier, p. 89, ISBN   9781483285566 .
  4. 1 2 Leech, John (1950), "Some properties of the isosceles tetrahedron", The Mathematical Gazette , 34 (310): 269–271, doi:10.2307/3611029, JSTOR   3611029, MR   0038667, S2CID   125145099 .
  5. ↑ Hajja, Mowaffaq; Walker, Peter (2001), "Equifacial tetrahedra", International Journal of Mathematical Education in Science and Technology, 32 (4): 501–508, doi:10.1080/00207390110038231, MR   1847966, S2CID   218495301 .
  6. 1 2 Akiyama, Jin (2007), "Tile-makers and semi-tile-makers", American Mathematical Monthly , 114 (7): 602–609, doi:10.1080/00029890.2007.11920450, JSTOR   27642275, MR   2341323, S2CID   32897155 .
  7. ↑ Demaine, Erik; O'Rourke, Joseph (2007), Geometric Folding Algorithms, Cambridge University Press, p. 424, ISBN   978-0-521-71522-5 .
  8. 1 2 Petitjean, Michel (2015), "The most chiral disphenoid" (PDF), MATCH Communications in Mathematical and in Computer Chemistry, 73 (2): 375–384, MR   3242747 .
  9. 1 2 3 Andreescu, Titu; Gelca, Razvan (2009), Mathematical Olympiad Challenges (2nd ed.), Birkhäuser, pp. 30–31.
  10. 1 2 3 4 Brown, B. H. (April 1926), "Theorem of Bang. Isosceles tetrahedra", Undergraduate Mathematics Clubs: Club Topics, American Mathematical Monthly , 33 (4): 224–226, doi:10.1080/00029890.1926.11986564, JSTOR   2299548 .
  11. ↑ Fuchs, Dmitry [in German]; Fuchs, Ekaterina (2007), "Closed geodesics on regular polyhedra" (PDF), Moscow Mathematical Journal, 7 (2): 265–279, 350, doi:10.17323/1609-4514-2007-7-2-265-279, MR   2337883 .
  12. 1 2 3 4 5 6 7 Leech, John (1950), "Some properties of the isosceles tetrahedron", Mathematical Gazette, 34 (310): 269–271, doi:10.2307/3611029, JSTOR   3611029, S2CID   125145099 .
  13. ↑ Coxeter (1973 , pp. 71–72).
  14. ↑ Senechal, Marjorie (1981), "Which tetrahedra fill space?", Mathematics Magazine , 54 (5): 227–243, doi:10.2307/2689983, JSTOR   2689983, MR   0644075
  15. ↑ Gibb, William (1990), "Paper patterns: solid shapes from metric paper", Mathematics in School, 19 (3): 2–4 Reprinted in Pritchard, Chris, ed. (2003), The Changing Shape of Geometry: Celebrating a Century of Geometry and Geometry Teaching, Cambridge University Press, pp. 363–366, ISBN   0-521-53162-4
  16. ↑ Sloane, N. J. A. (ed.), "SequenceA338336", The On-Line Encyclopedia of Integer Sequences , OEIS Foundation{{cite web}}: CS1 maint: overridden setting (link)
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.