Edge (geometry)

Last updated

In geometry, an edge is a particular type of line segment joining two vertices in a polygon, polyhedron, or higher-dimensional polytope. [1] In a polygon, an edge is a line segment on the boundary, [2] and is often called a polygon side. In a polyhedron or more generally a polytope, an edge is a line segment where two faces (or polyhedron sides) meet. [3] A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal.

Contents

An edge may also be an infinite line separating two half-planes. [4] The sides of a plane angle are semi-infinite half-lines (or rays). [5]

Relation to edges in graphs

In graph theory, an edge is an abstract object connecting two graph vertices, unlike polygon and polyhedron edges which have a concrete geometric representation as a line segment. However, any polyhedron can be represented by its skeleton or edge-skeleton, a graph whose vertices are the geometric vertices of the polyhedron and whose edges correspond to the geometric edges. [6] Conversely, the graphs that are skeletons of three-dimensional polyhedra can be characterized by Steinitz's theorem as being exactly the 3-vertex-connected planar graphs. [7]

Number of edges in a polyhedron

Any convex polyhedron's surface has Euler characteristic

where V is the number of vertices, E is the number of edges, and F is the number of faces. This equation is known as Euler's polyhedron formula. Thus the number of edges is 2 less than the sum of the numbers of vertices and faces. For example, a cube has 8 vertices and 6 faces, and hence 12 edges.

Incidences with other faces

In a polygon, two edges meet at each vertex; more generally, by Balinski's theorem, at least d edges meet at every vertex of a d-dimensional convex polytope. [8] Similarly, in a polyhedron, exactly two two-dimensional faces meet at every edge, [9] while in higher dimensional polytopes three or more two-dimensional faces meet at every edge.

Alternative terminology

In the theory of high-dimensional convex polytopes, a facet or side of a d-dimensional polytope is one of its (d − 1)-dimensional features, a ridge is a (d − 2)-dimensional feature, and a peak is a (d − 3)-dimensional feature. Thus, the edges of a polygon are its facets, the edges of a 3-dimensional convex polyhedron are its ridges, and the edges of a 4-dimensional polytope are its peaks. [10]

See also

Related Research Articles

<span class="mw-page-title-main">Cuboctahedron</span> Polyhedron with 8 triangular faces and 6 square faces

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral. Its dual polyhedron is the rhombic dodecahedron.

<span class="mw-page-title-main">Cube</span> Solid object with six equal square faces

In geometry, a cube is a three-dimensional solid object bounded by six square faces. It has twelve edges and eight vertices. It can be represented as a rectangular cuboid with six square faces, or a parallelepiped with equal edges. It is an example of many type of solids: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.

<span class="mw-page-title-main">Dual polyhedron</span> Polyhedron associated with another by swapping vertices for faces

In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

<span class="mw-page-title-main">Icosidodecahedron</span> Archimedean solid with 32 faces

In geometry, an icosidodecahedron or pentagonal gyrobirotunda is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such, it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

<span class="mw-page-title-main">Polyhedron</span> 3D shape with flat faces, straight edges and sharp corners

In geometry, a polyhedron is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices.

<span class="mw-page-title-main">4-polytope</span> Four-dimensional geometric object with flat sides

In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.

<span class="mw-page-title-main">Truncated icosahedron</span> A polyhedron resembling a soccerball

In geometry, the truncated icosahedron is a polyhedron that can be constructed by truncating all of the regular icosahedron's vertices. Intuitively, it may be regarded as footballs that are typically patterned with white hexagons and black pentagons. It can be found in the application of geodesic dome structures such as those whose architecture Buckminster Fuller pioneered are often based on this structure. It is an example of an Archimedean solid, as well as a Goldberg polyhedron.

In solid geometry, a face is a flat surface that forms part of the boundary of a solid object; a three-dimensional solid bounded exclusively by faces is a polyhedron. A face can be finite like a polygon or circle, or infinite like a half-plane or plane.

<span class="mw-page-title-main">Truncated tetrahedron</span> Archimedean solid with 8 faces

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges. It can be constructed by truncating all 4 vertices of a regular tetrahedron.

In geometry, a polytope or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces.

<span class="mw-page-title-main">Net (polyhedron)</span> Edge-joined polygons which fold into a polyhedron

In geometry, a net of a polyhedron is an arrangement of non-overlapping edge-joined polygons in the plane which can be folded to become the faces of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and solid geometry in general, as they allow for physical models of polyhedra to be constructed from material such as thin cardboard.

<span class="mw-page-title-main">Convex polytope</span> Convex hull of a finite set of points in a Euclidean space

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

<span class="mw-page-title-main">Rectification (geometry)</span> Operation in Euclidean geometry

In Euclidean geometry, rectification, also known as critical truncation or complete-truncation, is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope.

<span class="mw-page-title-main">Geometric graph theory</span> Subfield of graph theory

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices; thus, it can be described as "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.

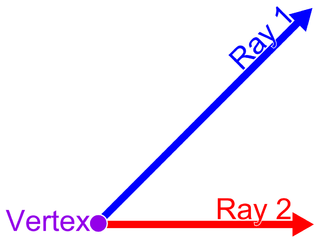
<span class="mw-page-title-main">Vertex (geometry)</span> Point where two or more curves, lines, or edges meet

In geometry, a vertex is a point where two or more curves, lines, or edges meet or intersect. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedron are vertices.

Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

<span class="mw-page-title-main">Polyhedral graph</span> Graph made from vertices and edges of a convex polyhedron

In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected, planar graphs.

<span class="mw-page-title-main">Balinski's theorem</span> Graphs of d-dimensional polytopes are d-connected

In polyhedral combinatorics, a branch of mathematics, Balinski's theorem is a statement about the graph-theoretic structure of three-dimensional convex polyhedra and higher-dimensional convex polytopes. It states that, if one forms an undirected graph from the vertices and edges of a convex d-dimensional convex polyhedron or polytope, then the resulting graph is at least d-vertex-connected: the removal of any d − 1 vertices leaves a connected subgraph. For instance, for a three-dimensional polyhedron, even if two of its vertices are removed, for any pair of vertices there will still exist a path of vertices and edges connecting the pair.

<span class="mw-page-title-main">Toroidal polyhedron</span> Partition of a toroidal surface into polygons

In geometry, a toroidal polyhedron is a polyhedron which is also a toroid, having a topological genus of 1 or greater. Notable examples include the Császár and Szilassi polyhedra.

References

  1. ↑ Ziegler, Günter M. (1995), Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152, Springer, Definition 2.1, p. 51, ISBN   9780387943657 .
  2. ↑ Weisstein, Eric W. "Polygon Edge". From Wolfram MathWorld.
  3. ↑ Weisstein, Eric W. "Polytope Edge". From Wolfram MathWorld.
  4. ↑ Wylie Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill, p. 64, ISBN   0-07-072191-2
  5. ↑ Wylie Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill, p. 68, ISBN   0-07-072191-2
  6. ↑ Senechal, Marjorie (2013), Shaping Space: Exploring Polyhedra in Nature, Art, and the Geometrical Imagination, Springer, p. 81, ISBN   9780387927145 .
  7. ↑ Pisanski, Tomaž; Randić, Milan (2000), "Bridges between geometry and graph theory", in Gorini, Catherine A. (ed.), Geometry at work, MAA Notes, vol. 53, Washington, DC: Math. Assoc. America, pp. 174–194, MR   1782654 . See in particular Theorem 3, p. 176.
  8. ↑ Balinski, M. L. (1961), "On the graph structure of convex polyhedra in n-space", Pacific Journal of Mathematics, 11 (2): 431–434, doi: 10.2140/pjm.1961.11.431 , MR   0126765 .
  9. ↑ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 1, ISBN   9780521098595 .
  10. ↑ Seidel, Raimund (1986), "Constructing higher-dimensional convex hulls at logarithmic cost per face", Proceedings of the Eighteenth Annual ACM Symposium on Theory of Computing (STOC '86), pp. 404–413, doi:10.1145/12130.12172, S2CID   8342016 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.