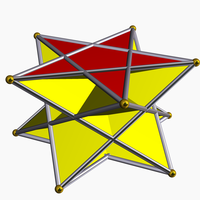
In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter–Dynkin diagram of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces, intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex.
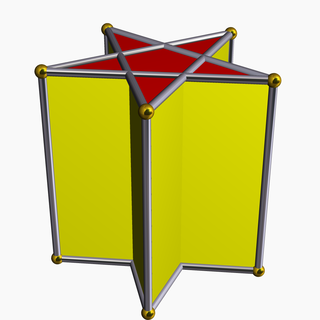
In geometry, the pentagrammic prism is one of an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.

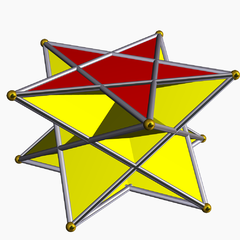
In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5⁄2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.

In geometry, the great stellated dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol {5⁄2,3}. It is one of four nonconvex regular polyhedra.

In geometry, the great icosahedron is one of four Kepler-Poinsot polyhedra, with Schläfli symbol {3,5⁄2} and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.
A snub polyhedron is a polyhedron obtained by alternating a corresponding omnitruncated or truncated polyhedron, depending on the definition. Some but not all authors include antiprisms as snub polyhedra, as they are obtained by this construction from a degenerate "polyhedron" with only two faces.

In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.

In geometry, the small ditrigonal icosidodecahedron (or small ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U30. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol a{5,3}, as an altered dodecahedron, and Coxeter diagram or .
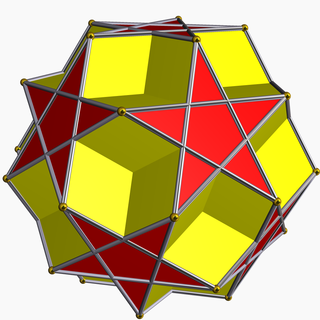
In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U36. It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

In geometry, the great icosidodecahedron is a nonconvex uniform polyhedron, indexed as U54. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 30 vertices. It is given a Schläfli symbol r{3,5⁄2}. It is the rectification of the great stellated dodecahedron and the great icosahedron. It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

In geometry, the ditrigonal dodecadodecahedron (or ditrigonary dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U41. It has 24 faces (12 pentagons and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol b{5,5⁄2}, as a blended great dodecahedron, and Coxeter diagram . It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 | 5⁄3 5, and Coxeter diagram .
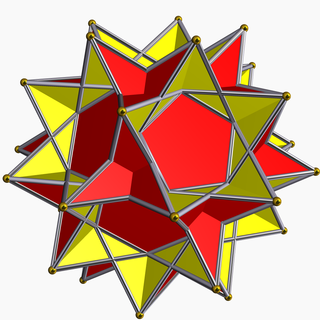
In geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. It has 18 faces (12 pentagrams and 6 decagrams), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the small dodecahemicosahedron (or great dodecahemiicosahedron) is a nonconvex uniform polyhedron, indexed as U62. It has 22 faces (12 pentagrams and 10 hexagons), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great snub dodecicosidodecahedron (or great snub dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U64. It has 104 faces (80 triangles and 24 pentagrams), 180 edges, and 60 vertices. It has Coxeter diagram, . It has the unusual feature that its 24 pentagram faces occur in 12 coplanar pairs.
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.

This uniform polyhedron compound is a symmetric arrangement of 6 pentagrammic crossed antiprisms. It can be constructed by inscribing within a great icosahedron one pentagrammic crossed antiprism in each of the six possible ways, and then rotating each by 36 degrees about its axis. It shares its vertices with the compound of 6 pentagonal antiprisms.

This uniform polyhedron compound is a symmetric arrangement of 12 pentagrammic crossed antiprisms. It can be constructed by inscribing one pair of pentagrammic crossed antiprisms within a great icosahedron, in each of the six possible ways, and then rotating each by an equal and opposite angle θ.