
In geometry, a Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, called coordinate lines, coordinate axes or just axes of the system. The point where they meet is called the origin and has (0, 0) as coordinates.

Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which are called Euclidean n-spaces when one wants to specify their dimension. For n equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

In Euclidean geometry, an affine transformation or affinity is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.
In geometry, an improper rotation is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicular to that axis. Reflection and inversion are each a special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation. It is used as a symmetry operation in the context of geometric symmetry, molecular symmetry and crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have improper rotation symmetry.

In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as a set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection. For example the mirror image of the small Latin letter p for a reflection with respect to a vertical axis would look like q. Its image by reflection in a horizontal axis would look like b. A reflection is an involution: when applied twice in succession, every point returns to its original location, and every geometrical object is restored to its original state.
In mathematics, the affine group or general affine group of any affine space is the group of all invertible affine transformations from the space into itself. In the case of a Euclidean space, the affine group consists of those functions from the space to itself such that the image of every line is a line.

A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. For each wallpaper there corresponds a group of congruent transformations, with function composition as the group operation. Thus, a wallpaper group is a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations, tiles and physical wallpaper.

Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have a sign (as in the sign of an angle): a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space.

In geometry, a glide reflection or transflection is a geometric transformation that consists of a reflection across a hyperplane and a translation ("glide") in a direction parallel to that hyperplane, combined into a single transformation. Because the distances between points are not changed under glide reflection, it is a motion or isometry. When the context is the two-dimensional Euclidean plane, the hyperplane of reflection is a straight line called the glide line or glide axis. When the context is three-dimensional space, the hyperplane of reflection is a plane called the glide plane. The displacement vector of the translation is called the glide vector.
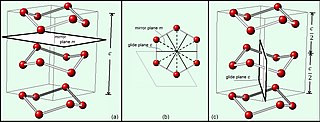
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups.

Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.
In geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length. There are four types: translations, rotations, reflections, and glide reflections.
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.
In a group, the conjugate by g of h is ghg−1.

In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of n-dimensional hyperbolic geometry in which points are represented by points on the forward sheet S+ of a two-sheeted hyperboloid in (n+1)-dimensional Minkowski space or by the displacement vectors from the origin to those points, and m-planes are represented by the intersections of (m+1)-planes passing through the origin in Minkowski space with S+ or by wedge products of m vectors. Hyperbolic space is embedded isometrically in Minkowski space; that is, the hyperbolic distance function is inherited from Minkowski space, analogous to the way spherical distance is inherited from Euclidean distance when the n-sphere is embedded in (n+1)-dimensional Euclidean space.

In geometry, a point reflection is a transformation of affine space in which every point is reflected across a specific fixed point. When dealing with crystal structures and in the physical sciences the terms inversion symmetry, inversion center or centrosymmetric are more commonly used.
The Banach–Tarski paradox is a theorem in set-theoretic geometry, which states the following: Given a solid ball in three-dimensional space, there exists a decomposition of the ball into a finite number of disjoint subsets, which can then be put back together in a different way to yield two identical copies of the original ball. Indeed, the reassembly process involves only moving the pieces around and rotating them without changing their shape. However, the pieces themselves are not "solids" in the usual sense, but infinite scatterings of points. The reconstruction can work with as few as five pieces.

In geometry, an object has symmetry if there is an operation or transformation that maps the figure/object onto itself. Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be symmetric under rotation or to have rotational symmetry. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry.




























