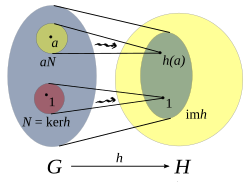
Group homomorphisms
Let  be the cyclic group on 6 elements
be the cyclic group on 6 elements  with modular addition,
with modular addition,  be the cyclic on 2 elements
be the cyclic on 2 elements  with modular addition, and
with modular addition, and  the homomorphism that maps each element
the homomorphism that maps each element  to the element
to the element  modulo 2 in
modulo 2 in  . Then
. Then  , since all these elements are mapped to
, since all these elements are mapped to  . The quotient group
. The quotient group  has two elements:
has two elements:  and
and  , and is isomorphic to
, and is isomorphic to  . [22]
. [22]
Given a isomorphism  , one has
, one has  . [22] On the other hand, if this mapping is merely a homomorphism where H is the trivial group, then
. [22] On the other hand, if this mapping is merely a homomorphism where H is the trivial group, then  for all
for all  , so thus
, so thus  . [22]
. [22]
Let  be the map defined as
be the map defined as  . Then this is a homomorphism with the kernel consisting precisely the points of the form
. Then this is a homomorphism with the kernel consisting precisely the points of the form  . This mapping is considered the "projection onto the x-axis." [22] A similar phenomenon occurs with the mapping
. This mapping is considered the "projection onto the x-axis." [22] A similar phenomenon occurs with the mapping  defined as
defined as  , where the kernel is the points of the form
, where the kernel is the points of the form  [9]
[9]
For a non-abelian example, let  denote the Quaternion group, and
denote the Quaternion group, and  the Klein 4-group. Define a mapping
the Klein 4-group. Define a mapping  to be: [22]
to be: [22]




Then this mapping is a homomorphism where  . [22]
. [22]
Let  denote the circle group, consisting of all complex numbers with absolute value (or modulus) of
denote the circle group, consisting of all complex numbers with absolute value (or modulus) of  , with the group operation being multiplication. [23] Then the function
, with the group operation being multiplication. [23] Then the function  sending
sending  is a homomorphism with the integers being the kernel. The first isomorphism theorem then implies that
is a homomorphism with the integers being the kernel. The first isomorphism theorem then implies that  . [24]
. [24]
The symmetric group on  elements,
elements,  , has a surjective homomorphism
, has a surjective homomorphism  that takes each permutation to the parity of the number of transpositions whose product is that permutation. The alternating group
that takes each permutation to the parity of the number of transpositions whose product is that permutation. The alternating group  is the kernel of this homomorphism, consisting of the even permutations. The alternating group is a non-abelian simple group for
is the kernel of this homomorphism, consisting of the even permutations. The alternating group is a non-abelian simple group for  . [25]
. [25]
The determinant of  invertible matrices of the real numbers
invertible matrices of the real numbers  , whose set is denoted
, whose set is denoted  and called the general linear group of
and called the general linear group of  matrices of
matrices of  , is a homomorphism onto the multiplication group
, is a homomorphism onto the multiplication group  (consisting of all non-zero real numbers), and the kernel of the determinant is called the special linear group
(consisting of all non-zero real numbers), and the kernel of the determinant is called the special linear group  of
of  matrices of
matrices of  . These are the matrices whose determinant is precisely
. These are the matrices whose determinant is precisely  . [26]
. [26]
Given a group  and an element, the mapping
and an element, the mapping  is an automorphism - an isomorphism whose domain and image are the same group. This gives a homomorphism from
is an automorphism - an isomorphism whose domain and image are the same group. This gives a homomorphism from  to its automorphism group
to its automorphism group  , mapping each
, mapping each  to its respective inner automorphism as described, and the kernel of this homomorphism is the center
to its respective inner automorphism as described, and the kernel of this homomorphism is the center  of
of  , consisting of
, consisting of  where for every
where for every  , we have
, we have  , or equivalently
, or equivalently  . More generally, for every normal subgroup
. More generally, for every normal subgroup  of
of  (i.e. groups closed under conjugation), this conjugation map is also an automorphism on
(i.e. groups closed under conjugation), this conjugation map is also an automorphism on  , giving another homomorphism
, giving another homomorphism  to
to  , with the kernel being the centralizer
, with the kernel being the centralizer  of
of  in
in  , being the set of
, being the set of  where for every
where for every  , we have
, we have  . [27]
. [27]
Linear maps
Let  be defined as
be defined as  , then the kernel of
, then the kernel of  (that is, the null space) will be the set of points
(that is, the null space) will be the set of points  such that
such that  , and this set is a subspace of
, and this set is a subspace of  (the same is true for every kernel of a linear map). [17]
(the same is true for every kernel of a linear map). [17]
If  represents the derivative operator on real polynomials, then the kernel of
represents the derivative operator on real polynomials, then the kernel of  will consist of the polynomials with deterivative equal to 0, that is the constant functions. [17]
will consist of the polynomials with deterivative equal to 0, that is the constant functions. [17]
Consider the mapping  , where
, where  is a polynomial with real coefficients. Then
is a polynomial with real coefficients. Then  is a linear map whose kernel is precisely 0, since 0 is the only polynomial to satisfy
is a linear map whose kernel is precisely 0, since 0 is the only polynomial to satisfy  for all
for all  . [17]
. [17]
![An example for a kernel - the linear operator
L
:
(
x
,
y
)
[?]
(
x
,
x
)
{\displaystyle L:(x,y)\longrightarrow (x,x)}
transforms all points on the
(
x
=
0
,
y
)
{\displaystyle (x=0,y)}
line to the zero point
(
0
,
0
)
{\displaystyle (0,0)}
, thus they form the kernel for the linear operator Projection-on-diagonal.gif](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e3/Projection-on-diagonal.gif/330px-Projection-on-diagonal.gif)




















































































































































































































































































