Rotational symmetry

Last updated April 06, 2024

Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.

Formal treatment

Formally the rotational symmetry is symmetry with respect to some or all rotations in $m$ -dimensional Euclidean space. Rotations are direct isometries, i.e., isometries preserving orientation. Therefore, a symmetry group of rotational symmetry is a subgroup of $E + (m)$ (see Euclidean group).

Symmetry with respect to all rotations about all points implies translational symmetry with respect to all translations, so space is homogeneous, and the symmetry group is the whole $E (m)$ . With the modified notion of symmetry for vector fields the symmetry group can also be $E + (m)$ .

For symmetry with respect to rotations about a point we can take that point as origin. These rotations form the special orthogonal group $SO(m)$ , the group of $m \times m$ orthogonal matrices with determinant 1. For $m = 3$ this is the rotation group $SO(3)$ .

In another definition of the word, the rotation group of an object is the symmetry group within $E + (n)$ , the group of direct isometries; in other words, the intersection of the full symmetry group and the group of direct isometries. For chiral objects it is the same as the full symmetry group.

Laws of physics are SO(3)-invariant if they do not distinguish different directions in space. Because of Noether's theorem, the rotational symmetry of a physical system is equivalent to the angular momentum conservation law.

Discrete rotational symmetry

Rotational symmetry of order $n$ , also called $n$ -fold rotational symmetry, or discrete rotational symmetry of the $n$ th order, with respect to a particular point (in 2D) or axis (in 3D) means that rotation by an angle of ${\tfrac {360^{\circ }}{n}}$ (180°, 120°, 90°, 72°, 60°, 51 3⁄7°, etc.) does not change the object. A "1-fold" symmetry is no symmetry (all objects look alike after a rotation of 360°).

The notation for $n$ -fold symmetry is $C n$ or simply $n$ . The actual symmetry group is specified by the point or axis of symmetry, together with the $n$ . For each point or axis of symmetry, the abstract group type is cyclic group of order $n$ , $Z n$ . Although for the latter also the notation $C n$ is used, the geometric and abstract $C n$ should be distinguished: there are other symmetry groups of the same abstract group type which are geometrically different, see cyclic symmetry groups in 3D.

The fundamental domain is a sector of ${\tfrac {360^{\circ }}{n}}.$

Examples without additional reflection symmetry:

$n = 2$ , 180°: the dyad; letters Z, N, S; the outlines, albeit not the colors, of the yin and yang symbol; the Union Flag (as divided along the flag's diagonal and rotated about the flag's center point)
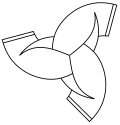
$n = 3$ , 120°: triad, triskelion, Borromean rings; sometimes the term trilateral symmetry is used;
$n = 4$ , 90°: tetrad, swastika
$n = 6$ , 60°: hexad, Star of David (this one has additional reflection symmetry)
$n = 8$ , 45°: octad, Octagonal muqarnas, computer-generated (CG), ceiling

$C n$ is the rotation group of a regular $n$ -sided polygon in 2D and of a regular $n$ -sided pyramid in 3D.

If there is e.g. rotational symmetry with respect to an angle of 100°, then also with respect to one of 20°, the greatest common divisor of 100° and 360°.

A typical 3D object with rotational symmetry (possibly also with perpendicular axes) but no mirror symmetry is a propeller.

Examples

$C 2$ (more)	$C 3$ (more)	$C 4$ (more)	$C 5$ (more)	$C 6$ (more)
Double Pendulum fractal	Roundabout traffic sign		US Bicentennial Star
The starting position in shogi	Snoldelev Stone's interlocked drinking horns design

Multiple symmetry axes through the same point

For discrete symmetry with multiple symmetry axes through the same point, there are the following possibilities:

In addition to an $n$ -fold axis, $n$ perpendicular 2-fold axes: the dihedral groups $D n$ of order $2 n$ ( $n \geq 2$ ). This is the rotation group of a regular prism, or regular bipyramid. Although the same notation is used, the geometric and abstract $D n$ should be distinguished: there are other symmetry groups of the same abstract group type which are geometrically different, see dihedral symmetry groups in 3D.
4×3-fold and 3×2-fold axes: the rotation group $T$ of order 12 of a regular tetrahedron. The group is isomorphic to alternating group $A 4$ .
3×4-fold, 4×3-fold, and 6×2-fold axes: the rotation group O of order 24 of a cube and a regular octahedron. The group is isomorphic to symmetric group $S 4$ .
6×5-fold, 10×3-fold, and 15×2-fold axes: the rotation group $I$ of order 60 of a dodecahedron and an icosahedron. The group is isomorphic to alternating group $A 5$ . The group contains 10 versions of $D 3$ and 6 versions of $D 5$ (rotational symmetries like prisms and antiprisms).

In the case of the Platonic solids, the 2-fold axes are through the midpoints of opposite edges, and the number of them is half the number of edges. The other axes are through opposite vertices and through centers of opposite faces, except in the case of the tetrahedron, where the 3-fold axes are each through one vertex and the center of one face.

Rotational symmetry with respect to any angle

Rotational symmetry with respect to any angle is, in two dimensions, circular symmetry. The fundamental domain is a half-line.

In three dimensions we can distinguish cylindrical symmetry and spherical symmetry (no change when rotating about one axis, or for any rotation). That is, no dependence on the angle using cylindrical coordinates and no dependence on either angle using spherical coordinates. The fundamental domain is a half-plane through the axis, and a radial half-line, respectively. Axisymmetric and axisymmetrical are adjectives which refer to an object having cylindrical symmetry, or axisymmetry (i.e. rotational symmetry with respect to a central axis) like a doughnut (torus). An example of approximate spherical symmetry is the Earth (with respect to density and other physical and chemical properties).

In 4D, continuous or discrete rotational symmetry about a plane corresponds to corresponding 2D rotational symmetry in every perpendicular plane, about the point of intersection. An object can also have rotational symmetry about two perpendicular planes, e.g. if it is the Cartesian product of two rotationally symmetry 2D figures, as in the case of e.g. the duocylinder and various regular duoprisms.

Rotational symmetry with translational symmetry

Arrangement within a primitive cell of 2- and 4-fold rotocenters. A fundamental domain is indicated in yellow.	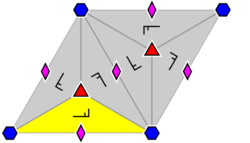Arrangement within a primitive cell of 2-, 3-, and 6-fold rotocenters, alone or in combination (consider the 6-fold symbol as a combination of a 2- and a 3-fold symbol); in the case of 2-fold symmetry only, the shape of the parallelogram can be different. For the case p6, a fundamental domain is indicated in yellow.

2-fold rotational symmetry together with single translational symmetry is one of the Frieze groups. A rotocenter is the fixed, or invariant, point of a rotation.^[3] There are two rotocenters per primitive cell.

Together with double translational symmetry the rotation groups are the following wallpaper groups, with axes per primitive cell:

p2 (2222): 4×2-fold; rotation group of a parallelogrammic, rectangular, and rhombic lattice.
p3 (333): 3×3-fold; not the rotation group of any lattice (every lattice is upside-down the same, but that does not apply for this symmetry); it is e.g. the rotation group of the regular triangular tiling with the equilateral triangles alternatingly colored.
p4 (442): 2×4-fold, 2×2-fold; rotation group of a square lattice.
p6 (632): 1×6-fold, 2×3-fold, 3×2-fold; rotation group of a hexagonal lattice.
2-fold rotocenters (including possible 4-fold and 6-fold), if present at all, form the translate of a lattice equal to the translational lattice, scaled by a factor 1/2. In the case translational symmetry in one dimension, a similar property applies, though the term "lattice" does not apply.
3-fold rotocenters (including possible 6-fold), if present at all, form a regular hexagonal lattice equal to the translational lattice, rotated by 30° (or equivalently 90°), and scaled by a factor ${\tfrac {1}{3}}{\sqrt {3}}$
4-fold rotocenters, if present at all, form a regular square lattice equal to the translational lattice, rotated by 45°, and scaled by a factor ${\tfrac {1}{2}}{\sqrt {2}}$
6-fold rotocenters, if present at all, form a regular hexagonal lattice which is the translate of the translational lattice.

Scaling of a lattice divides the number of points per unit area by the square of the scale factor. Therefore, the number of 2-, 3-, 4-, and 6-fold rotocenters per primitive cell is 4, 3, 2, and 1, respectively, again including 4-fold as a special case of 2-fold, etc.

3-fold rotational symmetry at one point and 2-fold at another one (or ditto in 3D with respect to parallel axes) implies rotation group p6, i.e. double translational symmetry and 6-fold rotational symmetry at some point (or, in 3D, parallel axis). The translation distance for the symmetry generated by one such pair of rotocenters is $2{\sqrt {3}}$ times their distance.

Euclidean plane	Hyperbolic plane
Hexakis triangular tiling, an example of p6, [6,3]⁺, (632) (with colors) and p6m, [6,3], (*632) (without colors); the lines are reflection axes if colors are ignored, and a special kind of symmetry axis if colors are not ignored: reflection reverts the colors. Rectangular line grids in three orientations can be distinguished.	Order 3-7 kisrhombille, an example of [7,3]⁺ (732) symmetry and [7,3], (*732) (without colors)

Related Research Articles

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.

In geometry, an improper rotation is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicular to that axis. Reflection and inversion are each special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation. It is used as a symmetry operation in the context of geometric symmetry, molecular symmetry and crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have improper rotation symmetry.

A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. For each wallpaper there corresponds a group of congruent transformations, with function composition as the group operation. Thus, a wallpaper group is a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations, tiles and physical wallpaper.

In geometry, a glide reflection or transflection is a geometric transformation that consists of a reflection across a hyperplane and a translation ("glide") in a direction parallel to that hyperplane, combined into a single transformation. Because the distances between points are not changed under glide reflection, it is a motion or isometry. When the context is the two-dimensional Euclidean plane, the hyperplane of reflection is a straight line called the glide line or glide axis. When the context is three-dimensional space, the hyperplane of reflection is a plane called the glide plane. The displacement vector of the translation is called the glide vector.

In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible. The distance between any two given points on a rigid body remains constant in time regardless of external forces or moments exerted on it. A rigid body is usually considered as a continuous distribution of mass.

In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups.

In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space $; that is, the transformations of that space that preserve the Euclidean distance between any two points (also called Euclidean transformations). The group depends only on the dimension n of the space, and is commonly denoted E(n) or ISO(n).$

In crystallography, a crystallographic point group is a three dimensional point group whose symmetry operations are compatible with a three dimensional crystallographic lattice. According to the crystallographic restriction it may only contain one-, two-, three-, four- and sixfold rotations or rotoinversions. This reduces the number of crystallographic point groups to 32. These 32 groups are one-and-the-same as the 32 types of morphological (external) crystalline symmetries derived in 1830 by Johann Friedrich Christian Hessel from a consideration of observed crystal forms.

The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold. However, quasicrystals can occur with other diffraction pattern symmetries, such as 5-fold; these were not discovered until 1982 by Dan Shechtman.

In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.

A regular octahedron has 24 rotational symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedron that is dual to an octahedron.

In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dih_n.

In a group, the conjugate by g of h is ghg⁻¹.

In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries (isometries) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O(2), including O(2) itself. Its elements are rotations and reflections, and every such group containing only rotations is a subgroup of the special orthogonal group SO(2), including SO(2) itself. That group is isomorphic to R/Z and the first unitary group, U(1), a group also known as the circle group.

<span class="mw-page-title-main">Rotation around a fixed axis</span> Type of motion

Rotation around a fixed axis or axial rotation is a special case of rotational motion around an axis of rotation fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis of rotation changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will result.

A screw axis is a line that is simultaneously the axis of rotation and the line along which translation of a body occurs. Chasles' theorem shows that each Euclidean displacement in three-dimensional space has a screw axis, and the displacement can be decomposed into a rotation about and a slide along this screw axis.

In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin. This notation is sometimes called international notation, because it was adopted as standard by the International Tables For Crystallography since their first edition in 1935.

In mathematics, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, a 1⁄3 turn rotation of a regular triangle about its center, a reflection of a square across its diagonal, a translation of the Euclidean plane, or a point reflection of a sphere through its center are all symmetry operations. Each symmetry operation is performed with respect to some symmetry element.

<span class="mw-page-title-main">Symmetry (geometry)</span> Geometrical property

In geometry, an object has symmetry if there is an operation or transformation that maps the figure/object onto itself. Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be symmetric under rotation or to have rotational symmetry. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry.

References

↑ Rotational symmetry of Weingarten spheres in homogeneous three-manifolds. By Jos ́e A. G ́alvez, Pablo Mira
↑ Topological Bound States in the Continuum in Arrays of Dielectric Spheres. By Dmitrii N. Maksimov, LV Kirensky Institute of Physics, Krasnoyarsk, Russia
↑ Loeb, A.L. (1971). Color and Symmetry , Wiley-Interscience, New York, p.2. ISBN 9780471543350, OCLC 163904

Weyl, Hermann (1982) [1952]. Symmetry. Princeton: Princeton University Press. ISBN 0-691-02374-3.

External links

Media related to Rotational symmetry at Wikimedia Commons
Rotational Symmetry Examples from Math Is Fun

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Rotational symmetry of Weingarten spheres in homogeneous three-manifolds. By Jos ́e A. G ́alvez, Pablo Mira

[2] Topological Bound States in the Continuum in Arrays of Dielectric Spheres. By Dmitrii N. Maksimov, LV Kirensky Institute of Physics, Krasnoyarsk, Russia

[3] Loeb, A.L. (1971). Color and Symmetry , Wiley-Interscience, New York, p.2. ISBN 9780471543350, OCLC 163904

[1]

[2]

[3]