Duoprism

Last updated December 13, 2023

Set of uniform $p-q$ duoprisms
Type	Prismatic uniform 4-polytopes
Schläfli symbol	${p}\times{q}$
Coxeter-Dynkin diagram
Cells	$p q$ -gonal prisms, $q p$ -gonal prisms
Faces	$pq$ squares, $p q$ -gons, $q p$ -gons
Edges	$2 pq$
Vertices	$pq$
Vertex figure	disphenoid
Symmetry	$[p,2, q]$ , order $4 pq$
Dual	$p-q$ duopyramid
Properties	convex, vertex-uniform

Set of uniform p-p duoprisms
Type	Prismatic uniform 4-polytope
Schläfli symbol	${p}\times{p}$
Coxeter-Dynkin diagram
Cells	$2 p p$ -gonal prisms
Faces	$p 2$ squares, $2 p p$ -gons
Edges	$2 p 2$
Vertices	$p 2$
Symmetry	$[p,2, p] = [2 p,2 +,2 p],$ order $8 p 2$
Dual	$p-p$ duopyramid
Properties	convex, vertex-uniform, Facet-transitive

In geometry of 4 dimensions or higher, a double prism^[1] or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an $n$ -polytope and an $m$ -polytope is an $(n + m)$ -polytope, where $n$ and $m$ are dimensions of 2 (polygon) or higher.

Nomenclature

Four-dimensional duoprisms are considered to be prismatic 4-polytopes. A duoprism constructed from two regular polygons of the same edge length is a uniform duoprism.

A duoprism made of n-polygons and m-polygons is named by prefixing 'duoprism' with the names of the base polygons, for example: a triangular-pentagonal duoprism is the Cartesian product of a triangle and a pentagon.

An alternative, more concise way of specifying a particular duoprism is by prefixing with numbers denoting the base polygons, for example: 3,5-duoprism for the triangular-pentagonal duoprism.

Other alternative names:

q-gonal-p-gonal prism
q-gonal-p-gonal double prism
q-gonal-p-gonal hyperprism

The term duoprism is coined by George Olshevsky, shortened from double prism. John Horton Conway proposed a similar name proprism for product prism, a Cartesian product of two or more polytopes of dimension at least two. The duoprisms are proprisms formed from exactly two polytopes.

Example 16-16 duoprism

Schlegel diagram Projection from the center of one 16-gonal prism, and all but one of the opposite 16-gonal prisms are shown.	net The two sets of 16-gonal prisms are shown. The top and bottom faces of the vertical cylinder are connected when folded together in 4D.

Geometry of 4-dimensional duoprisms

A 4-dimensional uniform duoprism is created by the product of a regular n-sided polygon and a regular m-sided polygon with the same edge length. It is bounded by nm-gonal prisms and mn-gonal prisms. For example, the Cartesian product of a triangle and a hexagon is a duoprism bounded by 6 triangular prisms and 3 hexagonal prisms.

When m and n are identical, the resulting duoprism is bounded by 2n identical n-gonal prisms. For example, the Cartesian product of two triangles is a duoprism bounded by 6 triangular prisms.
When m and n are identically 4, the resulting duoprism is bounded by 8 square prisms (cubes), and is identical to the tesseract.

The m-gonal prisms are attached to each other via their m-gonal faces, and form a closed loop. Similarly, the n-gonal prisms are attached to each other via their n-gonal faces, and form a second loop perpendicular to the first. These two loops are attached to each other via their square faces, and are mutually perpendicular.

As m and n approach infinity, the corresponding duoprisms approach the duocylinder. As such, duoprisms are useful as non-quadric approximations of the duocylinder.

Nets

3-3
3-4	4-4
3-5	4-5	5-5
3-6	4-6	5-6	6-6
3-7	4-7	5-7	6-7	7-7
3-8	4-8	5-8	6-8	7-8	8-8
3-9	4-9	5-9	6-9	7-9	8-9	9-9
3-10	4-10	5-10	6-10	7-10	8-10	9-10	10-10

Perspective projections

A cell-centered perspective projection makes a duoprism look like a torus, with two sets of orthogonal cells, p-gonal and q-gonal prisms.

Schlegel diagrams
6-prism	6-6 duoprism

A hexagonal prism, projected into the plane by perspective, centered on a hexagonal face, looks like a double hexagon connected by (distorted) squares. Similarly a 6-6 duoprism projected into 3D approximates a torus, hexagonal both in plan and in section.

The p-q duoprisms are identical to the q-p duoprisms, but look different in these projections because they are projected in the center of different cells.

Schlegel diagrams
3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

Orthogonal projections

Vertex-centered orthogonal projections of p-p duoprisms project into [2n] symmetry for odd degrees, and [n] for even degrees. There are n vertices projected into the center. For 4,4, it represents the A₃ Coxeter plane of the tesseract. The 5,5 projection is identical to the 3D rhombic triacontahedron.

Orthogonal projection wireframes of p-p duoprisms
Odd
3-3		5-5		7-7		9-9

[3]	[6]	[5]	[10]	[7]	[14]	[9]	[18]
Even
4-4 (tesseract)		6-6		8-8		10-10

[4]	[8]	[6]	[12]	[8]	[16]	[10]	[20]

Related polytopes

A stereographic projection of a rotating duocylinder, divided into a checkerboard surface of squares from the {4,4|n} skew polyhedron Duocylinder ridge animated.gif — A stereographic projection of a rotating duocylinder, divided into a checkerboard surface of squares from the {4,4|n} skew polyhedron

The regular skew polyhedron, {4,4|n}, exists in 4-space as the n² square faces of a n-n duoprism, using all 2n² edges and n² vertices. The 2nn-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are not regular.)

Duoantiprism

Like the antiprisms as alternated prisms, there is a set of 4-dimensional duoantiprisms: 4-polytopes that can be created by an alternation operation applied to a duoprism. The alternated vertices create nonregular tetrahedral cells, except for the special case, the 4-4 duoprism (tesseract) which creates the uniform (and regular) 16-cell. The 16-cell is the only convex uniform duoantiprism.

The duoprisms , t_0,1,2,3{p,2,q}, can be alternated into , ht_0,1,2,3{p,2,q}, the "duoantiprisms", which cannot be made uniform in general. The only convex uniform solution is the trivial case of p=q=2, which is a lower symmetry construction of the tesseract , t_0,1,2,3{2,2,2}, with its alternation as the 16-cell, , s{2}s{2}.

The only nonconvex uniform solution is p=5, q=5/3, ht_0,1,2,3{5,2,5/3}, , constructed from 10 pentagonal antiprisms, 10 pentagrammic crossed-antiprisms, and 50 tetrahedra, known as the great duoantiprism (gudap).^[2]^[3]

Ditetragoltriates

Also related are the ditetragoltriates or octagoltriates, formed by taking the octagon (considered to be a ditetragon or a truncated square) to a p-gon. The octagon of a p-gon can be clearly defined if one assumes that the octagon is the convex hull of two perpendicular rectangles; then the p-gonal ditetragoltriate is the convex hull of two p-p duoprisms (where the p-gons are similar but not congruent, having different sizes) in perpendicular orientations. The resulting polychoron is isogonal and has 2p p-gonal prisms and p² rectangular trapezoprisms (a cube with D_2d symmetry) but cannot be made uniform. The vertex figure is a triangular bipyramid.

Double antiprismoids

Like the duoantiprisms as alternated duoprisms, there is a set of p-gonal double antiprismoids created by alternating the 2p-gonal ditetragoltriates, creating p-gonal antiprisms and tetrahedra while reinterpreting the non-corealmic triangular bipyramidal spaces as two tetrahedra. The resulting figure is generally not uniform except for two cases: the grand antiprism and its conjugate, the pentagrammic double antiprismoid (with p = 5 and 5/3 respectively), represented as the alternation of a decagonal or decagrammic ditetragoltriate. The vertex figure is a variant of the sphenocorona.

k_22 polytopes

The 3-3 duoprism, -1₂₂, is first in a dimensional series of uniform polytopes, expressed by Coxeter as k₂₂ series. The 3-3 duoprism is the vertex figure for the second, the birectified 5-simplex. The fourth figure is a Euclidean honeycomb, 2₂₂, and the final is a paracompact hyperbolic honeycomb, 3₂₂, with Coxeter group [3^2,2,3], ${\bar {T}}_{7}$ . Each progressive uniform polytope is constructed from the previous as its vertex figure.

k₂₂ figures in n dimensions
Space	Finite			Euclidean	Hyperbolic
n	4	5	6	7	8
Coxeter group	A₂A₂	E₆	${\tilde {E}}_{6}$ =E₆⁺	${\bar {T}}_{7}$ =E₆⁺⁺
Coxeter diagram
Symmetry	[[3^2,2,-1]]	[[3^2,2,0]]	[[3^2,2,1]]	[[3^2,2,2]]	[[3^2,2,3]]
Order	72	1440	103,680	∞
Graph				∞	∞
Name	−1₂₂	0₂₂	1₂₂	2₂₂	3₂₂

Notes

↑ The Fourth Dimension Simply Explained, Henry P. Manning, Munn & Company, 1910, New York. Available from the University of Virginia library. Also accessible online: The Fourth Dimension Simply Explained —contains a description of duoprisms (double prisms) and duocylinders (double cylinders). Googlebook
↑ Jonathan Bowers - Miscellaneous Uniform Polychora 965. Gudap
↑ http://www.polychora.com/12GudapsMovie.gif Animation of cross sections

Related Research Articles

In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.

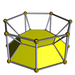
In geometry, a prism is a polyhedron comprising an $n$ -sided polygon base, a second base which is a translated copy of the first, and $n$ other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.

<span class="mw-page-title-main">Schläfli symbol</span> Notation that defines regular polytopes and tessellations

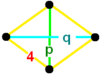
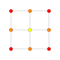
In geometry, the Schläfli symbol is a notation of the form $that defines regular polytopes and tessellations.$

In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

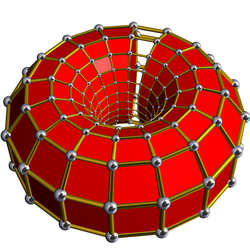
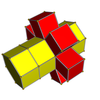
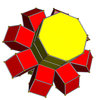
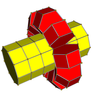
In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

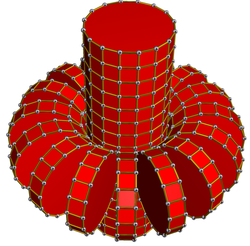
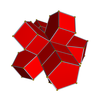
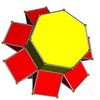
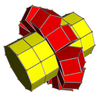
In four-dimensional geometry, a cantellated tesseract is a convex uniform 4-polytope, being a cantellation of the regular tesseract.

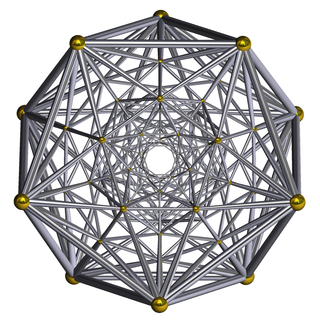
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope (4-dimensional uniform polytope) bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polytope, discovered in 1965 by Conway and Guy. Topologically, under its highest symmetry, the pentagonal antiprisms have D_5d symmetry and there are two types of tetrahedra, one with S₄ symmetry and one with C_s symmetry.

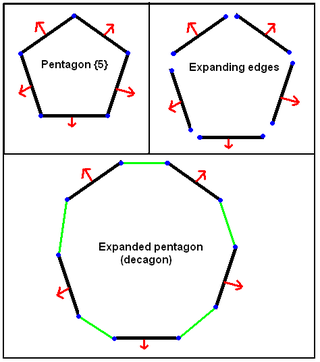
In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements. Equivalently this operation can be imagined by keeping facets in the same position but reducing their size.

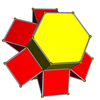
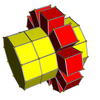
In four-dimensional geometry, a cantellated 24-cell is a convex uniform 4-polytope, being a cantellation of the regular 24-cell.

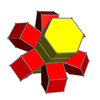
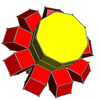
In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.

In geometry, a skew polygon is a polygon whose vertices are not all coplanar. Skew polygons must have at least four vertices. The interior surface of such a polygon is not uniquely defined.

In six-dimensional geometry, a uniform 6-polytope is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform 5-polytopes.

In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons.

In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.

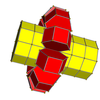
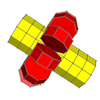
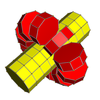
In geometry of 4 dimensions or higher, a proprism is a polytope resulting from the Cartesian product of two or more polytopes, each of two dimensions or higher. The term was coined by John Horton Conway for product prism. The dimension of the space of a proprism equals the sum of the dimensions of all its product elements. Proprisms are often seen as k-face elements of uniform polytopes.

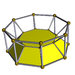
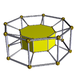
In four-dimensional geometry, a prismatic uniform 4-polytope is a uniform 4-polytope with a nonconnected Coxeter diagram symmetry group. These figures are analogous to the set of prisms and antiprism uniform polyhedra, but add a third category called duoprisms, constructed as a product of two regular polygons.

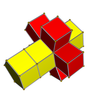
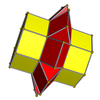
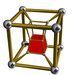
In the geometry of 4 dimensions, the 3-3 duoprism or triangular duoprism is a four-dimensional convex polytope. It can be constructed as the Cartesian product of two triangles and is the simplest of an infinite family of four-dimensional polytopes constructed as Cartesian products of two polygons, the duoprisms.

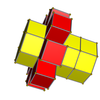
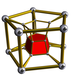
In geometry of 4 dimensions, a 3-4 duoprism, the second smallest p-q duoprism, is a 4-polytope resulting from the Cartesian product of a triangle and a square.

In geometry, the great duoantiprism is the only uniform star-duoantiprism solution $p = 5,$ $q = 5 / 3,$ in 4-dimensional geometry. It has Schläfli symbol ${5}\otimes{5/3},$ $s{5}s{5/3}$ or $ht 0,1,2,3 {5,2,5/3},$ Coxeter diagram , constructed from 10 pentagonal antiprisms, 10 pentagrammic crossed-antiprisms, and 50 tetrahedra.

References

Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] The Fourth Dimension Simply Explained, Henry P. Manning, Munn & Company, 1910, New York. Available from the University of Virginia library. Also accessible online: The Fourth Dimension Simply Explained —contains a description of duoprisms (double prisms) and duocylinders (double cylinders). Googlebook

[2] Jonathan Bowers - Miscellaneous Uniform Polychora 965. Gudap

[3] ttp://www.polychora.com/12GudapsMovie.gif Animation of cross sections

[1]

[2]

[3]