Coxeter notation

Fundamental domains of reflective 3D point groups

, [ ] = [1] C1v	, [2] C2v	, [3] C3v	, [4] C4v	, [5] C5v	, [6] C6v
Order 2	Order 4	Order 6	Order 8	Order 10	Order 12
[2] = [2,1] D1h	[2,2] D2h	[2,3] D3h	[2,4] D4h	[2,5] D5h	[2,6] D6h
Order 4	Order 8	Order 12	Order 16	Order 20	Order 24
, [3,3], Td		, [4,3], Oh		, [5,3], Ih
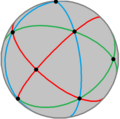Order 24		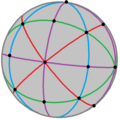Order 48		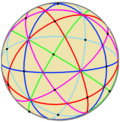Order 120
Coxeter notation expresses Coxeter groups as a list of branch orders of a Coxeter diagram, like the polyhedral groups, = [p,q]. Dihedral groups, , can be expressed as a product [ ]×[n] or in a single symbol with an explicit order 2 branch, [2,n].

In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.

Reflectional groups

Further information: Point group

For Coxeter groups, defined by pure reflections, there is a direct correspondence between the bracket notation and Coxeter-Dynkin diagram. The numbers in the bracket notation represent the mirror reflection orders in the branches of the Coxeter diagram. It uses the same simplification, suppressing 2s between orthogonal mirrors.

The Coxeter notation is simplified with exponents to represent the number of branches in a row for linear diagram. So the A_n group is represented by [3ⁿ⁻¹], to imply n nodes connected by n−1 order-3 branches. Example A₂ = [3,3] = [3²] or [3^1,1] represents diagrams or .

Coxeter initially represented bifurcating diagrams with vertical positioning of numbers, but later abbreviated with an exponent notation, like [...,3^p,q] or [3^p,q,r], starting with [3^1,1,1] or [3,3^1,1] = or as D₄. Coxeter allowed for zeros as special cases to fit the A_n family, like A₃ = [3,3,3,3] = [3^4,0,0] = [3^4,0] = [3^3,1] = [3^2,2], like = = .

Coxeter groups formed by cyclic diagrams are represented by parentheseses inside of brackets, like [(p,q,r)] = for the triangle group (p q r). If the branch orders are equal, they can be grouped as an exponent as the length the cycle in brackets, like [(3,3,3,3)] = [3^[4]], representing Coxeter diagram or . can be represented as [3,(3,3,3)] or [3,3^[3]].

More complicated looping diagrams can also be expressed with care. The paracompact Coxeter group can be represented by Coxeter notation [(3,3,(3),3,3)], with nested/overlapping parentheses showing two adjacent [(3,3,3)] loops, and is also represented more compactly as [3^[ ]×[ ]], representing the rhombic symmetry of the Coxeter diagram. The paracompact complete graph diagram or , is represented as [3^[3,3]] with the superscript [3,3] as the symmetry of its regular tetrahedron coxeter diagram.

Finite groups Rank Group symbol Bracket notation Coxeter diagram 2 A2 [3] 2 B2 [4] 2 H2 [5] 2 G2 [6] 2 I2(p) [p] 3 Ih, H3 [5,3] 3 Td, A3 [3,3] 3 Oh, B3 [4,3] 4 A4 [3,3,3] 4 B4 [4,3,3] 4 D4 [31,1,1] 4 F4 [3,4,3] 4 H4 [5,3,3] n An [3n−1] .. n Bn [4,3n−2] ... n Dn [3n−3,1,1] ... 6 E6 [32,2,1] 7 E7 [33,2,1] 8 E8 [34,2,1]

Affine groups Group symbol Bracket notation Coxeter diagram ${\displaystyle {\tilde {I}}_{1},{\tilde {A}}_{1}}$ [∞] ${\displaystyle {\tilde {A}}_{2}}$ [3[3]] ${\displaystyle {\tilde {C}}_{2}}$ [4,4] ${\displaystyle {\tilde {G}}_{2}}$ [6,3] ${\displaystyle {\tilde {A}}_{3}}$ [3[4]] ${\displaystyle {\tilde {B}}_{3}}$ [4,31,1] ${\displaystyle {\tilde {C}}_{3}}$ [4,3,4] ${\displaystyle {\tilde {A}}_{4}}$ [3[5]] ${\displaystyle {\tilde {B}}_{4}}$ [4,3,31,1] ${\displaystyle {\tilde {C}}_{4}}$ [4,3,3,4] ${\displaystyle {\tilde {D}}_{4}}$ [ 31,1,1,1] ${\displaystyle {\tilde {F}}_{4}}$ [3,4,3,3] ${\displaystyle {\tilde {A}}_{n}}$ [3[n+1]] ... or ... ${\displaystyle {\tilde {B}}_{n}}$ [4,3n−3,31,1] ... ${\displaystyle {\tilde {C}}_{n}}$ [4,3n−2,4] ... ${\displaystyle {\tilde {D}}_{n}}$ [ 31,1,3n−4,31,1] ... ${\displaystyle {\tilde {E}}_{6}}$ [32,2,2] ${\displaystyle {\tilde {E}}_{7}}$ [33,3,1] ${\displaystyle {\tilde {E}}_{8}=E_{9}}$ [35,2,1]

Hyperbolic groups Group symbol Bracket notation Coxeter diagram [p,q] with 2(p + q) < pq [(p,q,r)] with ${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}<1}$ ${\displaystyle {\overline {BH}}_{3}}$ [4,3,5] ${\displaystyle {\overline {K}}_{3}}$ [5,3,5] ${\displaystyle {\overline {J}}_{3},{\tilde {H}}_{3}}$ [3,5,3] ${\displaystyle {\overline {DH}}_{3}}$ [5,31,1] ${\displaystyle {\widehat {AB}}_{3}}$ [(3,3,3,4)]   ${\displaystyle {\widehat {AH}}_{3}}$ [(3,3,3,5)]   ${\displaystyle {\widehat {BB}}_{3}}$ [(3,4,3,4)] ${\displaystyle {\widehat {BH}}_{3}}$ [(3,4,3,5)] ${\displaystyle {\widehat {HH}}_{3}}$ [(3,5,3,5)] ${\displaystyle {\overline {H}}_{4},{\tilde {H}}_{4},H_{5}}$ [3,3,3,5] ${\displaystyle {\overline {BH}}_{4}}$ [4,3,3,5] ${\displaystyle {\overline {K}}_{4}}$ [5,3,3,5] ${\displaystyle {\overline {DH}}_{4}}$ [5,3,31,1] ${\displaystyle {\widehat {AF}}_{4}}$ [(3,3,3,3,4)]

For the affine and hyperbolic groups, the subscript is one less than the number of nodes in each case, since each of these groups was obtained by adding a node to a finite group's diagram.

Unconnected groups

The Coxeter diagram usually leaves order-2 branches undrawn, but the bracket notation includes an explicit 2 to connect the subgraphs. So the Coxeter diagram = A₂×A₂ = 2A₂ can be represented by [3]×[3] = [3]² = [3,2,3]. Sometimes explicit 2-branches may be included either with a 2 label, or with a line with a gap: or , as an identical presentation as [3,2,3].

Rank and dimension

Coxeter point group rank is equal to the number of nodes which is also equal to the dimension. A single mirror exists in 1-dimension, [ ], , while in 2-dimensions [1], or [ ]×[ ]⁺. The 1 is a place-holder, not an actual branch order, but a marker for an orthogonal inactive mirror. The notation [n,1], represents a rank 3 group, as [n]×[ ]⁺ or . Similarly, [1,1] as [ ]×[ ]⁺×[ ]⁺ or order 2 and [1,1]⁺ as [ ]⁺×[ ]⁺×[ ]⁺ or , order 1!

Subgroups

Coxeter's notation represents rotational/translational symmetry by adding a ⁺ superscript operator outside the brackets, [X]⁺ which cuts the order of the group [X] in half, thus an index 2 subgroup. This operator implies an even number of operators must be applied, replacing reflections with rotations (or translations). When applied to a Coxeter group, this is called a direct subgroup because what remains are only direct isometries without reflective symmetry.

The ⁺ operators can also be applied inside of the brackets, like [X,Y⁺] or [X,(Y,Z)⁺], and creates "semidirect" subgroups that may include both reflective and nonreflective generators. Semidirect subgroups can only apply to Coxeter group subgroups that have even order branches adjacent to it. Elements by parentheses inside of a Coxeter group can be give a ⁺ superscript operator, having the effect of dividing adjacent ordered branches into half order, thus is usually only applied with even numbers. For example, [4,3⁺] and [4,(3,3)⁺] ().

If applied with adjacent odd branch, it doesn't create a subgroup of index 2, but instead creates overlapping fundamental domains, like [5,1⁺] = [5/2], which can define doubly wrapped polygons like a pentagram, {5/2}, and [5,3⁺] relates to Schwarz triangle [5/2,3], density 2.

Examples on Rank 2 groups

Group		Order	Generators	Subgroup		Order	Generators	Notes
[p]		2p	{0,1}	[p]+		p	{01}	Direct subgroup
[2p+] = [2p]+		2p	{01}	[2p+]+ = [2p]+2 = [p]+		p	{0101}
[2p]		4p	{0,1}	[1+,2p] = [p]	= =	2p	{101,1}	Half subgroups
				[2p,1+] = [p]	= =		{0,010}
				[1+,2p,1+] = [2p]+2 = [p]+	= =	p	{0101}	Quarter group

Groups without neighboring ⁺ elements can be seen in ringed nodes Coxeter-Dynkin diagram for uniform polytopes and honeycomb are related to hole nodes around the ⁺ elements, empty circles with the alternated nodes removed. So the snub cube, has symmetry [4,3]⁺ (), and the snub tetrahedron, has symmetry [4,3⁺] (), and a demicube, h{4,3} = {3,3} ( or = ) has symmetry [1⁺,4,3] = [3,3] ( or = = ).

Note: Pyritohedral symmetry can be written as , separating the graph with gaps for clarity, with the generators {0,1,2} from the Coxeter group , producing pyritohedral generators {0,12}, a reflection and 3-fold rotation. And chiral tetrahedral symmetry can be written as or , [1⁺,4,3⁺] = [3,3]⁺, with generators {12,0120}.

Halving subgroups and extended groups

Further information: § Extended_symmetry

Example halving operations

[1,4,1] = [4]	= = [1+,4,1]=[2]=[ ]×[ ]
= = [1,4,1+]=[2]=[ ]×[ ]	= = = [1+,4,1+] = [2]+

Johnson extends the ⁺ operator to work with a placeholder 1⁺ nodes, which removes mirrors, doubling the size of the fundamental domain and cuts the group order in half. ^[1] In general this operation only applies to individual mirrors bounded by even-order branches. The 1 represents a mirror so [2p] can be seen as [2p,1], [1,2p], or [1,2p,1], like diagram or , with 2 mirrors related by an order-2p dihedral angle. The effect of a mirror removal is to duplicate connecting nodes, which can be seen in the Coxeter diagrams: = , or in bracket notation:[1⁺,2p, 1] = [1,p,1] = [p].

Each of these mirrors can be removed so h[2p] = [1⁺,2p,1] = [1,2p,1⁺] = [p], a reflective subgroup index 2. This can be shown in a Coxeter diagram by adding a ⁺ symbol above the node: = = .

If both mirrors are removed, a quarter subgroup is generated, with the branch order becoming a gyration point of half the order:

q[2p] = [1⁺,2p,1⁺] = [p]⁺, a rotational subgroup of index 4. = = = = .

For example, (with p=2): [4,1⁺] = [1⁺,4] = [2] = [ ]×[ ], order 4. [1⁺,4,1⁺] = [2]⁺, order 2.

The opposite to halving is doubling ^[2] which adds a mirror, bisecting a fundamental domain, and doubling the group order.

[[p]] = [2p]

Halving operations apply for higher rank groups, like tetrahedral symmetry is a half group of octahedral group: h[4,3] = [1⁺,4,3] = [3,3], removing half the mirrors at the 4-branch. The effect of a mirror removal is to duplicate all connecting nodes, which can be seen in the Coxeter diagrams: = , h[2p,3] = [1⁺,2p,3] = [(p,3,3)].

If nodes are indexed, half subgroups can be labeled with new mirrors as composites. Like , generators {0,1} has subgroup = , generators {1,010}, where mirror 0 is removed, and replaced by a copy of mirror 1 reflected across mirror 0. Also given , generators {0,1,2}, it has half group = , generators {1,2,010}.

Doubling by adding a mirror also applies in reversing the halving operation: [[3,3]] = [4,3], or more generally [[(q,q,p)]] = [2p,q].

Tetrahedral symmetry	Octahedral symmetry
Td, [3,3] = [1+,4,3] = = (Order 24)	Oh, [4,3] = [[3,3]] (Order 48)

Radical subgroups

A radical subgroup is similar to an alternation, but removes the rotational generators.

Johnson also added an asterisk or star * operator for "radical" subgroups, ^[3] that acts similar to the ⁺ operator, but removes rotational symmetry. The index of the radical subgroup is the order of the removed element. For example, [4,3*] ≅ [2,2]. The removed [3] subgroup is order 6 so [2,2] is an index 6 subgroup of [4,3].

The radical subgroups represent the inverse operation to an extended symmetry operation. For example, [4,3*] ≅ [2,2], and in reverse [2,2] can be extended as [3[2,2]] ≅ [4,3]. The subgroups can be expressed as a Coxeter diagram: or ≅ . The removed node (mirror) causes adjacent mirror virtual mirrors to become real mirrors.

If [4,3] has generators {0,1,2}, [4,3⁺], index 2, has generators {0,12}; [1⁺,4,3] ≅ [3,3], index 2 has generators {010,1,2}; while radical subgroup [4,3*] ≅ [2,2], index 6, has generators {01210, 2, (012)³}; and finally [1⁺,4,3*], index 12 has generators {0(12)²0, (012)²01}.

Trionic subgroups

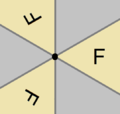
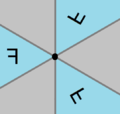
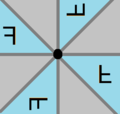
Rank 2 example, [6] trionic subgroups with 3 colors of mirror lines

Example on octahedral symmetry: [4,3 ] = [2,4].

Example trionic subgroup on hexagonal symmetry [6,3] maps onto a larger [6,3] symmetry.

Rank 3

Example trionic subgroups on octagonal symmetry [8,3] maps onto larger [4,8] symmetries.

Rank 4

A trionic subgroup is an index 3 subgroup. Johnson defines a trionic subgroup with operator ⅄, index 3. For rank 2 Coxeter groups, [3], the trionic subgroup, [3^⅄] is [ ], a single mirror. And for [3p], the trionic subgroup is [3p]^⅄ ≅ [p]. Given , with generators {0,1}, has 3 trionic subgroups. They can be differentiated by putting the ⅄ symbol next to the mirror generator to be removed, or on a branch for both: [3p,1^⅄] = = , = , and [3p^⅄] = = with generators {0,10101}, {01010,1}, or {101,010}.

Trionic subgroups of tetrahedral symmetry: [3,3]^⅄ ≅ [2⁺,4], relating the symmetry of the regular tetrahedron and tetragonal disphenoid.

For rank 3 Coxeter groups, [p,3], there is a trionic subgroup [p,3^⅄] ≅ [p/2,p], or = . For example, the finite group [4,3^⅄] ≅ [2,4], and Euclidean group [6,3^⅄] ≅ [3,6], and hyperbolic group [8,3^⅄] ≅ [4,8].

An odd-order adjacent branch, p, will not lower the group order, but create overlapping fundamental domains. The group order stays the same, while the density increases. For example, the icosahedral symmetry, [5,3], of the regular polyhedra icosahedron becomes [5/2,5], the symmetry of 2 regular star polyhedra. It also relates the hyperbolic tilings {p,3}, and star hyperbolic tilings {p/2,p}

For rank 4, [q,2p,3^⅄] = [2p,((p,q,q))], = .

For example, [3,4,3^⅄] = [4,3,3], or = , generators {0,1,2,3} in [3,4,3] with the trionic subgroup [4,3,3] generators {0,1,2,32123}. For hyperbolic groups, [3,6,3^⅄] = [6,3^[3]], and [4,4,3^⅄] = [4,4,4].

Trionic subgroups of tetrahedral symmetry

[3,3] ≅ [2 ,4] as one of 3 sets of 2 orthogonal mirrors in stereographic projection. The red, green, and blue represent 3 sets of mirrors, and the gray lines are removed mirrors, leaving 2-fold gyrations (purple diamonds).

Trionic relations of [3,3]

Johnson identified two specific trionic subgroups ^[4] of [3,3], first an index 3 subgroup [3,3]^⅄ ≅ [2⁺,4], with [3,3] ( = = ) generators {0,1,2}. It can also be written as [(3,3,2^⅄)] () as a reminder of its generators {02,1}. This symmetry reduction is the relationship between the regular tetrahedron and the tetragonal disphenoid, represent a stretching of a tetrahedron perpendicular to two opposite edges.

Secondly he identifies a related index 6 subgroup [3,3]^Δ or [(3,3,2^⅄)]⁺ (), index 3 from [3,3]⁺ ≅ [2,2]⁺, with generators {02,1021}, from [3,3] and its generators {0,1,2}.

These subgroups also apply within larger Coxeter groups with [3,3] subgroup with neighboring branches all even order.

Trionic subgroup relations of [3,3,4]

For example, [(3,3)⁺,4], [(3,3)^⅄,4], and [(3,3)^Δ,4] are subgroups of [3,3,4], index 2, 3 and 6 respectively. The generators of [(3,3)^⅄,4] ≅ [[4,2,4]] ≅ [8,2⁺,8], order 128, are {02,1,3} from [3,3,4] generators {0,1,2,3}. And [(3,3)^Δ,4] ≅ [[4,2⁺,4]], order 64, has generators {02,1021,3}. As well, [3^⅄,4,3^⅄] ≅ [(3,3)^⅄,4].

Also related [3^1,1,1] = [3,3,4,1⁺] has trionic subgroups: [3^1,1,1]^⅄ = [(3,3)^⅄,4,1⁺], order 64, and 1=[3^1,1,1]^Δ = [(3,3)^Δ,4,1⁺] ≅ [[4,2⁺,4]]⁺, order 32.

Central inversion

A 2D central inversion is a 180 degree rotation, [2]

A central inversion, order 2, is operationally differently by dimension. The group [ ]ⁿ = [2ⁿ⁻¹] represents n orthogonal mirrors in n-dimensional space, or an n-flat subspace of a higher dimensional space. The mirrors of the group [2ⁿ⁻¹] are numbered ${\displaystyle 0\dots n-1}$. The order of the mirrors doesn't matter in the case of an inversion. The matrix of a central inversion is ${\displaystyle -I}$, the Identity matrix with negative one on the diagonal.

From that basis, the central inversion has a generator as the product of all the orthogonal mirrors. In Coxeter notation this inversion group is expressed by adding an alternation ⁺ to each 2 branch. The alternation symmetry is marked on Coxeter diagram nodes as open nodes.

A Coxeter-Dynkin diagram can be marked up with explicit 2 branches defining a linear sequence of mirrors, open-nodes, and shared double-open nodes to show the chaining of the reflection generators.

For example, [2⁺,2] and [2,2⁺] are subgroups index 2 of [2,2], , and are represented as (or ) and (or ) with generators {01,2} and {0,12} respectively. Their common subgroup index 4 is [2⁺,2⁺], and is represented by (or ), with the double-open marking a shared node in the two alternations, and a single rotoreflection generator {012}.

Dimension	Coxeter notation	Order	Coxeter diagram	Operation	Generator
2	[2]+	2		180° rotation, C2	{01}
3	[2+,2+]	2		rotoreflection, Ci or S2	{012}
4	[2+,2+,2+]	2		double rotation	{0123}
5	[2+,2+,2+,2+]	2		double rotary reflection	{01234}
6	[2+,2+,2+,2+,2+]	2		triple rotation	{012345}
7	[2+,2+,2+,2+,2+,2+]	2		triple rotary reflection	{0123456}

Rotations and rotary reflections

Rotations and rotary reflections are constructed by a single single-generator product of all the reflections of a prismatic group, [2p]×[2q]×... where gcd(p,q,...)=1, they are isomorphic to the abstract cyclic group Z_n, of order n=2pq.

The 4-dimensional double rotations, [2p⁺,2⁺,2q⁺] (with gcd(p,q)=1), which include a central group, and are expressed by Conway as ±[C_p×C_q], ^[5] order 2pq. From Coxeter diagram , generators {0,1,2,3}, requires two generator for [2p⁺,2⁺,2q⁺], as {0123,0132}. Half groups, [2p⁺,2⁺,2q⁺]⁺, or cyclic graph, [(2p⁺,2⁺,2q⁺,2⁺)], expressed by Conway is [C_p×C_q], order pq, with one generator, like {0123}.

If there is a common factor f, the double rotation can be written as 1⁄f[2pf⁺,2⁺,2qf⁺] (with gcd(p,q)=1), generators {0123,0132}, order 2pqf. For example, p=q=1, f=2, 1⁄2[4⁺,2⁺,4⁺] is order 4. And 1⁄f[2pf⁺,2⁺,2qf⁺]⁺, generator {0123}, is order pqf. For example, 1⁄2[4⁺,2⁺,4⁺]⁺ is order 2, a central inversion.

In general a n-rotation group, [2p₁⁺,2,2p₂⁺,2,...,p_n⁺] may require up to n generators if gcd(p₁,..,p_n)>1, as a product of all mirrors, and then swapping sequential pairs. The half group, [2p₁⁺,2,2p₂⁺,2,...,p_n⁺]⁺ has generators squared. n-rotary reflections are similar.

Examples

Dimension	Coxeter notation	Order	Coxeter diagram	Operation	Generators	Direct subgroup
2	[2p]+	2p		Rotation	{01}	[2p]+2 = [p]+	Simple rotation: [2p]+2 = [p]+ order p
3	[2p+,2+]			rotary reflection	{012}	[2p+,2+]+ = [p]+
4	[2p+,2+,2+]			double rotation	{0123}	[2p+,2+,2+]+ = [p]+
5	[2p+,2+,2+,2+]			double rotary reflection	{01234}	[2p+,2+,2+,2+]+ = [p]+
6	[2p+,2+,2+,2+,2+]			triple rotation	{012345}	[2p+,2+,2+,2+,2+]+ = [p]+
7	[2p+,2+,2+,2+,2+,2+]			triple rotary reflection	{0123456}	[2p+,2+,2+,2+,2+,2+]+ = [p]+
4	[2p+,2+,2q+]	2pq		double rotation	{0123, 0132}	[2p+,2+,2q+]+	Double rotation: [2p+,2+,2q+]+ order pq
5	[2p+,2+,2q+,2+]			double rotary reflection	{01234, 01243}	[2p+,2+,2q+,2+]+
6	[2p+,2+,2q+,2+,2+]			triple rotation	{012345, 012354, 013245}	[2p+,2+,2q+,2+,2+]+
7	[2p+,2+,2q+,2+,2+,2+]			triple rotary reflection	{0123456, 0123465, 0124356, 0124356}	[2p+,2+,2q+,2+,2+,2+]+
6	[2p+,2+,2q+,2+,2r+]	2pqr		triple rotation	{012345, 012354, 013245}	[2p+,2+,2q+,2+,2r+]+	Triple rotation: [2p+,2+,2q+,2+,2r+]+ order pqr
7	[2p+,2+,2q+,2+,2r+,2+]			triple rotary reflection	{0123456, 0123465, 0124356, 0213456}	[2p+,2+,2q+,2+,2r+,2+]+

Commutator subgroups

Hasse diagram subgroups of [4,4], down to its commutator subgroup, index 8

Simple groups with only odd-order branch elements have only a single rotational/translational subgroup of order 2, which is also the commutator subgroup, examples [3,3]⁺, [3,5]⁺, [3,3,3]⁺, [3,3,5]⁺. For other Coxeter groups with even-order branches, the commutator subgroup has index 2^c, where c is the number of disconnected subgraphs when all the even-order branches are removed. ^[6]

For example, [4,4] has three independent nodes in the Coxeter diagram when the 4s are removed, so its commutator subgroup is index 2³, and can have different representations, all with three ⁺ operators: [4⁺,4⁺]⁺, [1⁺,4,1⁺,4,1⁺], [1⁺,4,4,1⁺]⁺, or [(4⁺,4⁺,2⁺)]. A general notation can be used with +c as a group exponent, like [4,4]⁺³.

Example subgroups

Rank 2 example subgroups

Dihedral symmetry groups with even-orders have a number of subgroups. This example shows two generator mirrors of [4] in red and green, and looks at all subgroups by halfing, rank-reduction, and their direct subgroups. The group [4], has two mirror generators 0, and 1. Each generate two virtual mirrors 101 and 010 by reflection across the other.

Subgroups of [4]
Index	1	2 (half)		4 (Rank-reduction)
Diagram
Coxeter	[1,4,1] = [4]	= = [1+,4,1] = [1+,4] = [2]	= = [1,4,1+] = [4,1+] = [2]	[2,1+] = [1] = [ ]	[1+,2] = [1] = [ ]
Generators	{0,1}	{101,1}	{0,010}	{0}	{1}
Direct subgroups
Index	2	4		8
Diagram
Coxeter	[4]+	= = = [4]+2 = [1+,4,1+] = [2]+		[ ]+
Generators	{01}	{(01)2}		{02} = {12} = {(01)4} = { }

Rank 3 Euclidean example subgroups

The [4,4] group has 15 small index subgroups. This table shows them all, with a yellow fundamental domain for pure reflective groups, and alternating white and blue domains which are paired up to make rotational domains. Cyan, red, and green mirror lines correspond to the same colored nodes in the Coxeter diagram. Subgroup generators can be expressed as products of the original 3 mirrors of the fundamental domain, {0,1,2}, corresponding to the 3 nodes of the Coxeter diagram, . A product of two intersecting reflection lines makes a rotation, like {012}, {12}, or {02}. Removing a mirror causes two copies of neighboring mirrors, across the removed mirror, like {010}, and {212}. Two rotations in series cut the rotation order in half, like {0101} or {(01)²}, {1212} or {(02)²}. A product of all three mirrors creates a transreflection, like {012} or {120}.

Small index subgroups of [4,4]
Index	1	2			4
Diagram
Coxeter	[1,4,1,4,1] = [4,4]	[1+,4,4] =	[4,4,1+] =	[4,1+,4] =	[1+,4,4,1+] =	[4+,4+]
Generators	{0,1,2}	{010,1,2}	{0,1,212}	{0,101,121,2}	{010,1,212,20102}	{(01)2,(12)2,012,120}
Orbifold	*442			*2222		22×
Semidirect subgroups
Index		2			4
Diagram
Coxeter		[4,4+]	[4+,4]	[(4,4,2+)] =	[4,1+,4,1+] = =	[1+,4,1+,4] = =
Generators		{0,12}	{01,2}	{02,1,212}	{0,101,(12)2}	{(01)2,121,2}
Orbifold		4*2		2*22
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[4,4]+ =	[4,4+]+ =	[4+,4]+ =	[(4,4,2+)]+ =	[4,4]+3 = [(4+,4+,2+)] = [1+,4,1+,4,1+] = [4+,4+]+ = = = =
Generators	{01,12}	{(01)2,12}	{01,(12)2}	{02,(01)2,(12)2}	{(01)2,(12)2,2(01)22}
Orbifold	442			2222
Radical subgroups
Index		8		16
Diagram
Coxeter		[4,4*] =	[4*,4] =	[4,4*]+ =	[4*,4]+ =
Orbifold		*2222		2222

Hyperbolic example subgroups

The same set of 15 small subgroups exists on all triangle groups with even order elements, like [6,4] in the hyperbolic plane:

Small index subgroups of [6,4]
Index	1	2			4
Diagram
Coxeter	[1,6,1,4,1] = [6,4]	[1+,6,4] =	[6,4,1+] =	[6,1+,4] =	[1+,6,4,1+] =	[6+,4+]
Generators	{0,1,2}	{010,1,2}	{0,1,212}	{0,101,121,2}	{010,1,212,20102}	{(01)2,(12)2,012}
Orbifold	*642	*443	*662	*3222	*3232	32×
Semidirect subgroups
Diagram
Coxeter		[6,4+]	[6+,4]	[(6,4,2+)]	[6,1+,4,1+] = = = =	[1+,6,1+,4] = = = =
Generators		{0,12}	{01,2}	{02,1,212}	{0,101,(12)2}	{(01)2,121,2}
Orbifold		4*3	6*2	2*32	2*33	3*22
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[6,4]+ =	[6,4+]+ =	[6+,4]+ =	[(6,4,2+)]+ =	[6+,4+]+ = [1+,6,1+,4,1+] = = =
Generators	{01,12}	{(01)2,12}	{01,(12)2}	{02,(01)2,(12)2}	{(01)2,(12)2,201012}
Orbifold	642	443	662	3222	3232
Radical subgroups
Index		8	12	16	24
Diagram
Generators		{0,101,21012,1210121}	{2,121,101020101,0102010, 010101020101010, 10101010201010101}
Coxeter (orbifold)		[6,4*] = (*3333)	[6*,4] (*222222)	[6,4*]+ = (3333)	[6*,4]+ (222222)

Parabolic subgroups

A parabolic subgroup of a Coxeter group can be identified by removing one or more generator mirrors represented with a Coxeter diagram. For example the octahedral group has parabolic subgroups , , , , , . In bracket notation [4,3] has parabolic subgroups [4],[2],[3], and a single mirror []. The order of the subgroup is known, and always an integer divisor group order, or index. Parabolic subgroups can also be written with x nodes, like =[4,3] subgroup by removing second mirror: or = = [4,1^×,3] = [2].

Petrie subgroup

A petrie subgroup of an irreducible coxeter group can be created by the product of all of the generators. It can be seen in the skew regular petrie polygon of a regular polytope. The order of the new group is called the Coxeter number of the original Coxeter group. The Coxeter number of a Coxeter group is 2m/n, where n is the rank, and m is the number of reflections. A petrie subgroup can be written with a π superscript. For example, [3,3]^π is the petrie subgroup of a tetrahedral group, cyclic group order 4, generated by a rotoreflection. A rank 4 Coxeter group will have a double rotation generator, like [4,3,3]^π is order 8.

Extended symmetry

Wallpaper group Triangle symmetry Extended symmetry Extended diagram Extended group Honeycombs p3m1 (*333) a1 [3[3]] ${\displaystyle {\tilde {A}}_{2}}$ (none) p6m (*632) i2 [[3[3]]] ↔ [6,3] ↔ ${\displaystyle {\tilde {A}}_{2}\times 2\leftrightarrow {\tilde {G}}_{2}}$ 1 , 2 p31m (3*3) g3 [3+[3[3]]] ↔ [6,3+] ↔ ${\displaystyle {\tilde {A}}_{2}\times 3\leftrightarrow {\tfrac {1}{2}}{\tilde {G}}_{2}}$ (none) p6 (632) r6 [3[3[3]]]+ ↔ [6,3]+ ↔ ${\displaystyle {\tfrac {1}{2}}{\tilde {A}}_{2}\times 6\leftrightarrow {\tfrac {1}{2}}{\tilde {G}}_{2}}$ (1) p6m (*632) [3[3[3]]] ↔ [6,3] ${\displaystyle {\tilde {A}}_{2}\times 6\leftrightarrow {\tilde {G}}_{2}}$ 3

In the Euclidean plane, the ${\displaystyle {\tilde {A}}_{2}}$, [3[3]] Coxeter group can be extended in two ways into the ${\displaystyle {\tilde {G}}_{2}}$, [6,3] Coxeter group and relates uniform tilings as ringed diagrams.

See also: Goursat tetrahedron § Extended symmetry

Coxeter's notation includes double square bracket notation, [[X]] to express automorphic symmetry within a Coxeter diagram. Johnson added alternative doubling by angled-bracket <[X]>. Johnson also added a prefix symmetry modifier [Y[X]], where Y can either represent symmetry of the Coxeter diagram of [X], or symmetry of the fundamental domain of [X].

For example, in 3D these equivalent rectangle and rhombic geometry diagrams of ${\displaystyle {\tilde {A}}_{3}}$: and , the first doubled with square brackets, [[3^[4]]] or twice doubled as [2[3^[4]]], with [2], order 4 higher symmetry. To differentiate the second, angled brackets are used for doubling, <[3^[4]]> and twice doubled as <2[3^[4]]>, also with a different [2], order 4 symmetry. Finally a full symmetry where all 4 nodes are equivalent can be represented by [4[3^[4]]], with the order 8, [4] symmetry of the square. But by considering the tetragonal disphenoid fundamental domain the [4] extended symmetry of the square graph can be marked more explicitly as [(2⁺,4)[3^[4]]] or [2⁺,4[3^[4]]].

Further symmetry exists in the cyclic ${\displaystyle {\tilde {A}}_{n}}$ and branching ${\displaystyle D_{3}}$, ${\displaystyle {\tilde {E}}_{6}}$, and ${\displaystyle {\tilde {D}}_{4}}$ diagrams. ${\displaystyle {\tilde {A}}_{n}}$ has order 2n symmetry of a regular n-gon, {n}, and is represented by [n[3^[n]]]. ${\displaystyle D_{3}}$ and ${\displaystyle {\tilde {E}}_{6}}$ are represented by [3[3^1,1,1]] = [3,4,3] and [3[3^2,2,2]] respectively while ${\displaystyle {\tilde {D}}_{4}}$ by [(3,3)[3^1,1,1,1]] = [3,3,4,3], with the diagram containing the order 24 symmetry of the regular tetrahedron, {3,3}. The paracompact hyperbolic group ${\displaystyle {\bar {L}}_{5}}$ = [3^1,1,1,1,1], , contains the symmetry of a 5-cell, {3,3,3}, and thus is represented by [(3,3,3)[3^1,1,1,1,1]] = [3,4,3,3,3].

An asterisk * superscript is effectively an inverse operation, creating radical subgroups removing connected of odd-ordered mirrors. ^[7]

Examples:

Example Extended groups and radical subgroups

Extended groups Radical subgroups Coxeter diagrams Index [3[2,2]] = [4,3] [4,3*] = [2,2] = 6 [(3,3)[2,2,2]] = [4,3,3] [4,(3,3)*] = [2,2,2] = 24 [1[31,1]] = [[3,3]] = [3,4] [3,4,1+] = [3,3] = 2 [3[31,1,1]] = [3,4,3] [3*,4,3] = [31,1,1] = 6 [2[31,1,1,1]] = [4,3,3,4] [1+,4,3,3,4,1+] = [31,1,1,1] = 4 [3[3,31,1,1]] = [3,3,4,3] [3*,4,3,3] = [31,1,1,1] = 6 [(3,3)[31,1,1,1]] = [3,4,3,3] [3,4,(3,3)*] = [31,1,1,1] = 24 [2[3,31,1,1,1]] = [3,(3,4)1,1] [3,(3,4,1+)1,1] = [3,31,1,1,1] = 4 [(2,3)[1,131,1,1]] = [4,3,3,4,3] [3*,4,3,3,4,1+] = [31,1,1,1,1] = 12 [(3,3)[3,31,1,1,1]] = [3,3,4,3,3] [3,3,4,(3,3)*] = [31,1,1,1,1] = 24 [(3,3,3)[31,1,1,1,1]] = [3,4,3,3,3] [3,4,(3,3,3)*] = [31,1,1,1,1] = 120

Extended groups Radical subgroups Coxeter diagrams Index [1[3[3]]] = [3,6] [3,6,1+] = [3[3]] = 2 [3[3[3]]] = [6,3] [6,3*] = [3[3]] = 6 [1[3,3[3]]] = [3,3,6] [3,3,6,1+] = [3,3[3]] = 2 [(3,3)[3[3,3]]] = [6,3,3] [6,(3,3)*] = [3[3,3]] = 24 [1[∞]2] = [4,4] [4,1+,4] = [∞]2 = [∞,2,∞] = 2 [2[∞]2] = [4,4] [1+,4,4,1+] = [(4,4,2*)] = [∞]2 = 4 [4[∞]2] = [4,4] [4,4*] = [∞]2 = 8 [2[3[4]]] = [4,3,4] [1+,4,3,4,1+] = [(4,3,4,2*)] = [3[4]] = = 4 [3[∞]3] = [4,3,4] [4,3*,4] = [∞]3 = [∞,2,∞,2,∞] = 6 [(3,3)[∞]3] = [4,31,1] [4,(31,1)*] = [∞]3 = 24 [(4,3)[∞]3] = [4,3,4] [4,(3,4)*] = [∞]3 = 48 [(3,3)[∞]4] = [4,3,3,4] [4,(3,3)*,4] = [∞]4 = 24 [(4,3,3)[∞]4] = [4,3,3,4] [4,(3,3,4)*] = [∞]4 = 384

Looking at generators, the double symmetry is seen as adding a new operator that maps symmetric positions in the Coxeter diagram, making some original generators redundant. For 3D space groups, and 4D point groups, Coxeter defines an index two subgroup of [[X]], [[X]⁺], which he defines as the product of the original generators of [X] by the doubling generator. This looks similar to [[X]]⁺, which is the chiral subgroup of [[X]]. So for example the 3D space groups [[4,3,4]]⁺ (I432, 211) and [[4,3,4]⁺] (Pm3n, 223) are distinct subgroups of [[4,3,4]] (Im3m, 229).

Rank one groups

Further information: One-dimensional symmetry group

In one dimension, the bilateral group [ ] represents a single mirror symmetry, abstract Dih₁ or Z₂, symmetry order 2. It is represented as a Coxeter–Dynkin diagram with a single node, . The identity group is the direct subgroup [ ]⁺, Z₁, symmetry order 1. The + superscript simply implies that alternate mirror reflections are ignored, leaving the identity group in this simplest case. Coxeter used a single open node to represent an alternation, .

Group	Coxeter notation	Coxeter diagram	Order	Description
C1	[ ]+		1	Identity
D2	[ ]		2	Reflection group

Rank two groups

Further information: Point groups in two dimensions

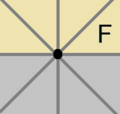
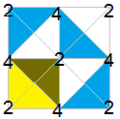
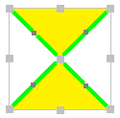
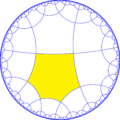
A regular hexagon, with markings on edges and vertices has 8 symmetries: [6], [3], [2], [1], [6] , [3] , [2] , [1] , with [3] and [1] existing in two forms, depending whether the mirrors are on the edges or vertices.

In two dimensions, the rectangular group [2], abstract D₂² or D₄, also can be represented as a direct product [ ]×[ ], being the product of two bilateral groups, represents two orthogonal mirrors, with Coxeter diagram, , with order 4. The 2 in [2] comes from linearization of the orthogonal subgraphs in the Coxeter diagram, as with explicit branch order 2. The rhombic group, [2]⁺ ( or ), half of the rectangular group, the point reflection symmetry, Z₂, order 2.

Coxeter notation to allow a 1 place-holder for lower rank groups, so [1] is the same as [ ], and [1⁺] or [1]⁺ is the same as [ ]⁺ and Coxeter diagram .

The full p-gonal group [p], abstract dihedral group D_2p, (nonabelian for p>2), of order 2p, is generated by two mirrors at angle π/p, represented by Coxeter diagram . The p-gonal subgroup [p]⁺, cyclic group Z_p, of order p, generated by a rotation angle of π/p.

Coxeter notation uses double-bracking to represent an automorphic doubling of symmetry by adding a bisecting mirror to the fundamental domain. For example, [[p]] adds a bisecting mirror to [p], and is isomorphic to [2p].

In the limit, going down to one dimensions, the full apeirogonal group is obtained when the angle goes to zero, so [∞], abstractly the infinite dihedral group D_∞, represents two parallel mirrors and has a Coxeter diagram . The apeirogonal group [∞]⁺, , abstractly the infinite cyclic group Z_∞, isomorphic to the additive group of the integers, is generated by a single nonzero translation.

In the hyperbolic plane, there is a full pseudogonal group [iπ/λ], and pseudogonal subgroup [iπ/λ]⁺, . These groups exist in regular infinite-sided polygons, with edge length λ. The mirrors are all orthogonal to a single line.

Example rank 2 finite and hyperbolic symmetries
Type	Finite					Affine	Hyperbolic
Geometry					...
Coxeter	[ ]	= [2]=[ ]×[ ]	[3]	[4]	[p]	[∞]	[∞]	[iπ/λ]
Order	2	4	6	8	2p	∞
Mirror lines are colored to correspond to Coxeter diagram nodes. Fundamental domains are alternately colored.
Even images (direct)					...
Odd images (inverted)
Coxeter	[ ]+	[2]+	[3]+	[4]+	[p]+	[∞]+	[∞]+	[iπ/λ]+
Order	1	2	3	4	p	∞
Cyclic subgroups represent alternate reflections, all even (direct) images.

Group	Intl	Orbifold	Coxeter	Coxeter diagram	Order	Description
Finite
Zn	n	n•	[n]+		n	Cyclic: n-fold rotations. Abstract group Zn, the group of integers under addition modulo n.
D2n	nm	*n•	[n]		2n	Dihedral: cyclic with reflections. Abstract group Dihn, the dihedral group.
Affine
Z∞	∞	∞•	[∞]+		∞	Cyclic: apeirogonal group . Abstract group Z∞, the group of integers under addition.
Dih∞	∞m	*∞•	[∞]		∞	Dihedral: parallel reflections. Abstract infinite dihedral group Dih∞.
Hyperbolic
Z∞			[πi/λ]+		∞	pseudogonal group
Dih∞			[πi/λ]		∞	full pseudogonal group

Rank three groups

Further information: Point groups in three dimensions and List of spherical symmetry groups

Point groups in 3 dimensions can be expressed in bracket notation related to the rank 3 Coxeter groups:

Finite groups of isometries in 3-space [2]
Rotation groups						Extended groups
Name	Bracket	Orb	Sch	Abstract	Order	Name	Bracket	Orb	Sch	Abstract	Order
Identity	[ ]+	11	C1	Z1	1	Bilateral	[1,1] = [ ]	*	D2	Z2	2
						Central	[2+,2+]	×	Ci	2×Z1	2
Acrorhombic	[1,2]+ = [2]+	22	C2	Z2	2	Acrorectangular	[1,2] = [2]	*22	C2v	D4	4
						Gyrorhombic	[2+,4+]	2×	S4	Z4	4
						Orthorhombic	[2,2+]	2*	D1d	Z2×Z2	4
Pararhombic	[2,2]+	222	D2	D4	4	Gyrorectangular	[2+,4]	2*2	D2d	D8	8
						Orthorectangular	[2,2]	*222	D2h	Z2×D4	8
Acro-p-gonal	[1,p]+ = [p]+	pp	Cp	Zp	p	Full acro-p-gonal	[1,p] = [p]	*pp	Cpv	D2p	2p
						Gyro-p-gonal	[2+,2p+]	p×	S2p	Z2p	2p
						Ortho-p-gonal	[2,p+]	p*	Cph	Z2×Zp	2p
Para-p-gonal	[2,p]+	p22	D2p	D2p	2p	Full gyro-p-gonal	[2+,2p]	2*p	Dpd	D4p	4p
						Full ortho-p-gonal	[2,p]	*p22	Dph	Z2×D2p	4p
Tetrahedral	[3,3]+	332	T	A4	12	Full tetrahedral	[3,3]	*332	Td	S4	24
						Pyritohedral	[3+,4]	3*2	Th	2×A4	24
Octahedral	[3,4]+	432	O	S4	24	Full octahedral	[3,4]	*432	Oh	2×S4	48
Icosahedral	[3,5]+	532	I	A5	60	Full icosahedral	[3,5]	*532	Ih	2×A5	120

In three dimensions, the full orthorhombic group or orthorectangular [2,2], abstractly Z₂³, order 8, represents three orthogonal mirrors, (also represented by Coxeter diagram as three separate dots ). It can also can be represented as a direct product [ ]×[ ]×[ ], but the [2,2] expression allows subgroups to be defined:

First there is a "semidirect" subgroup, the orthorhombic group, [2,2⁺] ( or ), abstractly Z₂×Z₂, of order 4. When the + superscript is given inside of the brackets, it means reflections generated only from the adjacent mirrors (as defined by the Coxeter diagram, ) are alternated. In general, the branch orders neighboring the + node must be even. In this case [2,2⁺] and [2⁺,2] represent two isomorphic subgroups that are geometrically distinct. The other subgroups are the pararhombic group [2,2]⁺ ( or ), also order 4, and finally the central group [2⁺,2⁺] ( or ) of order 2.

Next there is the full ortho-p-gonal group, [2,p] (), abstractly Z₂×D_2p, of order 4p, representing two mirrors at a dihedral angle π/p, and both are orthogonal to a third mirror. It is also represented by Coxeter diagram as .

The direct subgroup is called the para-p-gonal group, [2,p]⁺ ( or ), abstractly D_2p, of order 2p, and another subgroup is [2,p⁺] () abstractly Z₂×Z_p, also of order 2p.

The full gyro-p-gonal group, [2⁺,2p] ( or ), abstractly D_4p, of order 4p. The gyro-p-gonal group, [2⁺,2p⁺] ( or ), abstractly Z_2p, of order 2p is a subgroup of both [2⁺,2p] and [2,2p⁺].

The polyhedral groups are based on the symmetry of platonic solids: the tetrahedron, octahedron, cube, icosahedron, and dodecahedron, with Schläfli symbols {3,3}, {3,4}, {4,3}, {3,5}, and {5,3} respectively. The Coxeter groups for these are: [3,3] (), [3,4] (), [3,5] () called full tetrahedral symmetry, octahedral symmetry, and icosahedral symmetry, with orders of 24, 48, and 120.

Pyritohedral symmetry, [3+,4] is an index 5 subgroup of icosahedral symmetry, [5,3].

In all these symmetries, alternate reflections can be removed producing the rotational tetrahedral [3,3]⁺(), octahedral [3,4]⁺ (), and icosahedral [3,5]⁺ () groups of order 12, 24, and 60. The octahedral group also has a unique index 2 subgroup called the pyritohedral symmetry group, [3⁺,4] ( or ), of order 12, with a mixture of rotational and reflectional symmetry. Pyritohedral symmetry is also an index 5 subgroup of icosahedral symmetry: --> , with virtual mirror 1 across 0, {010}, and 3-fold rotation {12}.

The tetrahedral group, [3,3] (), has a doubling [[3,3]] (which can be represented by colored nodes ), mapping the first and last mirrors onto each other, and this produces the [3,4] ( or ) group. The subgroup [3,4,1⁺] ( or ) is the same as [3,3], and [3⁺,4,1⁺] ( or ) is the same as [3,3]⁺.

Example rank 3 finite Coxeter groups subgroup trees
Tetrahedral symmetry	Octahedral symmetry
Icosahedral symmetry

Finite (point groups in three dimensions)

Intl* Geo [8] Orb. Schön. Struct. Coxeter Ord. 1 1 1 C1 Z1 [] = [ ]+ = 1 2 = m 1 * Cs Z2 [ ] 2 2 3 4 5 6 n 2 3 4 5 6 n 22 33 44 55 66 nn C2 C3 C4 C5 C6 Cn Z2 Z3 Z4 Z5 Z6 Zn [1,2]+ [1,3]+ [1,4]+ [1,5]+ [1,6]+ [1,n]+ 2 3 4 5 6 n 2mm 3m 4mm 5m 6mm nmm nm 2 3 4 5 6 n *22 *33 *44 *55 *66 *nn C2v C3v C4v C5v C6v Cnv D2 D3 D4 D5 D6 Dn [1,2] [1,3] [1,4] [1,5] [1,6] [1,n] 4 6 8 10 12 2n 2/m 3/m 4/m 5/m 6/m n/m 2 2 3 2 4 2 5 2 6 2 n 2 2* 3* 4* 5* 6* n* C2h C3h C4h C5h C6h Cnh Z2×Z2 Z2×Z3 Z2×Z4 Z2×Z5 Z2×Z6 Z2×Zn [2,2+] [2,3+] [2,4+] [2,5+] [2,6+] [2,n+] 4 6 8 10 12 2n 1 4 3 8 5 12 2n n 2 2 4 2 6 2 8 2 10 2 12 2 2n 2 1× 2× 3× 4× 5× 6× n× Ci = S2 S4 S6 S8 S10 S12 S2n Z2 Z4 Z6=Z2×Z3 Z8 Z10=Z2×Z5 Z12 Z2n [2+,2+] [2+,4+] [2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+,2n+] 2 4 6 8 10 12 2n

Intl Geo Orb. Schön. Struct. Coxeter Ord. 222 32 422 52 622 n22 n2 22 32 42 52 62 n2 222 223 224 225 226 22n D2 D3 D4 D5 D6 Dn D4 D6 D8 D10 D12 D2n [2,2]+ [2,3]+ [2,4]+ [2,5]+ [2,6]+ [2,n]+ 4 6 8 10 12 2n mmm 6m2 4/mmm 10m2 6/mmm n/mmm 2nm2 2 2 3 2 4 2 5 2 6 2 n 2 *222 *223 *224 *225 *226 *22n D2h D3h D4h D5h D6h Dnh Z2×D4 Z2×D6 Z2×D8 Z2×D10 Z2×D12 Z2×D2n [2,2] [2,3] [2,4] [2,5] [2,6] [2,n] 8 12 16 20 24 4n 42m 3m 82m 5m 122m 2n2m nm 4 2 6 2 8 2 10 2 12 2 n 2 2*2 2*3 2*4 2*5 2*6 2*n D2d D3d D4d D5d D6d Dnd D4 D6 D8 D10 D12 D2n [2+,4] [2+,6] [2+,8] [2+,10] [2+,12] [2+,2n] 8 12 16 20 24 4n 23 33 332 T A4 [3,3]+ 12 m3 4 3 3*2 Th A4×S2 [3+,4] 24 43m 3 3 *332 Td S4 [3,3] 24 432 43 432 O S4 [3,4]+ 24 m3m 4 3 *432 Oh S4×S2 [3,4] 48 532 53 532 I A5 [3,5]+ 60 53m 5 3 *532 Ih A4×S2 [3,5] 120

Affine

Further information: List of planar symmetry groups

In the Euclidean plane there's 3 fundamental reflective groups generated by 3 mirrors, represented by Coxeter diagrams , , and , and are given Coxeter notation as [4,4], [6,3], and [(3,3,3)]. The parentheses of the last group imply the diagram cycle, and also has a shorthand notation [3^[3]].

[[4,4]] as a doubling of the [4,4] group produced the same symmetry rotated π/4 from the original set of mirrors.

Direct subgroups of rotational symmetry are: [4,4]⁺, [6,3]⁺, and [(3,3,3)]⁺. [4⁺,4] and [6,3⁺] are semidirect subgroups.

Semiaffine (frieze groups) IUC Orb. Geo Sch. Coxeter p1 ∞∞ p1 C∞ [∞] = [∞,1]+ = [∞+,2,1+] = p1m1 *∞∞ p1 C∞v [∞] = [∞,1] = [∞,2,1+] = p11g ∞× p.g1 S2∞ [∞+,2+] p11m ∞* p. 1 C∞h [∞+,2] p2 22∞ p2 D∞ [∞,2]+ p2mg 2*∞ p2g D∞d [∞,2+] p2mm *22∞ p2 D∞h [∞,2]

Affine (Wallpaper groups) IUC Orb. Geo. Coxeter p2 2222 p2 [4,1+,4]+ p2gg 22× pg2g [4+,4+] p2mm *2222 p2 [4,1+,4] c2mm 2*22 c2 [[4+,4+]] p4 442 p4 [4,4]+ p4gm 4*2 pg4 [4+,4] p4mm *442 p4 [4,4] p3 333 p3 [1+,6,3+] = [3[3]]+ = p3m1 *333 p3 [1+,6,3] = [3[3]] = p31m 3*3 h3 [6,3+] = [3[3[3]]+] p6 632 p6 [6,3]+ = [3[3[3]]]+ p6mm *632 p6 [6,3] = [3[3[3]]]

Given in Coxeter notation (orbifold notation), some low index affine subgroups are:

Reflective group	Reflective subgroup	Mixed subgroup	Rotation subgroup	Improper rotation/ translation	Commutator subgroup
[4,4], (*442)	[1+,4,4], (*442) [4,1+,4], (*2222) [1+,4,4,1+], (*2222)	[4+,4], (4*2) [(4,4,2+)], (2*22) [1+,4,1+,4], (2*22)	[4,4]+, (442) [1+,4,4+], (442) [1+,4,1+4,1+], (2222)	[4+,4+], (22×)	[4+,4+]+, (2222)
[6,3], (*632)	[1+,6,3] = [3[3]], (*333)	[3+,6], (3*3)	[6,3]+, (632) [1+,6,3+], (333)		[1+,6,3+], (333)

Rank four groups

Hasse diagram subgroup relations (partial!)

Point groups

Further information: Point groups in four dimensions

Rank four groups defined the 4-dimensional point groups:

Finite groups
[ ]: Symbol Order [1]+ 1.1 [1] = [ ] 2.1 [2]: Symbol Order [1+,2]+ 1.1 [2]+ 2.1 [2] 4.1 [2,2]: Symbol Order [2+,2+]+ = [(2+,2+,2+)] 1.1 [2+,2+] 2.1 [2,2]+ 4.1 [2+,2] 4.1 [2,2] 8.1 [2,2,2]: Symbol Order [(2+,2+,2+,2+)] = [2+,2+,2+]+ 1.1 [2+,2+,2+] 2.1 [2+,2,2+] 4.1 [(2,2)+,2+] 4 [[2+,2+,2+]] 4 [2,2,2]+ 8 [2+,2,2] 8.1 [(2,2)+,2] 8 [[2+,2,2+]] 8.1 [2,2,2] 16.1 [[2,2,2]]+ 16 [[2,2+,2]] 16 [[2,2,2]] 32	[p]: Symbol Order [p]+ p [p] 2p [p,2]: Symbol Order [p,2]+ 2p [p,2] 4p [2p,2+]: Symbol Order [2p,2+] 4p [2p+,2+] 2p [p,2,2]: Symbol Order [p+,2,2+] 2p [(p,2)+,2+] 2p [p,2,2]+ 4p [p,2,2+] 4p [p+,2,2] 4p [(p,2)+,2] 4p [p,2,2] 8p [2p,2+,2]: Symbol Order [2p+,2+,2+]+ p [2p+,2+,2+] 2p [2p+,2+,2] 4p [2p+,(2,2)+] 4p [2p,(2,2)+] 8p [2p,2+,2] 8p	[p,2,q]: Symbol Order [p+,2,q+] pq [p,2,q]+ 2pq [p+,2,q] 2pq [p,2,q] 4pq [(p,2)+,2q]: Symbol Order [(p,2)+,2q+] 2pq [(p,2)+,2q] 4pq [2p,2,2q]: Symbol Order [2p+,2+,2q+]+= [(2p+,2+,2q+,2+)] pq [2p+,2+,2q+] 2pq [2p,2+,2q+] 4pq [((2p,2)+,(2q,2)+)] 4pq [2p,2+,2q] 8pq [[p,2,p]]: Symbol Order [[p+,2,p+]] 2p2 [[p,2,p]]+ 4p2 [[p,2,p]+] 4p2 [[p,2,p]] 8p2 [[2p,2,2p]]: Symbol Order [[(2p+,2+,2p+,2+)]] 2p2 [[2p+,2+,2p+]] 4p2 [[((2p,2)+,(2p,2)+)]] 8p2 [[2p,2+,2p]] 16p2	[3,3,2]: Symbol Order [(3,3)Δ,2,1+] ≅ [2,2]+ 4 [(3,3)Δ,2] ≅ [2,(2,2)+] 8 [(3,3)⅄,2,1+] ≅ [4,2+] 8 [(3,3)+,2,1+] = [3,3]+ 12.5 [(3,3)⅄,2] ≅ [2,4,2+] 16 [3,3,2,1+] = [3,3] 24 [(3,3)+,2] 24.10 [3,3,2]+ 24.10 [3,3,2] 48.36 [4,3,2]: Symbol Order [1+,4,3+,2,1+] = [3,3]+ 12 [3+,4,2+] 24 [(3,4)+,2+] 24 [1+,4,3+,2] = [(3,3)+,2] 24.10 [3+,4,2,1+] = [3+,4] 24.10 [(4,3)+,2,1+] = [4,3]+ 24.15 [1+,4,3,2,1+] = [3,3] 24 [1+,4,(3,2)+] = [3,3,2]+ 24 [3,4,2+] 48 [4,3+,2] 48.22 [4,(3,2)+] 48 [(4,3)+,2] 48.36 [1+,4,3,2] = [3,3,2] 48.36 [4,3,2,1+] = [4,3] 48.36 [4,3,2]+ 48.36 [4,3,2] 96.5 [5,3,2]: Symbol Order [(5,3)+,2,1+] = [5,3]+ 60.13 [5,3,2,1+] = [5,3] 120.2 [(5,3)+,2] 120.2 [5,3,2]+ 120.2 [5,3,2] 240 (nc)	[31,1,1]: Symbol Order [31,1,1]Δ ≅[[4,2+,4]]+ 32 [31,1,1]⅄ 64 [31,1,1]+ 96.1 [31,1,1] 192.2 <[3,31,1]> = [4,3,3] 384.1 [3[31,1,1]] = [3,4,3] 1152.1 [3,3,3]: Symbol Order [3,3,3]+ 60.13 [3,3,3] 120.1 [[3,3,3]]+ 120.2 [[3,3,3]+] 120.1 [[3,3,3]] 240.1 [4,3,3]: Symbol Order [1+,4,(3,3)Δ] = [31,1,1]Δ ≅[[4,2+,4]]+ 32 [4,(3,3)Δ] = [2+,4[2,2,2]+] ≅[[4,2+,4]] 64 [1+,4,(3,3)⅄] = [31,1,1]⅄ 64 [1+,4,(3,3)+] = [31,1,1]+ 96.1 [4,(3,3)⅄] ≅ [[4,2,4]] 128 [1+,4,3,3] = [31,1,1] 192.2 [4,(3,3)+] 192.1 [4,3,3]+ 192.3 [4,3,3] 384.1 [3,4,3]: Symbol Order [3+,4,3+] 288.1 [3,4,3⅄] = [4,3,3] 384.1 [3,4,3]+ 576.2 [3+,4,3] 576.1 [[3+,4,3+]] 576 (nc) [3,4,3] 1152.1 [[3,4,3]]+ 1152 (nc) [[3,4,3]+] 1152 (nc) [[3,4,3]] 2304 (nc) [5,3,3]: Symbol Order [5,3,3]+ 7200 (nc) [5,3,3] 14400 (nc)

Subgroups

1D-4D reflective point groups and subgroups
Order	Reflection		Semidirect subgroups				Direct subgroups		Commutator subgroup
2	[ ]						[ ]+		[ ]+1	[ ]+
4	[2]						[2]+		[2]+2
8	[2,2]		[2+,2]		[2+,2+]		[2,2]+		[2,2]+3
16	[2,2,2]		[2+,2,2] [(2,2)+,2]		[2+,2+,2] [(2,2)+,2+] [2+,2+,2+]		[2,2,2]+ [2+,2,2+]		[2,2,2]+4
	[21,1,1]				[(2+)1,1,1]
2n	[n]						[n]+		[n]+1	[n]+
4n	[2n]						[2n]+		[2n]+2
4n	[2,n]		[2,n+]				[2,n]+		[2,n]+2
8n	[2,2n]		[2+,2n]		[2+,2n+]		[2,2n]+		[2,2n]+3
8n	[2,2,n]		[2+,2,n] [2,2,n+]		[2+,(2,n)+]		[2,2,n]+ [2+,2,n+]		[2,2,n]+3
16n	[2,2,2n]		[2,2+,2n]		[2+,2+,2n] [2,2+,2n+] [(2,2)+,2n+] [2+,2+,2n+]		[2,2,2n]+ [2+,2n,2+]		[2,2,2n]+4
	[2,2n,2]				[2+,2n+,2+]
	[2n,21,1]				[2n+,(2+)1,1]
24	[3,3]						[3,3]+		[3,3]+1	[3,3]+
48	[3,3,2]		[(3,3)+,2]				[3,3,2]+		[3,3,2]+2
48	[4,3]		[4,3+]				[4,3]+		[4,3]+2
96	[4,3,2]		[(4,3)+,2] [4,(3,2)+]				[4,3,2]+		[4,3,2]+3
	[3,4,2]		[3,4,2+] [3+,4,2]		[(3,4)+,2+]		[3+,4,2+]
120	[5,3]						[5,3]+		[5,3]+1	[5,3]+
240	[5,3,2]		[(5,3)+,2]				[5,3,2]+		[5,3,2]+2
4pq	[p,2,q]		[p+,2,q]				[p,2,q]+ [p+,2,q+]		[p,2,q]+2	[p+,2,q+]
8pq	[2p,2,q]		[2p,(2,q)+]		[2p+,(2,q)+]		[2p,2,q]+		[2p,2,q]+3
16pq	[2p,2,2q]		[2p,2+,2q]		[2p+,2+,2q] [2p+,2+,2q+] [(2p,(2,2q)+,2+)]	-	[2p,2,2q]+		[2p,2,2q]+4
120	[3,3,3]						[3,3,3]+		[3,3,3]+1	[3,3,3]+
192	[31,1,1]						[31,1,1]+		[31,1,1]+1	[31,1,1]+
384	[4,3,3]		[4,(3,3)+]				[4,3,3]+		[4,3,3]+2
1152	[3,4,3]		[3+,4,3]				[3,4,3]+ [3+,4,3+]		[3,4,3]+2	[3+,4,3+]
14400	[5,3,3]						[5,3,3]+		[5,3,3]+1	[5,3,3]+

Space groups

Space groups
Affine isomorphism and correspondences	8 cubic space groups as extended symmetry from [3[4]], with square Coxeter diagrams and reflective fundamental domains	35 cubic space groups in International, Fibrifold notation, and Coxeter notation

Rank four groups as 3-dimensional space groups
Triclinic (1-2) Coxeter Space group [∞+,2,∞+,2,∞+] (1) P1 Monoclinic (3-15) Coxeter Space group [(∞,2,∞)+,2,∞+] (3) P2 [∞+,2,∞+,2,∞] (6) Pm [(∞,2,∞)+,2,∞] (10) P2/m Orthorhombic (16-74) Coxeter Space group [∞,2,∞,2,∞]+ (16) P222 [[∞,2,∞,2,∞]]+ (23) I222 [∞+,2,∞,2,∞] (25) Pmm2 [∞,2,∞,2,∞] (47) Pmmm [[∞,2,∞,2,∞]] (71) Immm [∞+,2,∞+,2,∞+] [∞,2,∞,2+,∞] [∞,2+,∞,2+,∞]	Tetragonal (75-142) Coxeter Space group [(4,4)+,2,∞+] (75) P4 [2+[(4,4)+,2,∞+]] (79) I4 [(4,4)+,2,∞] (83) P4/m [2+[(4,4)+,2,∞]] (87) I4/m [4,4,2,∞]+ (89) P422 [2+[4,4,2,∞]]+ (97) I422 [4,4,2,∞+] (99) P4mm [4,4,2,∞] (123) P4/mmm [2+[4,4,2,∞]] (139) I4/mmm [4,(4,2)+,∞] (140) I4/mcm [4,4,2+,∞] [(4,4)+,2+,∞] [4,4,2+,∞+] [(4,4)+,2+,∞+] [4+,4+,2+,∞] [4,4+,2,∞] [4,4+,2+,∞] [((4,2+,4)),2,∞] [4,4+,2,∞+] [4,4+,2+,∞+] [((4,2+,4)),2,∞+]	Trigonal (143-167), rhombohedral Coxeter Space group Hexagonal (168-194) [(6,3)+,2,∞+] (168) P6 [(6,3)+,2,∞] (175) P6/m [6,3,2,∞]+ (177) P622 [6,3,2,∞+] (183) P6mm [6,3,2,∞] (191) P6/mmm [(3[3])+,2,∞+] [3[3],2,∞] [6,3+,2,∞] [6,3+,2,∞+] [3[3],2,∞]+ [3[3],2,∞+] [(3[3])+,2,∞]	Cubic (195-230) Group Coxeter Space group Index [[4,3,4]] [[4,3,4]] (229) Im3m 1 [[4,3,4]]+ (211) I432 2 [[4,3,4]+] (223) Pm3n 2 [[4,3+,4]] (204) I3 2 [[(4,3,4,2+)]] (217) I43m 2 [[4,3+,4]]+ (197) I23 4 [[4,3,4]+]+ (208) P4232 4 [[4,3+,4)]+] (201) Pn43 4 [[(4,3,4,2+)]+] (218) P43n 4 [4,3,4] [4,3,4] (221) Pm3m 2 [4,3,4]+ (207) P432 4 [4,3+,4] (200) Pm3 4 [4,(3,4)+] (226) Fm3c 4 [(4,3,4,2+)] (215) P43m 4 [[{4,(3}+,4)+]] (228) Fd3c 4 [4,3+,4]+ (195) P23 8 [{4,(3}+,4)+] (219) F43c 8 [4,31,1] [4,31,1] (225) Fm3m 4 [4,(31,1)+] (202) Fm3 8 [4,31,1]+ (209) F432 8 [[3[4]]] [(4+,2+)[3[4]]] (222) Pn3n 2 [[3[4]]] (227) Fd3m 4 [[3[4]]]+ (203) Fd3 8 [[3[4]]+] (210) F4132 8 [3[4]] [3[4]] (216) F43m 8 [3[4]]+ (196) F23 16

Line groups

Rank four groups also defined the 3-dimensional line groups:

Semiaffine (3D) groups
Point group			Line group
Hermann-Mauguin		Schönflies	Hermann-Mauguin		Offset type	Wallpaper			Coxeter [∞h,2,pv]
Even n	Odd n		Even n	Odd n		IUC	Orbifold	Diagram
n		Cn	Pnq		Helical: q	p1	o		[∞+,2,n+]
2n	n	S2n	P2n	Pn	None	p11g, pg(h)	××		[(∞,2)+,2n+]
n/m	2n	Cnh	Pn/m	P2n	None	p11m, pm(h)	**		[∞+,2,n]
2n/m		C2nh	P2nn/m		Zigzag	c11m, cm(h)	*×		[∞+,2+,2n]
nmm	nm	Cnv	Pnmm	Pnm	None	p1m1, pm(v)	**		[∞,2,n+]
			Pncc	Pnc	Planar reflection	p1g1, pg(v)	××		[∞+,(2,n)+]
2nmm		C2nv	P2nnmc		Zigzag	c1m1, cm(v)	*×		[∞,2+,2n+]
n22	n2	Dn	Pnq22	Pnq2	Helical: q	p2	2222		[∞,2,n]+
2n2m	nm	Dnd	P2n2m	Pnm	None	p2mg, pmg(h)	22*		[(∞,2)+,2n]
			P2n2c	Pnc	Planar reflection	p2gg, pgg	22×		[+(∞,(2),2n)+]
n/mmm	2n2m	Dnh	Pn/mmm	P2n2m	None	p2mm, pmm	*2222		[∞,2,n]
			Pn/mcc	P2n2c	Planar reflection	p2mg, pmg(v)	22*		[∞,(2,n)+]
2n/mmm		D2nh	P2nn/mcm		Zigzag	c2mm, cmm	2*22		[∞,2+,2n]

Duoprismatic group

Extended duoprismatic symmetry
Extended duoprismatic groups, [p]×[p] or [p,2,p] or , expressed in relation to its tetragonal disphenoid fundamental domain symmetry.

Rank four groups defined the 4-dimensional duoprismatic groups. In the limit as p and q go to infinity, they degenerate into 2 dimensions and the wallpaper groups.

Duoprismatic groups (4D)
Wallpaper			Coxeter [p,2,q]	Coxeter [[p,2,p]]	Wallpaper
IUC	Orbifold	Diagram			IUC	Orbifold	Diagram
p1	o		[p+,2,q+]	[[p+,2,p+]]	p1	o
pg	××		[(p,2)+,2q+]	-
pm	**		[p+,2,q]	-
cm	*×		[2p+,2+,2q]	-
p2	2222		[p,2,q]+	[[p,2,p]]+	p4	442
pmg	22*		[(p,2)+,2q]	-
pgg	22×		[+(2p,(2),2q)+]	[[+(2p,(2),2p)+]]	cmm	2*22
pmm	*2222		[p,2,q]	[[p,2,p]]	p4m	*442
cmm	2*22		[2p,2+,2q]	[[2p,2+,2p]]	p4g	4*2

Wallpaper groups

Rank four groups also defined some of the 2-dimensional wallpaper groups, as limiting cases of the four-dimensional duoprism groups:

Affine (2D plane)
IUC Orb. Geo Coxeter Diagram p1 o p1 [∞+,2,∞+] [∞+,2+,∞+] [(∞+,2+,∞+,2+)] p2 2222 p2 [∞,2,∞]+ [(∞,2+,∞,2+)] p11g ×× pg1 h: [∞+,(2,∞)+] p1g1 v: [(∞,2)+,∞+] p2gm 22* pg2 h: [(∞,2)+,∞] p2mg v: [∞,(2,∞)+]	IUC Orb. Geo Coxeter Diagram p11m ** p1 h: [∞+,2,∞] p1m1 v: [∞,2,∞+] p2mm *2222 p2 [∞,2,∞] c11m *× c1 h: [∞+,2+,∞] c1m1 v: [∞,2+,∞+] p2gg 22× pg2g [+(∞,(2),∞)+] [((∞,2)+)[2]] c2mm 2*22 c2 [∞,2+,∞]

Subgroups of [∞,2,∞], (*2222) can be expressed down to its index 16 commutator subgroup:

Subgroups of [∞,2,∞]
Reflective group	Reflective subgroup	Mixed subgroup	Rotation subgroup	Improper rotation/ translation	Commutator subgroup
[∞,2,∞], (*2222)	[1+,∞,2,∞], (*2222)	[∞+,2,∞], (**)	[∞,2,∞]+, (2222)	[∞,2+,∞]+, (°) [∞+,2+,∞+], (°) [∞+,2,∞+], (°) [∞+,2+,∞], (*×) [(∞,2)+,∞+], (××) [((∞,2)+,(∞,2)+)], (22×)	[(∞+,2+,∞+,2+)], (°)
		[∞,2+,∞], (2*22) [(∞,2)+,∞], (22*)

Complex reflections

Hasse diagram with all subgroup relations on rank 2 Shephard groups.

Coxeter notation has been extended to Complex space, Cⁿ where nodes are unitary reflections of period 2 or greater. Nodes are labeled by an index, assumed to be 2 for ordinary real reflection if suppressed. Complex reflection groups are called Shephard groups rather than Coxeter groups, and can be used to construct complex polytopes.

In ${\displaystyle \mathbb {C} ^{1}}$, a rank 1 Shephard group , order p, is represented as _p[ ], [ ]_p or ]_p[. It has a single generator, representing a 2π/p radian rotation in the Complex plane: ${\displaystyle e^{2\pi i/p}}$.

Coxeter writes the rank 2 complex group, _p[q]_r represents Coxeter diagram . The p and r should only be suppressed if both are 2, which is the real case [q]. The order of a rank 2 group _p[q]_r is ${\displaystyle g=8/q(1/p+2/q+1/r-1)^{-2}}$. ^[9]

The rank 2 solutions that generate complex polygons are: _p[4]₂ (p is 2,3,4,...), ₃[3]₃, ₃[6]₂, ₃[4]₃, ₄[3]₄, ₃[8]₂, ₄[6]₂, ₄[4]₃, ₃[5]₃, ₅[3]₅, ₃[10]₂, ₅[6]₂, and ₅[4]₃ with Coxeter diagrams , , , , , , , , , , , , .

Some subgroup relations among infinite Shephard groups

Infinite groups are ₃[12]₂, ₄[8]₂, ₆[6]₂, ₃[6]₃, ₆[4]₃, ₄[4]₄, and ₆[3]₆ or , , , , , , .

Index 2 subgroups exists by removing a real reflection: _p[2q]₂ → _p[q]_p. Also index r subgroups exist for 4 branches: _p[4]_r → _p[r]_p.

For the infinite family _p[4]₂, for any p = 2, 3, 4,..., there are two subgroups: _p[4]₂ → [p], index p, while and _p[4]₂ → _p[ ]×_p[ ], index 2.

Computation with reflection matrices as symmetry generators

A Coxeter group, represented by Coxeter diagram , is given Coxeter notation [p,q] for the branch orders. Each node in the Coxeter diagram represents a mirror, by convention called ρ_i (and matrix R_i). The generators of this group [p,q] are reflections: ρ₀, ρ₁, and ρ₂. Rotational subsymmetry is given as products of reflections: By convention, σ_0,1 (and matrix S_0,1) = ρ₀ρ₁ represents a rotation of angle π/p, and σ_1,2 = ρ₁ρ₂ is a rotation of angle π/q, and σ_0,2 = ρ₀ρ₂ represents a rotation of angle π/2.

[p,q]⁺, , is an index 2 subgroup represented by two rotation generators, each a products of two reflections: σ_0,1, σ_1,2, and representing rotations of π/p, and π/q angles respectively.

With one even branch, [p⁺,2q], or , is another subgroup of index 2, represented by rotation generator σ_0,1, and reflectional ρ₂.

With even branches, [2p⁺,2q⁺], , is a subgroup of index 4 with two generators, constructed as a product of all three reflection matrices: By convention as: ψ_0,1,2 and ψ_1,2,0, which are rotary reflections, representing a reflection and rotation or reflection.

In the case of affine Coxeter groups like , or , one mirror, usually the last, is translated off the origin. A translation generator τ_0,1 (and matrix T_0,1) is constructed as the product of two (or an even number of) reflections, including the affine reflection. A transreflection (reflection plus a translation) can be the product of an odd number of reflections φ_0,1,2 (and matrix V_0,1,2), like the index 4 subgroup : [4⁺,4⁺] = .

Another composite generator, by convention as ζ (and matrix Z), represents the inversion, mapping a point to its inverse. For [4,3] and [5,3], ζ = (ρ₀ρ₁ρ₂)^h/2, where h is 6 and 10 respectively, the Coxeter number for each family. For 3D Coxeter group [p,q] (), this subgroup is a rotary reflection [2⁺,h⁺].

Coxeter groups are categorized by their rank, being the number of nodes in its Coxeter-Dynkin diagram. The structure of the groups are also given with their abstract group types: In this article, the abstract dihedral groups are represented as Dih_n, and cyclic groups are represented by Z_n, with Dih₁=Z₂.

Rank 2

Dihedral groups	Cyclic groups
[2]	[2]+
[3]	[3]+
[4]	[4]+
[6]	[6]+

Example, in 2D, the Coxeter group [p] () is represented by two reflection matrices R₀ and R₁, The cyclic symmetry [p]⁺ () is represented by rotation generator of matrix S_0,1.

[p], Reflections Rotation Name R0 R1 S0,1=R0×R1 Order 2 2 p Matrix ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&-1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p\\\sin 2\pi /p&-\cos 2\pi /p\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p\\-\sin 2\pi /p&\cos 2\pi /p\\\end{smallmatrix}}\right]}$	[2], Reflections Rotation Name R0 R1 S0,1=R0×R1 Order 2 2 2 Matrix ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&-1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}-1&0\\0&1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}-1&0\\0&-1\\\end{smallmatrix}}\right]}$
[3], Reflections Rotation Name R0 R1 S0,1=R0×R1 Order 2 2 3 Matrix ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&-1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}1/2&{\sqrt {3}}/2\\{\sqrt {3}}/2&-1/2\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}1/2&{\sqrt {3}}/2\\-{\sqrt {3}}/2&1/2\\\end{smallmatrix}}\right]}$	[4], Reflections Rotation Name R0 R1 S0,1=R0×R1 Order 2 2 4 Matrix ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&-1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}0&1\\1&0\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}0&1\\-1&0\\\end{smallmatrix}}\right]}$
[6], Reflections Rotation Name R0 R1 S0,1=R0×R1 Order 2 2 6 Matrix ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&-1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}{\sqrt {3}}/2&1/2\\1/2&-{\sqrt {3}}/2\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}{\sqrt {3}}/2&1/2\\-1/2&{\sqrt {3}}/2\\\end{smallmatrix}}\right]}$	[8], Reflections Rotation Name R0 R1 S0,1=R0×R1 Order 2 2 8 Matrix ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&-1\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2\\{\sqrt {2}}/2&-{\sqrt {2}}/2\\\end{smallmatrix}}\right]}$ ${\displaystyle \left[{\begin{smallmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2\\-{\sqrt {2}}/2&{\sqrt {2}}/2\\\end{smallmatrix}}\right]}$

Rank 3

The finite rank 3 Coxeter groups are [1,p], [2,p], [3,3], [3,4], and [3,5].

To reflect a point through a plane ${\displaystyle ax+by+cz=0}$ (which goes through the origin), one can use ${\displaystyle \mathbf {A} =\mathbf {I} -2\mathbf {NN} ^{T}}$, where ${\displaystyle \mathbf {I} }$ is the 3×3 identity matrix and ${\displaystyle \mathbf {N} }$ is the three-dimensional unit vector for the vector normal of the plane. If the L2 norm of ${\displaystyle a,b,}$ and ${\displaystyle c}$ is unity, the transformation matrix can be expressed as:

${\displaystyle \mathbf {A} =\left[{\begin{smallmatrix}1-2a^{2}&-2ab&-2ac\\-2ab&1-2b^{2}&-2bc\\-2ac&-2bc&1-2c^{2}\end{smallmatrix}}\right]}$

[p,2]

Example fundamental domains, [5,2], as spherical triangles

The reducible 3-dimensional finite reflective group is dihedral symmetry, [p,2], order 4p, . The reflection generators are matrices R₀, R₁, R₂. R₀²=R₁²=R₂²=(R₀×R₁)³=(R₁×R₂)³=(R₀×R₂)²=Identity. [p,2]⁺ () is generated by 2 of 3 rotations: S_0,1, S_1,2, and S_0,2. An order p rotoreflection is generated by V_0,1,2, the product of all 3 reflections.

[p,2],

	Reflections			Rotation			Rotoreflection
Name	R0	R1	R2	S0,1	S1,2	S0,2	V0,1,2
Group
Order	2	2	2	p	2		2p
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p&0\\\sin 2\pi /p&-\cos 2\pi /p&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&1&0\\0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p&0\\-\sin 2\pi /p&\cos 2\pi /p&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p&0\\-\sin 2\pi /p&\cos 2\pi /p&0\\0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}\cos 2\pi /p&-\sin 2\pi /p&0\\-\sin 2\pi /p&-\cos 2\pi /p&0\\0&0&1\\\end{smallmatrix}}\right]}$

[3,3]

reflection lines for [3,3] =

The simplest irreducible 3-dimensional finite reflective group is tetrahedral symmetry, [3,3], order 24, . The reflection generators, from a D₃=A₃ construction, are matrices R₀, R₁, R₂. R₀²=R₁²=R₂²=(R₀×R₁)³=(R₁×R₂)³=(R₀×R₂)²=Identity. [3,3]⁺ () is generated by 2 of 3 rotations: S_0,1, S_1,2, and S_0,2. A trionic subgroup, isomorphic to [2⁺,4], order 8, is generated by S_0,2 and R₁. An order 4 rotoreflection is generated by V_0,1,2, the product of all 3 reflections.

[3,3],

	Reflections			Rotations			Rotoreflection
Name	R0	R1	R2	S0,1	S1,2	S0,2	V0,1,2
Name
Order	2	2	2	3		2	4
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&0&1\\0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&0&-1\\0&-1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\0&0&1\\1&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&0&-1\\1&0&0\\0&-1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&0&-1\\0&-1&0\\1&0&0\\\end{smallmatrix}}\right]}$
	(0,1,−1)n	(1,−1,0)n	(0,1,1)n	(1,1,1)axis	(1,1,−1)axis	(1,0,0)axis

[4,3]

Reflection lines for [4,3] =

Another irreducible 3-dimensional finite reflective group is octahedral symmetry, [4,3], order 48, . The reflection generators matrices are R₀, R₁, R₂. R₀²=R₁²=R₂²=(R₀×R₁)⁴=(R₁×R₂)³=(R₀×R₂)²=Identity. Chiral octahedral symmetry, [4,3]⁺, () is generated by 2 of 3 rotations: S_0,1, S_1,2, and S_0,2. Pyritohedral symmetry [4,3⁺], () is generated by reflection R₀ and rotation S_1,2. A 6-fold rotoreflection is generated by V_0,1,2, the product of all 3 reflections.

[4,3],

	Reflections			Rotations			Rotoreflection
Name	R0	R1	R2	S0,1	S1,2	S0,2	V0,1,2
Group
Order	2	2	2	4	3	2	6
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&1&0\\0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&0&1\\0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&0&1\\0&-1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\0&0&1\\1&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\0&0&1\\-1&0&0\\\end{smallmatrix}}\right]}$
	(0,0,1)n	(0,1,−1)n	(1,−1,0)n	(1,0,0)axis	(1,1,1)axis	(1,−1,0)axis

[5,3]

Reflection lines for [5,3] =

A final irreducible 3-dimensional finite reflective group is icosahedral symmetry, [5,3], order 120, . The reflection generators matrices are R₀, R₁, R₂. R₀²=R₁²=R₂²=(R₀×R₁)⁵=(R₁×R₂)³=(R₀×R₂)²=Identity. [5,3]⁺ () is generated by 2 of 3 rotations: S_0,1, S_1,2, and S_0,2. A 10-fold rotoreflection is generated by V_0,1,2, the product of all 3 reflections.

[5,3],

	Reflections			Rotations			Rotoreflection
Name	R0	R1	R2	S0,1	S1,2	S0,2	V0,1,2
Group
Order	2	2	2	5	3	2	10
Matrix	${\displaystyle \left[{\begin{smallmatrix}-1&0&0\\0&1&0\\0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}{\frac {1-\phi }{2}}&{\frac {-\phi }{2}}&{\frac {-1}{2}}\\{\frac {-\phi }{2}}&{\frac {1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {1-\phi }{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}{\frac {\phi -1}{2}}&{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {-\phi }{2}}&{\frac {1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {1-\phi }{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}{\frac {1-\phi }{2}}&{\frac {\phi }{2}}&{\frac {-1}{2}}\\{\frac {-\phi }{2}}&{\frac {-1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {\phi -1}{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&0\\0&-1&0\\0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}{\frac {\phi -1}{2}}&{\frac {-\phi }{2}}&{\frac {1}{2}}\\{\frac {-\phi }{2}}&{\frac {-1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {\phi -1}{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}$
	(1,0,0)n	(φ,1,φ−1)n	(0,1,0)n	(φ,1,0)axis	(1,1,1)axis	(1,0,0)axis

Rank 4

Further information: Point groups in four dimensions

There are 4 irreducible Coxeter groups in 4 dimensions: [3,3,3], [4,3,3], [3^1,1,1], [3,4,4], [5,3,3], as well as an infinite family of duoprismatic groups [p,2,q].

[p,2,q]

The duprismatic group, [p,2,q], has order 4pq.

[p,2,q],

	Reflections
Name	R0	R1	R2	R3
Group element
Order	2	2	2	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&-1&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p&0&0\\\sin 2\pi /p&-\cos 2\pi /p&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&\cos 2\pi /q&\sin 2\pi /q\\0&0&\sin 2\pi /q&-\cos 2\pi /q\\\end{smallmatrix}}\right]}$

[[p,2,p]]

The duoprismatic group can double in order, to 8p², with a 2-fold rotation between the two planes.

[[p,2,p]],

	Rotation	Reflections
Name	T	R0	R1	R2=TR1T	R3=TR0T
Element
Order	2	2	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&-1&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p&0&0\\\sin 2\pi /p&-\cos 2\pi /p&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&0&0&-1\\0&0&-1&0\\0&-1&0&0\\-1&0&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&\cos 2\pi /p&\sin 2\pi /p\\0&0&\sin 2\pi /p&-\cos 2\pi /p\\\end{smallmatrix}}\right]}$

[3,3,3]

Hypertetrahedral symmetry, [3,3,3], order 120, is easiest to represent with 4 mirrors in 5-dimensions, as a subgroup of [4,3,3,3].

[3,3,3],

	Reflections				Rotations						Rotoreflections		Double rotation
Name	R0	R1	R2	R3	S0,1	S1,2	S2,3	S0,2	S1,3	S2,3	V0,1,2	V0,1,3	W0,1,2,3
Element group
Order	2	2	2	2	3			2			4	6	5
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&0&1\\0&0&0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&1&0&0&0\\0&0&0&1&0\\0&0&1&0&0\\0&0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&0&1&0&0\\0&1&0&0&0\\0&0&0&1&0\\0&0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0&0\\1&0&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&1&0&0&0\\0&0&0&1&0\\0&0&0&0&1\\0&0&1&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&1&0&0&0\\0&0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&1&0&0&0\\0&0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&0&1&0&0\\0&1&0&0&0\\0&0&0&0&1\\0&0&0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0&0\\1&0&0&0&0\\0&0&0&1&0\\0&0&1&0&0\\0&0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0&0\\1&0&0&0&0\\0&0&1&0&0\\0&0&0&0&1\\0&0&0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\\0&1&0&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0&0\\1&0&0&0&0\\0&0&0&1&0\\0&0&0&0&1\\0&0&1&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\\1&0&0&0&0\\\end{smallmatrix}}\right]}$
	(0,0,0,1,-1)n	(0,0,1,−1,0)n	(0,1,−1,0,0)n	(1,−1,0,0,0)n

[[3,3,3]]

The extended group [[3,3,3]], order 240, is doubled by a 2-fold rotation matrix T, here reversing coordinate order and sign: There are 3 generators {T, R₀, R₁}. Since T is self-reciprocal R₃=TR₀T, and R₂=TR₁T.

[[3,3,3]],

	Rotation	Reflections
Name	T	R0	R1	TR1T=R2	TR0T=R3
Element group
Order	2	2	2	2	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}0&0&0&0&-1\\0&0&0&-1&0\\0&0&-1&0&0\\0&-1&0&0&0\\-1&0&0&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&0&1\\0&0&0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&1&0&0&0\\0&0&0&1&0\\0&0&1&0&0\\0&0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0\\0&0&1&0&0\\0&1&0&0&0\\0&0&0&1&0\\0&0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0&0\\1&0&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\\\end{smallmatrix}}\right]}$
		(0,0,0,1,-1)n	(0,0,1,−1,0)n	(0,1,−1,0,0)n	(1,−1,0,0,0)n

[4,3,3]

A irreducible 4-dimensional finite reflective group is hyperoctahedral group (or hexadecachoric group (for 16-cell), B₄=[4,3,3], order 384, . The reflection generators matrices are R₀, R₁, R₂, R₃. R₀²=R₁²=R₂²=R₃²=(R₀×R₁)⁴=(R₁×R₂)³=(R₂×R₃)³=(R₀×R₂)²=(R₁×R₃)²=(R₀×R₃)²=Identity.

Chiral hyperoctahedral symmetry, [4,3,3]⁺, () is generated by 3 of 6 rotations: S_0,1, S_1,2, S_2,3, S_0,2, S_1,3, and S_0,3. Hyperpyritohedral symmetry [4,(3,3)⁺], () is generated by reflection R₀ and rotations S_1,2 and S_2,3. An 8-fold double rotation is generated by W_0,1,2,3, the product of all 4 reflections.

[4,3,3],

	Reflections				Rotations						Rotoreflection				Double rotation
Name	R0	R1	R2	R3	S0,1	S1,2	S2,3	S0,2	S1,3	S0,3	V1,2,3	V0,1,3	V0,1,2	V0,2,3	W0,1,2,3
Group
Order	2	2	2	2	4	3		2			4		6		8
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&-1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&0&0&1\\0&1&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\1&0&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\1&0&0&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&-1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&0&0&1\\0&0&-1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\1&0&0&0\\0&0&0&-1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\-1&0&0&0\\\end{smallmatrix}}\right]}$
	(0,0,0,1)n	(0,0,1,−1)n	(0,1,−1,0)n	(1,−1,0,0)n

[3,3^1,1]

A half group of [4,3,3] is [3,3^1,1], , order 192. It shares 3 generators with [4,3,3] group, but has two copies of an adjacent generator, one reflected across the removed mirror.

[3,3^1,1],

	Reflections
Name	R0	R1	R2	R3
Group
Order	2	2	2	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&0&-1\\0&0&-1&0\\\end{smallmatrix}}\right]}$
	(1,−1,0,0)n	(0,1,−1,0)n	(0,0,1,−1)n	(0,0,1,1)n

[3,4,3]

A irreducible 4-dimensional finite reflective group is Icositetrachoric group (for 24-cell), F₄=[3,4,3], order 1152, . The reflection generators matrices are R₀, R₁, R₂, R₃. R₀²=R₁²=R₂²=R₃²=(R₀×R₁)³=(R₁×R₂)⁴=(R₂×R₃)³=(R₀×R₂)²=(R₁×R₃)²=(R₀×R₃)²=Identity.

Chiral icositetrachoric symmetry, [3,4,3]⁺, () is generated by 3 of 6 rotations: S_0,1, S_1,2, S_2,3, S_0,2, S_1,3, and S_0,3. Ionic diminished [3,4,3⁺] group, () is generated by reflection R₀ and rotations S_1,2 and S_2,3. A 12-fold double rotation is generated by W_0,1,2,3, the product of all 4 reflections.

[3,4,3],

	Reflections				Rotations
Name	R0	R1	R2	R3	S0,1	S1,2	S2,3	S0,2	S1,3	S0,3
Element group
Order	2	2	2	2	3	4	3	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1/2&-1/2&-1/2&-1/2\\-1/2&1/2&-1/2&-1/2\\-1/2&-1/2&1/2&-1/2\\-1/2&-1/2&-1/2&1/2\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\1&0&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&-1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1/2&-1/2&1/2&-1/2\\-1/2&1/2&1/2&-1/2\\-1/2&-1/2&-1/2&-1/2\\-1/2&-1/2&1/2&1/2\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1/2&-1/2&-1/2&-1/2\\-1/2&-1/2&1/2&-1/2\\-1/2&1/2&-1/2&-1/2\\-1/2&-1/2&-1/2&1/2\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&1/2&-1/2&-1/2\\1/2&-1/2&-1/2&-1/2\\-1/2&-1/2&1/2&-1/2\\-1/2&1/2&-1/2&1/2\\\end{smallmatrix}}\right]}$
	(1,−1,0,0)n	(0,1,−1,0)n	(0,0,1,0)n	(−1,−1,−1,−1)n

[3,4,3],

	Rotoreflection				Double rotation
Name	V1,2,3	V0,1,3	V0,1,2	V0,2,3	W0,1,2,3
Element group
Order	6				12
Matrix	${\displaystyle \left[{\begin{smallmatrix}-1/2&1/2&-1/2&-1/2\\-1/2&-1/2&1/2&-1/2\\1/2&-1/2&-1/2&-1/2\\-1/2&-1/2&-1/2&1/2\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\-1&0&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1/2&1/2&-1/2&-1/2\\-1/2&1/2&1/2&-1/2\\-1/2&-1/2&-1/2&-1/2\\-1/2&1/2&-1/2&1/2\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&1/2&1/2&-1/2\\1/2&-1/2&1/2&-1/2\\-1/2&-1/2&-1/2&-1/2\\-1/2&-1/2&1/2&1/2\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1/2&1/2&-1/2&-1/2\\1/2&-1/2&1/2&-1/2\\-1/2&-1/2&-1/2&-1/2\\1/2&-1/2&-1/2&1/2\\\end{smallmatrix}}\right]}$

[[3,4,3]]

The group [[3,4,3]] extends [3,4,3] by a 2-fold rotation, T, doubling order to 2304.

[[3,4,3]],

	Rotation	Reflections
Name	T	R0	R1	R2 = TR1T	R3 = TR0T
Element group
Order	2	2	2	2	2
Matrix		${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1/2&-1/2&-1/2&-1/2\\-1/2&1/2&-1/2&-1/2\\-1/2&-1/2&1/2&-1/2\\-1/2&-1/2&-1/2&1/2\\\end{smallmatrix}}\right]}$
		(1,−1,0,0)n	(0,1,−1,0)n	(0,0,1,0)n	(−1,−1,−1,−1)n

[5,3,3]

Stereographic projections

[5,3,3]+ 72 order-5 gyrations	[5,3,3]+ 200 order-3 gyrations
[5,3,3]+ 450 order-2 gyrations	[5,3,3]+ all gyrations

The hyper-icosahedral symmetry, [5,3,3], order 14400, . The reflection generators matrices are R₀, R₁, R₂, R₃. R₀²=R₁²=R₂²=R₃²=(R₀×R₁)⁵=(R₁×R₂)³=(R₂×R₃)³=(R₀×R₂)²=(R₀×R₃)²=(R₁×R₃)²=Identity. [5,3,3]⁺ () is generated by 3 rotations: S_0,1 = R₀×R₁, S_1,2 = R₁×R₂, S_2,3 = R₂×R₃, etc.

[5,3,3],

	Reflections
Name	R0	R1	R2	R3
Element group
Order	2	2	2	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}{\frac {1-\phi }{2}}&{\frac {-\phi }{2}}&{\frac {-1}{2}}&0\\{\frac {-\phi }{2}}&{\frac {1}{2}}&{\frac {1-\phi }{2}}&0\\{\frac {-1}{2}}&{\frac {1-\phi }{2}}&{\frac {\phi }{2}}&0\\0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&-1&0&0\\0&0&1&0\\0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&{\frac {1}{2}}&{\frac {\phi }{2}}&{\frac {1-\phi }{2}}\\0&{\frac {\phi }{2}}&{\frac {1-\phi }{2}}&{\frac {1}{2}}\\0&{\frac {1-\phi }{2}}&{\frac {1}{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}$
	(1,0,0,0)n	(φ,1,φ−1,0)n	(0,1,0,0)n	(0,−1,φ,1−φ)n

Rank 8

[3^4,2,1]

The E8 Coxeter group, [3^4,2,1], , has 8 mirror nodes, order 696729600 (192x10!). E7 and E6, [3^3,2,1], , and [3^2,2,1], can be constructed by ignoring the first mirror or the first two mirrors respectively.

E8=[3^4,2,1],

	Reflections
Name	R0	R1	R2	R3	R4	R5	R6	R7
Element group
Order	2	2	2	2	2	2	2	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0&0&0&0&0\\1&0&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&0&-1&0\\0&0&0&0&0&-1&0&0\\0&0&0&0&0&0&0&1\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}3/4&-1/4&-1/4&-1/4&-1/4&-1/4&-1/4&-1/4\\-1/4&3/4&-1/4&-1/4&-1/4&-1/4&-1/4&-1/4\\-1/4&-1/4&3/4&-1/4&-1/4&-1/4&-1/4&-1/4\\-1/4&-1/4&-1/4&3/4&-1/4&-1/4&-1/4&-1/4\\-1/4&-1/4&-1/4&-1/4&3/4&-1/4&-1/4&-1/4\\-1/4&-1/4&-1/4&-1/4&-1/4&3/4&-1/4&-1/4\\-1/4&-1/4&-1/4&-1/4&-1/4&-1/4&3/4&-1/4\\-1/4&-1/4&-1/4&-1/4&-1/4&-1/4&-1/4&3/4\end{smallmatrix}}\right]}$
	(1,-1,0,0,0,0,0,0)n	(0,1,-1,0,0,0,0,0)n	(0,0,1,-1,0,0,0,0)n	(0,0,0,1,-1,0,0,0)n	(0,0,0,0,1,-1,0,0)n	(0,0,0,0,0,1,-1,0)n	(0,0,0,0,0,1,1,0)n	(1,1,1,1,1,1,1,1)n

Affine rank 2

Affine matrices are represented by adding an extra row and column, the last row being zero except last entry 1. The last column represents a translation vector.

[∞]

The affine group [∞], , can be given by two reflection matrices, x=0 and x=1.

[∞],

	Reflections		Translation
Name	R0	R1	S0,1
Element group
Order	2	2	∞
Matrix	${\displaystyle \left[{\begin{smallmatrix}-1&0\\0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&1\\0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&-1\\0&1\\\end{smallmatrix}}\right]}$
Hyperplane	x=0	x=1

Affine rank 3

[4,4]

Further information: Tetrakis_square_tiling § Symmetry

The affine group [4,4], , (p4m), can be given by three reflection matrices, reflections across the x axis (y=0), a diagonal (x=y), and the affine reflection across the line (x=1). [4,4]⁺ () (p4) is generated by S_0,1 S_1,2, and S_0,2. [4⁺,4⁺] () (pgg) is generated by 2-fold rotation S_0,2 and glide reflection (transreflection) V_0,1,2. [4⁺,4] () (p4g) is generated by S_0,1 and R₃. The group [(4,4,2⁺)] () (cmm), is generated by 2-fold rotation S_1,3 and reflection R₂.

[4,4],

	Reflections			Rotations			Glides
Name	R0	R1	R2	S0,1	S1,2	S0,2	V0,1,2	V0,2,1
Element group
Order	2	2	2	4		2	∞ (2)
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&2\\0&1&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\-1&0&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\-1&0&2\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&2\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\1&0&-2\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&-1&2\\-1&0&0\\0&0&1\\\end{smallmatrix}}\right]}$
Hyperplane	y=0	x=y	x=1

[3,6]

The affine group [3,6], , (p6m), can be given by three reflection matrices, reflections across the x axis (y=0), line y=(√3/2)x, and vertical line x=1.

[3,6],

	Reflections			Rotations			Glides
Name	R0	R1	R2	S0,1	S1,2	S0,2	V0,1,2	V0,2,1
Element group
Order	2	2	2	3	6	2	∞ (2)
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&{\sqrt {3}}/2&0\\{\sqrt {3}}/2&1/2&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&2\\0&1&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&{\sqrt {3}}/2&0\\-{\sqrt {3}}/2&-1/2&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1/2&{\sqrt {3}}/2&-1\\-{\sqrt {3}}/2&1/2&{\sqrt {3}}\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&2\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1/2&{\sqrt {3}}/2&-1\\{\sqrt {3}}/2&-1/2&-{\sqrt {3}}\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1/2&-{\sqrt {3}}/2&2\\-{\sqrt {3}}/2&-1/2&0\\0&0&1\\\end{smallmatrix}}\right]}$
Hyperplane	y=0	y=(√3/2)x	x=1

[3^[3]]

The affine group [3^[3]] can be constructed as a half group of . R₂ is replaced by R'₂ = R₂×R₁×R₂, presented by the hyperplane: y+(√3/2)x=2. The fundamental domain is an equilateral triangle with edge length 2.

[3^[3]],

	Reflections			Rotations			Glides
Name	R0	R1	R'2 = R2×R1×R2	S0,1	S1,2	S0,2	V0,1,2	V0,2,1
Element group
Order	2	2	2	3			∞ (2)
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&{\sqrt {3}}/2&0\\{\sqrt {3}}/2&1/2&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&-{\sqrt {3}}/2&3\\-{\sqrt {3}}/2&1/2&{\sqrt {3}}\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0\\-1&0&0\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&{\sqrt {3}}/2&0\\-{\sqrt {3}}/2&-1/2&2{\sqrt {3}}\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&-{\sqrt {3}}/2&3\\{\sqrt {3}}/2&-1/2&-{\sqrt {3}}\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&{\sqrt {3}}/2&0\\{\sqrt {3}}/2&1/2&-2{\sqrt {3}}\\0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1/2&-{\sqrt {3}}/2&3\\-{\sqrt {3}}/2&1/2&-{\sqrt {3}}\\0&0&1\\\end{smallmatrix}}\right]}$
Hyperplane	y=0	y=(√3/2)x	y+(√3/2)x=2

Affine rank 4

[4,3,4]

[4,3,4] fundamental domain

The affine group is [4,3,4] (), can be given by four reflection matrices. Mirror R₀ can be put on z=0 plane. Mirror R₁ can be put on plane y=z. Mirror R₂ can be put on x=y plane. Mirror R₃ can be put on x=1 plane. [4,3,4]⁺ () is generated by S_0,1, S_1,2, and S_2,3.

[4,3,4],

	Reflections				Rotations						Transflections		Screw axis
Name	R0	R1	R2	R3	S0,1	S1,2	S2,3	S0,2	S0,3	S1,3	T0,1,2	T1,2,3	U0,1,2,3
Element group
Order	2	2	2	2	4	3	4	2			6		∞ (3)
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&0&2\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&-1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\1&0&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\-1&0&0&2\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&0&2\\0&1&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&0&2\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\-1&0&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\-1&0&0&2\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\1&0&0&-2\\0&0&0&1\\\end{smallmatrix}}\right]}$
Hyperplane	z=0	y=z	x=y	x=1

[[4,3,4]]

The extended group [[4,3,4]] doubles the group order, adding with a 2-fold rotation matrix T, with a fixed axis through points (1,1/2,0) and (1/2,1/2,1/2). The generators are {R₀,R₁,T}. R₂ = T×R₁×T and R₃ = T×R₀×T.

[[4,3,4]],

	Rotation	Reflections
Name	T	R0	R1	R2 = T×R1×T	R3 = T×R0×T
Element group
Order	2	2	2	2	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}0&0&-1&1\\0&-1&0&1\\-1&0&0&1\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&0&2\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$
Hyperplane	Point (1/2,1/2,1/2) Axis (-1,0,1)	z=0	y=z	x=y	x=1

[4,3^1,1]

[4,3 ] fundamental domain

The group [4,3^1,1] can be constructed from [4,3,4], by computing [4,3,4,1⁺], , as R'₃=R₃×R₂×R₃, with new R'₃ as an image of R₂ across R₃.

[4,3^1,1],

	Reflections				Rotations
Name	R0	R1	R2	R'3	S0,1	S1,2	S1,3	S0,2	S0,3	S2,3
Element group
Order	2	2	2	2	3	3	3	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&-1&0&2\\-1&0&0&2\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&-1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\1&0&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&-1&0&2\\0&0&1&0\\-1&0&0&2\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&-1&0&2\\-1&0&0&2\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&0&2\\0&-1&0&2\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$
Hyperplane	z=0	y=z	x=y	x+y=2

[3^[4]]

[3 ] fundamental domain

The group [3^[4]] can be constructed from [4,3,4], by removing first and last mirrors, [1⁺,4,3,4,1⁺], , by R'₁=R₀×R₁×R₀ and R'₃=R₃×R₂×R₃.

[3^[4]]

	Reflections				Rotations
Name	R'0	R1	R2	R'3	S0,1	S1,2	S1,3	S0,2	S0,3	S2,3
Element group
Order	2	2	2	2	3	3	3	2
Matrix	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&-1&0\\0&-1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&-1&0&2\\-1&0&0&2\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&1&0\\1&0&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&-1&0&2\\0&0&1&0\\-1&0&0&2\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&1&0&0\\0&0&-1&0\\-1&0&0&0\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}0&-1&0&2\\0&0&-1&0\\1&0&0&-2\\0&0&0&1\\\end{smallmatrix}}\right]}$	${\displaystyle \left[{\begin{smallmatrix}-1&0&0&2\\0&-1&0&2\\0&0&1&0\\0&0&0&1\\\end{smallmatrix}}\right]}$
Hyperplane	y=-z	y=z	x=y	x+y=2

Notes

1. Johnson (2018), 11.6 Subgroups and extensions, p 255, halving subgroups
2. Johnson (2018), pp.231-236, and p 245 Table 11.4 Finite groups of isometries in 3-space
3. Johnson (2018), 11.6 Subgroups and extensions, p 259, radical subgroup
4. Johnson (2018), 11.6 Subgroups and extensions, p 258, trionic subgroups
5. Conway, 2003, p.46, Table 4.2 Chiral groups II
6. Coxeter and Moser, 1980, Sec 9.5 Commutator subgroup, p. 124–126
7. Johnson, Norman W.; Weiss, Asia Ivić (1999). "Quaternionic modular groups". Linear Algebra and Its Applications. 295 (1–3): 159–189. doi: 10.1016/S0024-3795(99)00107-X .
8. The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF Archived 2020-10-20 at the Wayback Machine
9. Coxeter, Regular Complex Polytopes, 9.7 Two-generator subgroups reflections. pp. 178–179

References

• H.S.M. Coxeter:
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6
    • (Paper 22) Coxeter, H.S.M. (1940), "Regular and Semi Regular Polytopes I", Math. Z., 46: 380–407, doi:10.1007/bf01181449, S2CID   186237114
    • (Paper 23) Coxeter, H.S.M. (1985), "Regular and Semi-Regular Polytopes II", Math. Z., 188 (4): 559–591, doi:10.1007/bf01161657, S2CID   120429557
    • (Paper 24) Coxeter, H.S.M. (1988), "Regular and Semi-Regular Polytopes III", Math. Z., 200: 3–45, doi:10.1007/bf01161745, S2CID   186237142
• Coxeter, H. S. M.; Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN   0-387-09212-9.
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
  • Norman W. Johnson and Asia Ivic Weiss Quadratic Integers and Coxeter Groups Archived 2023-03-26 at the Wayback Machine PDF Can. J. Math. Vol. 51 (6), 1999 pp. 1307–1336
  • N. W. Johnson: Geometries and Transformations, (2018) ISBN   978-1-107-10340-5 PDF
• Conway, John Horton; Delgado Friedrichs, Olaf; Huson, Daniel H.; Thurston, William P. (2001), "On three-dimensional space groups", Beiträge zur Algebra und Geometrie, 42 (2): 475–507, ISSN   0138-4821, MR   1865535
• John H. Conway and Derek A. Smith, On Quaternions and Octonions, 2003, ISBN   978-1-56881-134-5
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN   978-1-56881-220-5 Ch.22 35 prime space groups, ch.25 184 composite space groups, ch.26 Higher still, 4D point groups