In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).
A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. For each wallpaper there corresponds a group of congruent transformations, with function composition as the group operation. Thus, a wallpaper group is a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations, tiles and physical wallpaper.
In geometry, a glide reflection or transflection is a geometric transformation that consists of a reflection across a hyperplane and a translation ("glide") in a direction parallel to that hyperplane, combined into a single transformation. Because the distances between points are not changed under glide reflection, it is a motion or isometry. When the context is the two-dimensional Euclidean plane, the hyperplane of reflection is a straight line called the glide line or glide axis. When the context is three-dimensional space, the hyperplane of reflection is a plane called the glide plane. The displacement vector of the translation is called the glide vector.
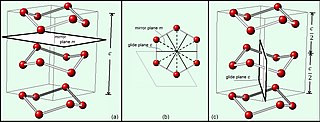
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups.
In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space ; that is, the transformations of that space that preserve the Euclidean distance between any two points (also called Euclidean transformations). The group depends only on the dimension n of the space, and is commonly denoted E(n) or ISO(n).
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.
In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation. Discrete translational symmetry is invariant under discrete translation.
The Schoenfliesnotation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation.
In geometry, a point group is a mathematical group of symmetry operations (isometries in a Euclidean space) that have a fixed point in common. The coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every point group in dimension d is then a subgroup of the orthogonal group O(d). Point groups are used to describe the symmetries of geometric figures and physical objects such as molecules.
In geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length. There are four types: translations, rotations, reflections, and glide reflections.
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.
A regular octahedron has 24 rotational symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedron that is dual to an octahedron.
In geometry, orbifold notation is a system, invented by the mathematician William Thurston and promoted by John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature. The advantage of the notation is that it describes these groups in a way which indicates many of the groups' properties: in particular, it follows William Thurston in describing the orbifold obtained by taking the quotient of Euclidean space by the group under consideration.
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dihn.
In three dimensional geometry, there are four infinite series of point groups in three dimensions (n≥1) with n-fold rotational or reflectional symmetry about one axis (by an angle of 360°/n) that does not change the object.
In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries (isometries) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O(2), including O(2) itself. Its elements are rotations and reflections, and every such group containing only rotations is a subgroup of the special orthogonal group SO(2), including SO(2) itself. That group is isomorphic to R/Z and the first unitary group, U(1), a group also known as the circle group.
In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.
A line group is a mathematical way of describing symmetries associated with moving along a line. These symmetries include repeating along that line, making that line a one-dimensional lattice. However, line groups may have more than one dimension, and they may involve those dimensions in its isometries or symmetry transformations.
In geometry, an object has symmetry if there is an operation or transformation that maps the figure/object onto itself. Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be symmetric under rotation or to have rotational symmetry. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry.
