
In mathematics, a group is a non-empty set and an operation that combines any two elements of the set to produce a third element of the set, in such a way that the operation is associative, an identity element exists and every element has an inverse. These three axioms hold for number systems and many other mathematical structures. For example, the integers together with the addition operation form a group. The concept of a group and the axioms that define it were elaborated for handling, in a unified way, essential structural properties of very different mathematical entities such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics.

In abstract algebra, a branch of mathematics, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being 0.

In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative internal binary operation on it.

In group theory, a branch of mathematics, given a group G under a binary operation ∗, a subset H of G is called a subgroup of G if H also forms a group under the operation ∗. More precisely, H is a subgroup of G if the restriction of ∗ to H × H is a group operation on H. This is often denoted H ≤ G, read as "H is a subgroup of G".
In mathematics, a presentation is one method of specifying a group. A presentation of a group G comprises a set S of generators—so that every element of the group can be written as a product of powers of some of these generators—and a set R of relations among those generators. We then say G has presentation
In mathematics, in particular abstract algebra, a graded ring is a ring such that the underlying additive group is a direct sum of abelian groups such that . The index set is usually the set of nonnegative integers or the set of integers, but can be any monoid. The direct sum decomposition is usually referred to as gradation or grading.

In mathematics, a group G is called the direct sum of two normal subgroups with trivial intersection if it is generated by the subgroups. In abstract algebra, this method of construction of groups can be generalized to direct sums of vector spaces, modules, and other structures; see the article direct sum of modules for more information. A group which can be expressed as a direct sum of non-trivial subgroups is called decomposable, and if a group cannot be expressed as such a direct sum then it is called indecomposable.
In mathematics, specifically ring theory, a principal ideal is an ideal in a ring that is generated by a single element of through multiplication by every element of The term also has another, similar meaning in order theory, where it refers to an (order) ideal in a poset generated by a single element which is to say the set of all elements less than or equal to in
In mathematics, a free abelian group is an abelian group with a basis. Being an abelian group means that it is a set with an addition operation that is associative, commutative, and invertible. A basis, also called an integral basis, is a subset such that every element of the group can be uniquely expressed as an integer combination of finitely many basis elements. For instance the two-dimensional integer lattice forms a free abelian group, with coordinatewise addition as its operation, and with the two points (1,0) and (0,1) as its basis. Free abelian groups have properties which make them similar to vector spaces, and may equivalently be called free-modules, the free modules over the integers. Lattice theory studies free abelian subgroups of real vector spaces. In algebraic topology, free abelian groups are used to define chain groups, and in algebraic geometry they are used to define divisors.

In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem, and uses a specified set of generators for the group. It is a central tool in combinatorial and geometric group theory. The structure and symmetry of Cayley graphs makes them particularly good candidates for constructing families of expander graphs.

In mathematics, the order of a finite group is the number of its elements. If a group is not finite, one says that its order is infinite. The order of an element of a group is the order of the subgroup generated by the element. If the group operation is denoted as a multiplication, the order of an element a of a group, is thus the smallest positive integer m such that am = e, where e denotes the identity element of the group, and am denotes the product of m copies of a. If no such m exists, the order of a is infinite.
In abstract algebra, the free monoid on a set is the monoid whose elements are all the finite sequences of zero or more elements from that set, with string concatenation as the monoid operation and with the unique sequence of zero elements, often called the empty string and denoted by ε or λ, as the identity element. The free monoid on a set A is usually denoted A∗. The free semigroup on A is the subsemigroup of A∗ containing all elements except the empty string. It is usually denoted A+.
In mathematics, the Grothendieck group, or group of differences, of a commutative monoid M is a certain abelian group. This abelian group is constructed from M in the most universal way, in the sense that any abelian group containing a homomorphic image of M will also contain a homomorphic image of the Grothendieck group of M. The Grothendieck group construction takes its name from a specific case in category theory, introduced by Alexander Grothendieck in his proof of the Grothendieck–Riemann–Roch theorem, which resulted in the development of K-theory. This specific case is the monoid of isomorphism classes of objects of an abelian category, with the direct sum as its operation.
In algebra, a presentation of a monoid is a description of a monoid in terms of a set Σ of generators and a set of relations on the free monoid Σ∗ generated by Σ. The monoid is then presented as the quotient of the free monoid by these relations. This is an analogue of a group presentation in group theory.
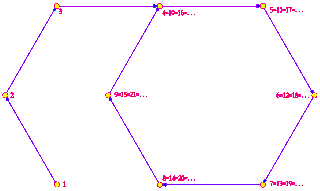
In mathematics, a monogenic semigroup is a semigroup generated by a single element. Monogenic semigroups are also called cyclic semigroups.
Gordan's lemma is a lemma in convex geometry and algebraic geometry. It can be stated in several ways.
In computer science, more precisely in automata theory, a recognizable set of a monoid is a subset that can be distinguished by some morphism to a finite monoid. Recognizable sets are useful in automata theory, formal languages and algebra.
In computer science, more precisely in automata theory, a rational set of a monoid is an element of the minimal class of subsets of this monoid that contains all finite subsets and is closed under union, product and Kleene star. Rational sets are useful in automata theory, formal languages and algebra.
In mathematics, and more precisely in semigroup theory, a variety of finite semigroups is a class of semigroups having some nice algebraic properties. Those classes can be defined in two distinct ways, using either algebraic notions or topological notions. Varieties of finite monoids, varieties of finite ordered semigroups and varieties of finite ordered monoids are defined similarly.
In mathematics, and more precisely in semigroup theory, a nilsemigroup or nilpotent semigroup is a semigroup whose every element is nilpotent.






























