List of planar symmetry groups

This article summarizes the classes of discrete symmetry groups of the Euclidean plane. The symmetry groups are named here by three naming schemes: International notation, orbifold notation, and Coxeter notation. There are three kinds of symmetry groups of the plane:

• 2 families of rosette groups – 2D point groups
• 7 frieze groups – 2D line groups
• 17 wallpaper groups – 2D space groups.

Rosette groups

There are two families of discrete two-dimensional point groups, and they are specified with parameter n, which is the order of the group of the rotations in the group.

Family	Intl (orbifold)	Schön.	Geo [1] Coxeter	Order	Examples
Cyclic symmetry	n (n•)	Cn	n [n]+	n	C1, [ ]+ (•)	C2, [2]+ (2•)	C3, [3]+ (3•)	C4, [4]+ (4•)	C5, [5]+ (5•)	C6, [6]+ (6•)
Dihedral symmetry	nm (*n•)	Dn	n [n]	2n	D1, [ ] (*•)	D2, [2] (*2•)	D3, [3] (*3•)	D4, [4] (*4•)	D5, [5] (*5•)	D6, [6] (*6•)

Frieze groups

The 7 frieze groups, the two-dimensional line groups, with a direction of periodicity are given with five notational names. The Schönflies notation is given as infinite limits of 7 dihedral groups. The yellow regions represent the infinite fundamental domain in each.

[1,∞], IUC (orbifold) Geo Schönflies Coxeter Fundamental domain Example p1m1 (*∞•) p1 C∞v [1,∞] sidle p1 (∞•) p1 C∞ [1,∞]+ hop [2,∞+], IUC (orbifold) Geo Schönflies Coxeter Fundamental domain Example p11m (∞*) p. 1 C∞h [2,∞+] jump p11g (∞×) p.g1 S2∞ [2+,∞+] step

[2,∞], IUC (orbifold) Geo Schönflies Coxeter Fundamental domain Example p2mm (*22∞) p2 D∞h [2,∞] spinning jump p2mg (2*∞) p2g D∞d [2+,∞] spinning sidle p2 (22∞) p2 D∞ [2,∞]+ spinning hop

Wallpaper groups

The 17 wallpaper groups, with finite fundamental domains, are given by International notation, orbifold notation, and Coxeter notation, classified by the 5 Bravais lattices in the plane: square, oblique (parallelogrammatic), hexagonal (equilateral triangular), rectangular (centered rhombic), and rhombic (centered rectangular).

The p1 and p2 groups, with no reflectional symmetry, are repeated in all classes. The related pure reflectional Coxeter group are given with all classes except oblique.

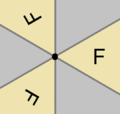
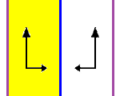
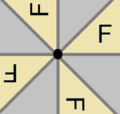
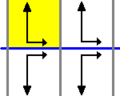
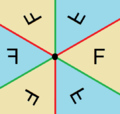
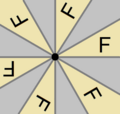
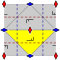
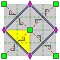
Square [4,4], IUC (Orb.) Geo Coxeter Domain Conway name p1 (°) p1 Monotropic p2 (2222) p2 [4,1+,4]+ [1+,4,4,1+]+ Ditropic pgg (22×) pg2g [4+,4+] Diglide pmm (*2222) p2 [4,1+,4] [1+,4,4,1+] Discopic cmm (2*22) c2 [(4,4,2+)] Dirhombic p4 (442) p4 [4,4]+ Tetratropic p4g (4*2) pg4 [4+,4] Tetragyro p4m (*442) p4 [4,4] Tetrascopic

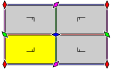
Rectangular [∞h,2,∞v], IUC (Orb.) Geo Coxeter Domain Conway name p1 (°) p1 [∞+,2,∞+] Monotropic p2 (2222) p2 [∞,2,∞]+ Ditropic pg(h) (××) pg1 h: [∞+,(2,∞)+] Monoglide pg(v) (××) pg1 v: [(∞,2)+,∞+] Monoglide pgm (22*) pg2 h: [(∞,2)+,∞] Digyro pmg (22*) pg2 v: [∞,(2,∞)+] Digyro pm(h) (**) p1 h: [∞+,2,∞] Monoscopic pm(v) (**) p1 v: [∞,2,∞+] Monoscopic pmm (*2222) p2 [∞,2,∞] Discopic

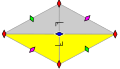
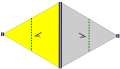
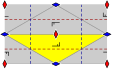
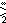Rhombic [∞h,2+,∞v], IUC (Orb.) Geo Coxeter Domain Conway name p1 (°) p1 [∞+,2+,∞+] Monotropic p2 (2222) p2 [∞,2+,∞]+ Ditropic cm(h) (*×) c1 h: [∞+,2+,∞] Monorhombic cm(v) (*×) c1 v: [∞,2+,∞+] Monorhombic pgg (22×) pg2g [((∞,2)+)[2]] Diglide cmm (2*22) c2 [∞,2+,∞] Dirhombic Parallelogrammatic (oblique) p1 (°) p1 Monotropic p2 (2222) p2 Ditropic

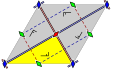
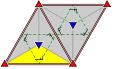
Hexagonal/Triangular [6,3], / [3[3]], IUC (Orb.) Geo Coxeter Domain Conway name p1 (°) p1 Monotropic p2 (2222) p2 [6,3]Δ Ditropic cmm (2*22) c2 [6,3]⅄ Dirhombic p3 (333) p3 [1+,6,3+] [3[3]]+ Tritropic p3m1 (*333) p3 [1+,6,3] [3[3]] Triscopic p31m (3*3) h3 [6,3+] Trigyro p6 (632) p6 [6,3]+ Hexatropic p6m (*632) p6 [6,3] Hexascopic

Wallpaper subgroup relationships

Subgroup relationships among the 17 wallpaper group ^[2]

		o	2222	××	**	*×	22×	22*	*2222	2*22	442	4*2	*442	333	*333	3*3	632	*632
		p1	p2	pg	pm	cm	pgg	pmg	pmm	cmm	p4	p4g	p4m	p3	p3m1	p31m	p6	p6m
o	p1	2
2222	p2	2	2	2
××	pg	2		2
**	pm	2		2	2	2
*×	cm	2		2	2	3
22×	pgg	4	2	2			3
22*	pmg	4	2	2	2	4	2	3
*2222	pmm	4	2	4	2	4	4	2	2	2
2*22	cmm	4	2	4	4	2	2	2	2	4
442	p4	4	2								2
4*2	p4g	8	4	4	8	4	2	4	4	2	2	9
*442	p4m	8	4	8	4	4	4	4	2	2	2	2	2
333	p3	3												3
*333	p3m1	6		6	6	3								2	4	3
3*3	p31m	6		6	6	3								2	3	4
632	p6	6	3											2			4
*632	p6m	12	6	12	12	6	6	6	6	3				4	2	2	2	3

See also

• List of spherical symmetry groups
• Orbifold notation#Hyperbolic plane - Hyperbolic symmetry groups

Notes

1. The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF
2. Coxeter, (1980), The 17 plane groups, Table 4

References

• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN   978-1-56881-220-5 (Orbifold notation for polyhedra, Euclidean and hyperbolic tilings)
• On Quaternions and Octonions, 2003, John Horton Conway and Derek A. Smith ISBN   978-1-56881-134-5
• Kaleidoscopes: Selected Writings of H. S. M. Coxeter , edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
• Coxeter, H. S. M. & Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN   0-387-09212-9.
• N. W. Johnson: Geometries and Transformations, (2018) ISBN   978-1-107-10340-5 Chapter 12: Euclidean Symmetry Groups

External links

• "Conway's manuscript" on Orbifold notation (Notation changed from this original, x is now used in place of open-dot, and o is used in place of the closed dot)
• The 17 Wallpaper Groups