Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which are called Euclidean n-spaces when one wants to specify their dimension. For n equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.
In elementary geometry, a polytope is a geometric object with flat sides (faces). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions n as an n-dimensional polytope or n-polytope. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope. In this context, "flat sides" means that the sides of a (k + 1)-polytope consist of k-polytopes that may have (k – 1)-polytopes in common.

In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells, meeting at right angles. The tesseract is one of the six convex regular 4-polytopes.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.

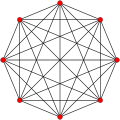
In geometry, a cross-polytope, hyperoctahedron, orthoplex, staurotope, or cocube is a regular, convex polytope that exists in n-dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahedron, and a 4-dimensional cross-polytope is a 16-cell. Its facets are simplexes of the previous dimension, while the cross-polytope's vertex figure is another cross-polytope from the previous dimension.

Four-dimensional space (4D) is the mathematical extension of the concept of three-dimensional space (3D). Three-dimensional space is the simplest possible abstraction of the observation that one needs only three numbers, called dimensions, to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring and multiplying its length, width, and height. This concept of ordinary space is called Euclidean space because it corresponds to Euclid's geometry, which was originally abstracted from the spatial experiences of everyday life.
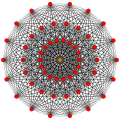
In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8. The name derives from the fact that it is the root lattice of the E8 root system.

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a reflection group. Reflection groups also include Weyl groups and crystallographic Coxeter groups. While the orthogonal group is generated by reflections, it is a continuous group, not a discrete group, and is generally considered separately.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects and a finite number of exceptions — often with desirable properties — that do not fit into any series. These are known as exceptional objects. In many cases, these exceptional objects play a further and important role in the subject. Furthermore, the exceptional objects in one branch of mathematics often relate to the exceptional objects in others.

In six-dimensional geometry, a uniform 6-polytope is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform 5-polytopes.
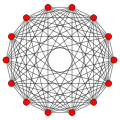
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.

In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted or . It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement.
Six-dimensional space is any space that has six dimensions, six degrees of freedom, and that needs six pieces of data, or coordinates, to specify a location in this space. There are an infinite number of these, but those of most interest are simpler ones that model some aspect of the environment. Of particular interest is six-dimensional Euclidean space, in which 6-polytopes and the 5-sphere are constructed. Six-dimensional elliptical space and hyperbolic spaces are also studied, with constant positive and negative curvature.
In mathematics, a sequence of n real numbers can be understood as a location in n-dimensional space. When n = 8, the set of all such locations is called 8-dimensional space. Often such spaces are studied as vector spaces, without any notion of distance. Eight-dimensional Euclidean space is eight-dimensional space equipped with the Euclidean metric.
In geometry, a (globally) projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids.