In geometry, a cube or regular hexahedron is a three-dimensional solid object bounded by six congruent square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.

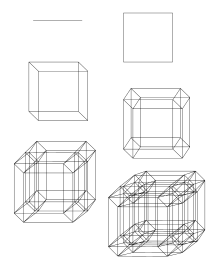
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells, meeting at right angles. The tesseract is one of the six convex regular 4-polytopes.

In geometry, a hypercube is an n-dimensional analogue of a square and a cube ; the special case for n = 4 is known as a tesseract. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.
In geometry, a zonohedron is a convex polyhedron that is centrally symmetric, every face of which is a polygon that is centrally symmetric. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as a three-dimensional projection of a hypercube. Zonohedra were originally defined and studied by E. S. Fedorove, a Russian crystallographer. More generally, in any dimension, the Minkowski sum of line segments forms a polytope known as a zonotope.

In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes. Its opposite is irregular grid.
In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.
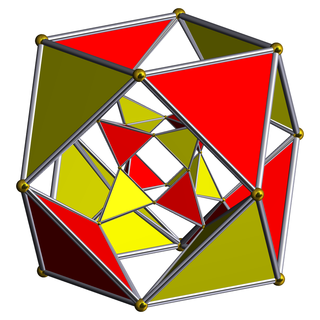
In geometry, the rectified tesseract, rectified 8-cell is a uniform 4-polytope bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra. It has half the vertices of a runcinated tesseract, with its construction, called a runcic tesseract.

In geometry, demihypercubes (also called n-demicubes, n-hemicubes, and half measure polytopes) are a class of n-polytopes constructed from alternation of an n-hypercube, labeled as hγn for being half of the hypercube family, γn. Half of the vertices are deleted and new facets are formed. The 2n facets become 2n(n−1)-demicubes, and 2n(n−1)-simplex facets are formed in place of the deleted vertices.
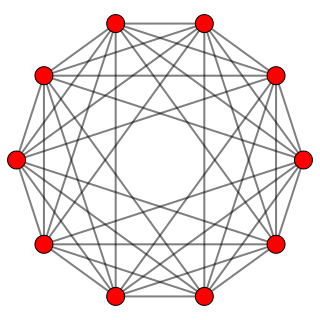
In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.
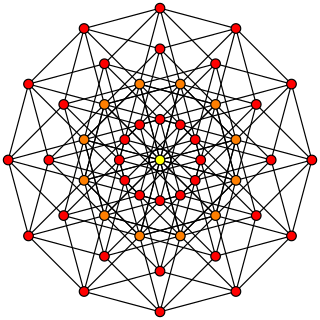
In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces.

In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces.
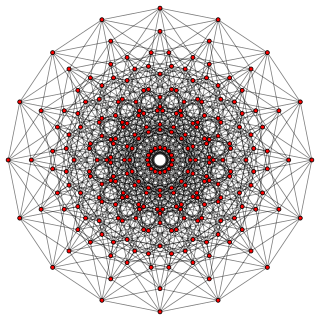
In geometry, an 8-cube is an eight-dimensional hypercube. It has 256 vertices, 1024 edges, 1792 square faces, 1792 cubic cells, 1120 tesseract 4-faces, 448 5-cube 5-faces, 112 6-cube 6-faces, and 16 7-cube 7-faces.

In geometry, a 9-cube is a nine-dimensional hypercube with 512 vertices, 2304 edges, 4608 square faces, 5376 cubic cells, 4032 tesseract 4-faces, 2016 5-cube 5-faces, 672 6-cube 6-faces, 144 7-cube 7-faces, and 18 8-cube 8-faces.
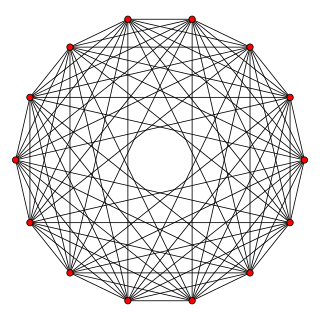
In geometry, a 7-orthoplex, or 7-cross polytope, is a regular 7-polytope with 14 vertices, 84 edges, 280 triangle faces, 560 tetrahedron cells, 672 5-cells 4-faces, 448 5-faces, and 128 6-faces.
In geometry, a hypercubic honeycomb is a family of regular honeycombs (tessellations) in n-dimensional spaces with the Schläfli symbols {4,3...3,4} and containing the symmetry of Coxeter group Rn for n ≥ 3.

In five-dimensional geometry, a truncated 5-cube is a convex uniform 5-polytope, being a truncation of the regular 5-cube.
In six-dimensional geometry, a truncated 6-cube is a convex uniform 6-polytope, being a truncation of the regular 6-cube.