
A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the centre of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.

In mathematics, a frieze or frieze pattern is a two-dimensional design that repeats in one direction. Such patterns occur frequently in architecture and decorative art. Frieze patterns can be classified into seven types according to their symmetries. The set of symmetries of a frieze pattern is called a frieze group.

Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have sign : a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space.

In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space ; that is, the transformations of that space that preserve the Euclidean distance between any two points. The group depends only on the dimension n of the space, and is commonly denoted E(n) or ISO(n).

Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

In geometry, a point group is a mathematical group of symmetry operations that have a fixed point in common. The coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every point group in dimension d is then a subgroup of the orthogonal group O(d). Point groups are used to describe the symmetries of geometric figures and physical objects such as molecules.
In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO(4). The name comes from the fact that it is the special orthogonal group of order 4.
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.

In mathematics, and especially in geometry, an object has icosahedral symmetry if it has the same symmetries as a regular icosahedron. Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron and the rhombic triacontahedron.

A regular octahedron has 24 rotational symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedron that is dual to an octahedron.

A regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dihn.

In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries (isometries) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O(2), including O(2) itself. Its elements are rotations and reflections, and every such group containing only rotations is a subgroup of the special orthogonal group SO(2), including SO(2) itself. That group is isomorphic to R/Z and the first unitary group, U(1), a group also known as the circle group.
In geometry, a (globally) projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids.

In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.
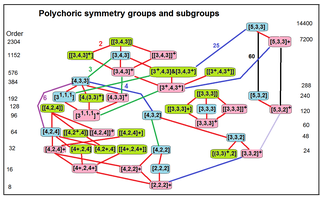
In geometry, a point group in four dimensions is an isometry group in four dimensions that leaves the origin fixed, or correspondingly, an isometry group of a 3-sphere.

In geometry, an object has symmetry if there is an operation or transformation that maps the figure/object onto itself. Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be symmetric under rotation or to have rotational symmetry. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry.




















