In mathematics, the orthogonal group in dimension n, denoted O(n), is the group of distance-preserving transformations of a Euclidean space of dimension n that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of n × n orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact.

In mathematics, the special unitary group of degree n, denoted SU(n), is the Lie group of n × n unitary matrices with determinant 1.

In mathematics, E6 is the name of some closely related Lie groups, linear algebraic groups or their Lie algebras , all of which have dimension 78; the same notation E6 is used for the corresponding root lattice, which has rank 6. The designation E6 comes from the Cartan–Killing classification of the complex simple Lie algebras (see Élie Cartan § Work). This classifies Lie algebras into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled E6, E7, E8, F4, and G2. The E6 algebra is thus one of the five exceptional cases.

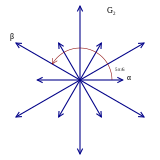
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection group. In fact it turns out that most finite reflection groups are Weyl groups. Abstractly, Weyl groups are finite Coxeter groups, and are important examples of these.
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the geometry of the base manifold using a solder form. Cartan connections describe the geometry of manifolds modelled on homogeneous spaces.

In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8. The designation E8 comes from the Cartan–Killing classification of the complex simple Lie algebras, which fall into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled G2, F4, E6, E7, and E8. The E8 algebra is the largest and most complicated of these exceptional cases.

In mathematics, E7 is the name of several closely related Lie groups, linear algebraic groups or their Lie algebras e7, all of which have dimension 133; the same notation E7 is used for the corresponding root lattice, which has rank 7. The designation E7 comes from the Cartan–Killing classification of the complex simple Lie algebras, which fall into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled E6, E7, E8, F4, and G2. The E7 algebra is thus one of the five exceptional cases.

In mathematics, a reductive group is a type of linear algebraic group over a field. One definition is that a connected linear algebraic group G over a perfect field is reductive if it has a representation that has a finite kernel and is a direct sum of irreducible representations. Reductive groups include some of the most important groups in mathematics, such as the general linear group GL(n) of invertible matrices, the special orthogonal group SO(n), and the symplectic group Sp(2n). Simple algebraic groups and (more generally) semisimple algebraic groups are reductive.

In mathematics, a Cartan subalgebra, often abbreviated as CSA, is a nilpotent subalgebra of a Lie algebra that is self-normalising. They were introduced by Élie Cartan in his doctoral thesis. It controls the representation theory of a semi-simple Lie algebra over a field of characteristic .

In mathematics, a Lie algebra is semisimple if it is a direct sum of simple Lie algebras.
In mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. Given an affine Lie algebra, one can also form the associated affine Kac-Moody algebra, as described below. From a purely mathematical point of view, affine Lie algebras are interesting because their representation theory, like representation theory of finite-dimensional semisimple Lie algebras, is much better understood than that of general Kac–Moody algebras. As observed by Victor Kac, the character formula for representations of affine Lie algebras implies certain combinatorial identities, the Macdonald identities.
In differential geometry, a Lie-algebra-valued form is a differential form with values in a Lie algebra. Such forms have important applications in the theory of connections on a principal bundle as well as in the theory of Cartan connections.

In mathematics, a Hermitian symmetric space is a Hermitian manifold which at every point has an inversion symmetry preserving the Hermitian structure. First studied by Élie Cartan, they form a natural generalization of the notion of Riemannian symmetric space from real manifolds to complex manifolds.
In mathematics, the spin representations are particular projective representations of the orthogonal or special orthogonal groups in arbitrary dimension and signature. More precisely, they are two equivalent representations of the spin groups, which are double covers of the special orthogonal groups. They are usually studied over the real or complex numbers, but they can be defined over other fields.

In mathematics, the classical groups are defined as the special linear groups over the reals , the complex numbers and the quaternions together with special automorphism groups of symmetric or skew-symmetric bilinear forms and Hermitian or skew-Hermitian sesquilinear forms defined on real, complex and quaternionic finite-dimensional vector spaces. Of these, the complex classical Lie groups are four infinite families of Lie groups that together with the exceptional groups exhaust the classification of simple Lie groups. The compact classical groups are compact real forms of the complex classical groups. The finite analogues of the classical groups are the classical groups of Lie type. The term "classical group" was coined by Hermann Weyl, it being the title of his 1939 monograph The Classical Groups.
In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K (often a maximal compact subgroup) that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G. The key examples are the matrix coefficients of the spherical principal series, the irreducible representations appearing in the decomposition of the unitary representation of G on L2(G/K). In this case the commutant of G is generated by the algebra of biinvariant functions on G with respect to K acting by right convolution. It is commutative if in addition G/K is a symmetric space, for example when G is a connected semisimple Lie group with finite centre and K is a maximal compact subgroup. The matrix coefficients of the spherical principal series describe precisely the spectrum of the corresponding C* algebra generated by the biinvariant functions of compact support, often called a Hecke algebra. The spectrum of the commutative Banach *-algebra of biinvariant L1 functions is larger; when G is a semisimple Lie group with maximal compact subgroup K, additional characters come from matrix coefficients of the complementary series, obtained by analytic continuation of the spherical principal series.

In mathematics, the complexification or universal complexification of a real Lie group is given by a continuous homomorphism of the group into a complex Lie group with the universal property that every continuous homomorphism of the original group into another complex Lie group extends compatibly to a complex analytic homomorphism between the complex Lie groups. The complexification, which always exists, is unique up to unique isomorphism. Its Lie algebra is a quotient of the complexification of the Lie algebra of the original group. They are isomorphic if the original group has a quotient by a discrete normal subgroup which is linear.
In mathematics, a mutation, also called a homotope, of a unital Jordan algebra is a new Jordan algebra defined by a given element of the Jordan algebra. The mutation has a unit if and only if the given element is invertible, in which case the mutation is called a proper mutation or an isotope. Mutations were first introduced by Max Koecher in his Jordan algebraic approach to Hermitian symmetric spaces and bounded symmetric domains of tube type. Their functorial properties allow an explicit construction of the corresponding Hermitian symmetric space of compact type as a compactification of a finite-dimensional complex semisimple Jordan algebra. The automorphism group of the compactification becomes a complex subgroup, the complexification of its maximal compact subgroup. Both groups act transitively on the compactification. The theory has been extended to cover all Hermitian symmetric spaces using the theory of Jordan pairs or Jordan triple systems. Koecher obtained the results in the more general case directly from the Jordan algebra case using the fact that only Jordan pairs associated with period two automorphisms of Jordan algebras are required.

This is a glossary for the terminology applied in the mathematical theories of Lie groups and Lie algebras. For the topics in the representation theory of Lie groups and Lie algebras, see Glossary of representation theory. Because of the lack of other options, the glossary also includes some generalizations such as quantum group.
In mathematics, and especially differential geometry and mathematical physics, gauge theory is the general study of connections on vector bundles, principal bundles, and fibre bundles. Gauge theory in mathematics should not be confused with the closely related concept of a gauge theory in physics, which is a field theory which admits gauge symmetry. In mathematics theory means a mathematical theory, encapsulating the general study of a collection of concepts or phenomena, whereas in the physical sense a gauge theory is a mathematical model of some natural phenomenon.