
In algebraic and differential geometry, a Calabi–Yau manifold, also known as a Calabi–Yau space, is a particular type of manifold which has certain properties, such as Ricci flatness, yielding applications in theoretical physics. Particularly in superstring theory, the extra dimensions of spacetime are sometimes conjectured to take the form of a 6-dimensional Calabi–Yau manifold, which led to the idea of mirror symmetry. Their name was coined by Candelas et al. (1985), after Eugenio Calabi, who first conjectured that such surfaces might exist, and Shing-Tung Yau, who proved the Calabi conjecture.

In the mathematical disciplines of topology and geometry, an orbifold is a generalization of a manifold. Roughly speaking, an orbifold is a topological space that is locally a finite group quotient of a Euclidean space.
In physics, Ginzburg–Landau theory, often called Landau–Ginzburg theory, named after Vitaly Ginzburg and Lev Landau, is a mathematical physical theory used to describe superconductivity. In its initial form, it was postulated as a phenomenological model which could describe type-I superconductors without examining their microscopic properties. One GL-type superconductor is the famous YBCO, and generally all cuprates.
T-duality in theoretical physics is an equivalence of two physical theories, which may be either quantum field theories or string theories. In the simplest example of this relationship, one of the theories describes strings propagating in a spacetime shaped like a circle of some radius , while the other theory describes strings propagating on a spacetime shaped like a circle of radius proportional to . The idea of T-duality was first noted by Bala Sathiapalan in an obscure paper in 1987. The two T-dual theories are equivalent in the sense that all observable quantities in one description are identified with quantities in the dual description. For example, momentum in one description takes discrete values and is equal to the number of times the string winds around the circle in the dual description.

In theoretical physics, supergravity is a modern field theory that combines the principles of supersymmetry and general relativity; this is in contrast to non-gravitational supersymmetric theories such as the Minimal Supersymmetric Standard Model. Supergravity is the gauge theory of local supersymmetry. Since the supersymmetry (SUSY) generators form together with the Poincaré algebra a superalgebra, called the super-Poincaré algebra, supersymmetry as a gauge theory makes gravity arise in a natural way.
In differential geometry, a hyperkähler manifold is a Riemannian manifold endowed with three integrable almost complex structures that are Kähler with respect to the Riemannian metric and satisfy the quaternionic relations . In particular, it is a hypercomplex manifold. All hyperkähler manifolds are Ricci-flat and are thus Calabi–Yau manifolds.
In theoretical physics, type I string theory is one of five consistent supersymmetric string theories in ten dimensions. It is the only one whose strings are unoriented and the only one which perturbatively contains not only closed strings, but also open strings. The terminology of type I and type II was coined by John Henry Schwarz in 1982 to classify the three string theories known at the time.
In theoretical physics, type II string theory is a unified term that includes both type IIA strings and type IIB strings theories. Type II string theory accounts for two of the five consistent superstring theories in ten dimensions. Both theories have extended supersymmetry which is maximal amount of supersymmetry — namely 32 supercharges — in ten dimensions. Both theories are based on oriented closed strings. On the worldsheet, they differ only in the choice of GSO projection. They were first discovered by Michael Green and John Henry Schwarz in 1982, with the terminology of type I and type II coined to classify the three string theories known at the time.
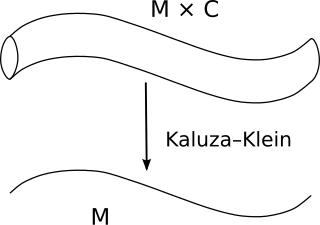
In theoretical physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic.
The SYZ conjecture is an attempt to understand the mirror symmetry conjecture, an issue in theoretical physics and mathematics. The original conjecture was proposed in a paper by Strominger, Yau, and Zaslow, entitled "Mirror Symmetry is T-duality".
In mathematics, a quintic threefold is a 3-dimensional hypersurface of degree 5 in 4-dimensional projective space . Non-singular quintic threefolds are Calabi–Yau manifolds.
In mathematics, specifically algebraic geometry, Donaldson–Thomas theory is the theory of Donaldson–Thomas invariants. Given a compact moduli space of sheaves on a Calabi–Yau threefold, its Donaldson–Thomas invariant is the virtual number of its points, i.e., the integral of the cohomology class 1 against the virtual fundamental class. The Donaldson–Thomas invariant is a holomorphic analogue of the Casson invariant. The invariants were introduced by Simon Donaldson and Richard Thomas. Donaldson–Thomas invariants have close connections to Gromov–Witten invariants of algebraic three-folds and the theory of stable pairs due to Rahul Pandharipande and Thomas.
This page is a glossary of terms in string theory, including related areas such as supergravity, supersymmetry, and high energy physics.
In mathematics, topological recursion is a recursive definition of invariants of spectral curves. It has applications in enumerative geometry, random matrix theory, mathematical physics, string theory, knot theory.
In string theory, the Ramond–Neveu–Schwarz (RNS) formalism is an approach to formulating superstrings in which the worldsheet has explicit superconformal invariance but spacetime supersymmetry is hidden, in contrast to the Green–Schwarz formalism where the latter is explicit. It was originally developed by Pierre Ramond, André Neveu and John Schwarz in the RNS model in 1971, which gives rise to type II string theories and can also give type I string theory. Heterotic string theories can also be acquired through this formalism by using a different worldsheet action. There are various ways to quantize the string within this framework including light-cone quantization, old canonical quantization, and BRST quantization. A consistent string theory is only acquired if the spectrum of states is restricted through a procedure known as a GSO projection, with this projection being automatically present in the Green–Schwarz formalism.
In mathematics and theoretical physics, and especially gauge theory, the deformed Hermitian Yang–Mills (dHYM) equation is a differential equation describing the equations of motion for a D-brane in the B-model of string theory. The equation was derived by Mariño-Minasian-Moore-Strominger in the case of Abelian gauge group, and by Leung–Yau–Zaslow using mirror symmetry from the corresponding equations of motion for D-branes in the A-model of string theory.
In mathematics, and especially differential geometry and mathematical physics, gauge theory is the general study of connections on vector bundles, principal bundles, and fibre bundles. Gauge theory in mathematics should not be confused with the closely related concept of a gauge theory in physics, which is a field theory that admits gauge symmetry. In mathematics theory means a mathematical theory, encapsulating the general study of a collection of concepts or phenomena, whereas in the physical sense a gauge theory is a mathematical model of some natural phenomenon.
In mathematics, mirror symmetry is a conjectural relationship between certain Calabi–Yau manifolds and a constructed "mirror manifold". The conjecture allows one to relate the number of rational curves on a Calabi-Yau manifold to integrals from a family of varieties. In short, this means there is a relation between the number of genus algebraic curves of degree on a Calabi-Yau variety and integrals on a dual variety . These relations were original discovered by Candelas, de la Ossa, Green, and Parkes in a paper studying a generic quintic threefold in as the variety and a construction from the quintic Dwork family giving . Shortly after, Sheldon Katz wrote a summary paper outlining part of their construction and conjectures what the rigorous mathematical interpretation could be.
In supersymmetry, eleven-dimensional supergravity is the theory of supergravity in the highest number of dimensions allowed for a supersymmetric theory. It contains a graviton, a gravitino, and a 3-form gauge field, with their interactions uniquely fixed by supersymmetry. Discovered in 1978 by Eugène Cremmer, Bernard Julia, and Joël Scherk, it quickly became a popular candidate for a theory of everything during the 1980s. However, interest in it soon faded due to numerous difficulties that arise when trying to construct physically realistic models. It came back to prominence in the mid-1990s when it was found to be the low energy limit of M-theory, making it crucial for understanding various aspects of string theory.
In supersymmetry, type IIB supergravity is the unique supergravity in ten dimensions with two supercharges of the same chirality. It was first constructed in 1983 by John Schwarz and independently by Paul Howe and Peter West at the level of its equations of motion. While it does not admit a fully covariant action due to the presence of a self-dual field, it can be described by an action if the self-duality condition is imposed by hand on the resulting equations of motion. The other types of supergravity in ten dimensions are type IIA supergravity, which has two supercharges of opposing chirality, and type I supergravity, which has a single supercharge. The theory plays an important role in modern physics since it is the low-energy limit of type IIB string theory.























