M-theory is a theory in physics that unifies all consistent versions of superstring theory. Edward Witten first conjectured the existence of such a theory at a string theory conference at the University of Southern California in 1995. Witten's announcement initiated a flurry of research activity known as the second superstring revolution. Prior to Witten's announcement, string theorists had identified five versions of superstring theory. Although these theories initially appeared to be very different, work by many physicists showed that the theories were related in intricate and nontrivial ways. Physicists found that apparently distinct theories could be unified by mathematical transformations called S-duality and T-duality. Witten's conjecture was based in part on the existence of these dualities and in part on the relationship of the string theories to a field theory called eleven-dimensional supergravity.
In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and interact with each other. On distance scales larger than the string scale, a string looks just like an ordinary particle, with its mass, charge, and other properties determined by the vibrational state of the string. In string theory, one of the many vibrational states of the string corresponds to the graviton, a quantum mechanical particle that carries the gravitational force. Thus, string theory is a theory of quantum gravity.

In algebraic geometry, a Calabi–Yau manifold, also known as a Calabi–Yau space, is a particular type of manifold which has properties, such as Ricci flatness, yielding applications in theoretical physics. Particularly in superstring theory, the extra dimensions of spacetime are sometimes conjectured to take the form of a 6-dimensional Calabi–Yau manifold, which led to the idea of mirror symmetry. Their name was coined by Candelas et al. (1985), after Eugenio Calabi who first conjectured that such surfaces might exist, and Shing-Tung Yau (1978) who proved the Calabi conjecture.
In theoretical physics, T-duality is an equivalence of two physical theories, which may be either quantum field theories or string theories. In the simplest example of this relationship, one of the theories describes strings propagating in a spacetime shaped like a circle of some radius , while the other theory describes strings propagating on a spacetime shaped like a circle of radius proportional to . The idea of T-duality was first noted by Bala Sathiapalan in an obscure paper in 1987. The two T-dual theories are equivalent in the sense that all observable quantities in one description are identified with quantities in the dual description. For example, momentum in one description takes discrete values and is equal to the number of times the string winds around the circle in the dual description.

In theoretical physics, supergravity is a modern field theory that combines the principles of supersymmetry and general relativity; this is in contrast to non-gravitational supersymmetric theories such as the Minimal Supersymmetric Standard Model. Supergravity is the gauge theory of local supersymmetry. Since the supersymmetry (SUSY) generators form together with the Poincaré algebra a superalgebra, called the super-Poincaré algebra, supersymmetry as a gauge theory makes gravity arise in a natural way.
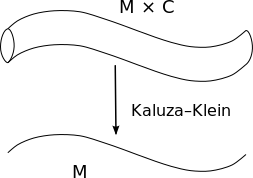
In particle physics, the hypothetical dilaton particle is a particle of a scalar field that appears in theories with extra dimensions when the volume of the compactified dimensions varies. It appears as a radion in Kaluza–Klein theory's compactifications of extra dimensions. In Brans–Dicke theory of gravity, Newton's constant is not presumed to be constant but instead 1/G is replaced by a scalar field and the associated particle is the dilaton.
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.
In mathematics and string theory, a conifold is a generalization of a manifold. Unlike manifolds, conifolds can contain conical singularities, i.e. points whose neighbourhoods look like cones over a certain base. In physics, in particular in flux compactifications of string theory, the base is usually a five-dimensional real manifold, since the typically considered conifolds are complex 3-dimensional spaces.
In theoretical physics, F-theory is a branch of string theory developed by Iranian physicist Cumrun Vafa. The new vacua described by F-theory were discovered by Vafa and allowed string theorists to construct new realistic vacua — in the form of F-theory compactified on elliptically fibered Calabi–Yau four-folds. The letter "F" supposedly stands for "Father".

Nathan "Nati" Seiberg is an Israeli American theoretical physicist who works on quantum field theory and string theory. He is currently a professor at the Institute for Advanced Study in Princeton, New Jersey, United States.
In theoretical physics orientifold is a generalization of the notion of orbifold, proposed by Augusto Sagnotti in 1987. The novelty is that in the case of string theory the non-trivial element(s) of the orbifold group includes the reversal of the orientation of the string. Orientifolding therefore produces unoriented strings—strings that carry no "arrow" and whose two opposite orientations are equivalent. Type I string theory is the simplest example of such a theory and can be obtained by orientifolding type IIB string theory.
Homological mirror symmetry is a mathematical conjecture made by Maxim Kontsevich. It seeks a systematic mathematical explanation for a phenomenon called mirror symmetry first observed by physicists studying string theory.
In string theory, the string theory landscape is the collection of possible false vacua, together comprising a collective "landscape" of choices of parameters governing compactifications.
In theoretical physics, topological string theory is a version of string theory. Topological string theory appeared in papers by theoretical physicists, such as Edward Witten and Cumrun Vafa, by analogy with Witten's earlier idea of topological quantum field theory.
In string theory, K-theory classification refers to a conjectured application of K-theory to superstrings, to classify the allowed Ramond–Ramond field strengths as well as the charges of stable D-branes.
The SYZ conjecture is an attempt to understand the mirror symmetry conjecture, an issue in theoretical physics and mathematics. The original conjecture was proposed in a paper by Strominger, Yau, and Zaslow, entitled "Mirror Symmetry is T-duality".
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modeling them as vibrations of tiny supersymmetric strings.
In string theory and related theories such as supergravity theories, a brane is a physical object that generalizes the notion of a point particle to higher dimensions. Branes are dynamical objects which can propagate through spacetime according to the rules of quantum mechanics. They have mass and can have other attributes such as charge.
A purely combinatorial approach to mirror symmetry was suggested by Victor Batyrev using the polar duality for -dimensional convex polyhedra. The most famous examples of the polar duality provide Platonic solids: e.g., the cube is dual to octahedron, the dodecahedron is dual to icosahedron. There is a natural bijection between the -dimensional faces of a -dimensional convex polyhedron and -dimensional faces of the dual polyhedron and one has . In Batyrev's combinatorial approach to mirror symmetry the polar duality is applied to special -dimensional convex lattice polytopes which are called reflexive polytopes.
Paul Stephen Aspinwall is a British theoretical physicist and mathematician, who works on string theory and also algebraic geometry.