| Set of birotundae | |
|---|---|
 Example: pentagonal orthobirotunda | |
| Faces | 2 n-gons 2n pentagons 4n triangles |
| Edges | 12n |
| Vertices | 6n |
| Symmetry group | Ortho: Dnh, [n,2], (*n22), order 4n Gyro: Dnd, [2n,2+ ], (2*n), order 4n |
| Rotation group | Dn, [n,2]+, (n22), order 2n |
| Properties | convex |
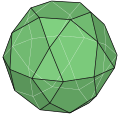
In geometry, a birotunda is any member of a family of dihedral-symmetric polyhedra, formed from two rotunda adjoined through the largest face. They are similar to a bicupola but instead of alternating squares and triangles, it alternates pentagons and triangles around an axis. There are two forms, ortho- and gyro-: an orthobirotunda has one of the two rotundas is placed as the mirror reflection of the other, while in a gyrobirotunda one rotunda is twisted relative to the other.
Contents
The pentagonal birotundas can be formed with regular faces, one a Johnson solid, the other a semiregular polyhedron:
- pentagonal orthobirotunda,
- pentagonal gyrobirotunda, which is also called an icosidodecahedron.
Other forms can be generated with dihedral symmetry and distorted equilateral pentagons.