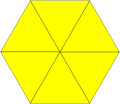
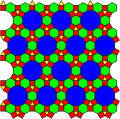
[36; 33434; (3446)2; 46.12] | 
[36; 33434; 3446; (46.12)2] | 
[36; 33434; 3464; (46.12)2] | 
[36; 3342; (334.12)2; 3464] | 
[36; (3342)2; 334.12; 3464] |

[36; 33434; (334.12)2; 3464] | 
[36; 33434; 334.12; (3.12.12)2] | 
[36; 346; (3342)2; 334.12] | 
[36; 33434; 343.12; (3.12.12)2] | 
[(3342)2; 334.12; 343.12; 3.12.12] |

[(3342)2; 334.12; 343.12; 3.12.12] | 
[(3342)2; 334.12; 343.12; 44] | 
[33434; 3262; (3446)2; 44] | 
[36; (3342)2; 33434; 44] | 
[346; (3342)2; 33434; 44] |

[36; 3342; (3464)2; 3446] | 
[3342; 3262; 3464; (3446)2] | 
[33434; 3262; 3464; (3446)2] | 
[36; 33434; (3446)2; 3636] | 
[3342; 33434; 3464; (3446)2] |

[36; 33434; (3262)2; 3446] | 
[3342; 3262; (3464)2; 3446] | 
[33434; 3262; (3464)2; 3446] | 
[346; 3342; (3464)2; 3446] | 
[36; (3342)2; 33434; 3464] |

[36; (3342)2; 33434; 3464] | 
[36; 3342; (33434)2; 3464] | 
[(36)2; 3342; 33434; 3464] | 
[36; 3342; (33434)2; 3464] | 
[(36)2; 3342; 33434; 334.12] |

[36; 33434; (334.12)2; 343.12] | 
[(36)2; 346; 3342; 33434] | 
[(36)2; 346; 3262; 63] | 
[36; (346)2; 3262; 63] | 
[(36)2; 346; 3262; 3636] |

[36; 346; (3262)2; 3636] | 
[36; (346)2; 3262; 3636] | 
[(36)2; 346; 3262; 3636] | 
[36; 346; 3262; (3636)2] | 
[36; (346)2; 3262; 3636] |

[36; (346)2; 3262; 3636] | 
[36; (346)2; 3262; 3636] | 
[36; 346; (3262)2; 3636] | 
[36; 346; (3262)2; 3636] | 
[36; 346; 3262; (63)2] |

[36; 346; (3262)2; 63] | 
[346; (3262)2; 3636; 63] | 
[(346)2; 3262; 3636; 63] | 
[(36)2; 346; 3262; 63] | 
[(36)2; 346; 3262; 63] |

[36; 346; 3262; (63)2] | 
[36; 346; 3262; (63)2] | 
[36; 346; 3262; (63)2] | 
[36; 346; (3262)2; 63] | 
[346; (3262)2; 3636; 63] |

[346; (3262)2; 3636; 63] | 
[346; (3262)2; 3636; 63] | 
[346; 3262; 3636; (63)2] | 
[346; (3262)2; 3636; 63] | 
[3342; 3262; 3446; (63)2] |

[3342; 3262; 3446; (63)2] | 
[3262; 3446; 3636; (44)2] | 
[3262; 3446; 3636; (44)2] | 
[3262; 3446; (3636)2; 44] | 
[3262; 3446; (3636)2; 44] |

[3342; 3262; 3446; (44)2] | 
[346; 3342; 3446; (44)2] | 
[3262; 3446; 3636; (44)2] | 
[3262; 3446; 3636; (44)2] | 
[3262; 3446; (3636)2; 44] |

[3262; 3446; (3636)2; 44] | 
[3342; 3262; 3446; (44)2] | 
[346; 3342; 3446; (44)2] | 
[346; (3342)2; 3636; 44] | 
[36; 3342; (3446)2; 3636] |

[346; (3342)2; 3446; 3636] | 
[346; (3342)2; 3446; 3636] | 
[(36)2; 346; 3446; 3636] | 
[36; 3342; (3446)2; 3636] | 
[346; (3342)2; 3446; 3636] |

[346; (3342)2; 3446; 3636] | 
[(36)2; 346; 3446; 3636] | 
[(36)2; 3342; 3446; 3636] | 
[36; 3342; 3446; (3636)2] | 
[346; 3342; (3446)2; 3636] |

[36; 346; (3342)2; 3446] | 
[346; (3342)2; 3262; 3636] | 
[346; (3342)2; 3262; 3636] | 
[36; (346)2; 3342; 3446] | 
[36; (346)2; 3342; 3446] |

[36; (346)2; 3342; 3446] | 
[36; 346; (3342)2; 3262] | 
[(36)2; 346; 3342; 3636] | 
[(36)2; 346; 3342; 3636] |