
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.
In geometry, a polytope or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces.

Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his Harmonices Mundi.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.

In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.

In geometry, the truncated trihexagonal tiling is one of eight semiregular tilings of the Euclidean plane. There are one square, one hexagon, and one dodecagon on each vertex. It has Schläfli symbol of tr{3,6}.

In geometry, the truncated square tiling is a semiregular tiling by regular polygons of the Euclidean plane with one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon. It has Schläfli symbol of t{4,4}.

In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr{3,6}.

In geometry, the snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex. It has Schläfli symbol sr{3,6}. The snub tetrahexagonal tiling is a related hyperbolic tiling with Schläfli symbol sr{4,6}.
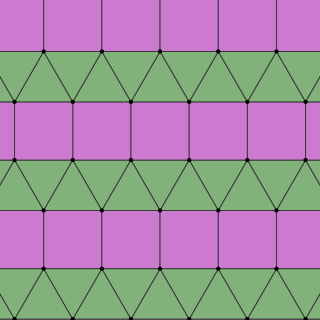
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.

In geometry, the snub square tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. Its Schläfli symbol is s{4,4}.
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-transitive.
In geometry, a uniform honeycomb or uniform tessellation or infinite uniform polytope, is a vertex-transitive honeycomb made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex. Its dimension can be clarified as n-honeycomb for an n-dimensional honeycomb.
In geometry, the demiregular tilings are a set of Euclidean tessellations made from 2 or more regular polygon faces. Different authors have listed different sets of tilings. A more systematic approach looking at symmetry orbits are the 2-uniform tilings of which there are 20. Some of the demiregular ones are actually 3-uniform tilings.

In geometry of the Euclidean plane, the 3-4-6-12 tiling is one of 20 2-uniform tilings of the Euclidean plane by regular polygons, containing regular triangles, squares, hexagons and dodecagons, arranged in two vertex configuration: 3.4.6.4 and 4.6.12.

In geometry, a planigon is a convex polygon that can fill the plane with only copies of itself. In the Euclidean plane there are 3 regular planigons; equilateral triangle, squares, and regular hexagons; and 8 semiregular planigons; and 4 demiregular planigons which can tile the plane only with other planigons.

In geometry of the Euclidean plane, the 3-4-3-12 tiling is one of 20 2-uniform tilings of the Euclidean plane by regular polygons, containing regular triangles, squares, and dodecagons, arranged in two vertex configuration: 3.4.3.12 and 3.12.12.



























