Truncated order-4 hexagonal tiling

Last updated March 22, 2019

Truncated order-4 hexagonal tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	4.12.12
Schläfli symbol	t{6,4} tr{6,6} or $t{\begin{Bmatrix}6\\6\end{Bmatrix}}$
Wythoff symbol	2 4 \| 6 2 6 6 \|
Coxeter diagram	or
Symmetry group	[6,4], (642) [6,6], (662)
Dual	Order-6 tetrakis square tiling
Properties	Vertex-transitive

In geometry, the truncated order-4 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{6,4}. A secondary construction tr{6,6} is called a truncated hexahexagonal tiling with two colors of dodecagons.

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

Hyperbolic geometry Non-Euclidean geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

Schläfli symbol notation that defines regular polytopes and tessellations

In geometry, the Schläfli symbol is a notation of the form {p,q,r,...} that defines regular polytopes and tessellations.

Constructions

There are two uniform constructions of this tiling, first from [6,4] kaleidoscope, and a lower symmetry by removing the last mirror, [6,4,1⁺], gives [6,6], (*662).

A kaleidoscope is an optical instrument with two or more reflecting surfaces tilted to each other in an angle, so that one or more objects on one end of the mirrors are seen as a regular symmetrical pattern when viewed from the other end, due to repeated reflection. The reflectors are usually enclosed in a tube, often containing on one end a cell with loose, colored pieces of glass or other transparent materials to be reflected into the viewed pattern. Rotation of the cell causes motion of the materials, resulting in an ever-changing view being presented.

Two uniform constructions of 4.6.4.6
Name	Tetrahexagonal	Truncated hexahexagonal
Image
Symmetry	[6,4] (*642)	[6,6] = [6,4,1⁺] (*662) =
Symbol	t{6,4}	tr{6,6}
Coxeter diagram

Dual tiling


The dual tiling, order-6 tetrakis square tiling has face configuration V4.12.12, and represents the fundamental domains of the [6,6] symmetry group.

Related polyhedra and tiling

*n42 symmetry mutation of truncated tilings: 4.2n.2n
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Truncated figures
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
n-kis figures
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Uniform tetrahexagonal tilings
*Symmetry: [6,4], (642)** (with [6,6] (662), [(4,3,3)] (443) , [∞,3,∞] (3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (3232) index 4 subsymmetry)
= = =	=	= = =	=	= = =	=

{6,4}	t{6,4}	r{6,4}	t{4,6}	{4,6}	rr{6,4}	tr{6,4}
Uniform duals


V6⁴	V4.12.12	V(4.6)²	V6.8.8	V4⁶	V4.4.4.6	V4.8.12
Alternations
[1⁺,6,4] (*443)	[6⁺,4] (6*2)	[6,1⁺,4] (*3222)	[6,4⁺] (4*3)	[6,4,1⁺] (*662)	[(6,4,2⁺)] (2*32)	[6,4]⁺ (642)
=	=	=	=	=	=

h{6,4}	s{6,4}	hr{6,4}	s{4,6}	h{4,6}	hrr{6,4}	sr{6,4}

Uniform hexahexagonal tilings
Symmetry: [6,6], (*662)
= =	= =	= =	= =	= =	= =	= =

{6,6} = h{4,6}	t{6,6} = h₂{4,6}	r{6,6} {6,4}	t{6,6} = h₂{4,6}	{6,6} = h{4,6}	rr{6,6} r{6,4}	tr{6,6} t{6,4}
Uniform duals


V6⁶	V6.12.12	V6.6.6.6	V6.12.12	V6⁶	V4.6.4.6	V4.12.12
Alternations
[1⁺,6,6] (*663)	[6⁺,6] (6*3)	[6,1⁺,6] (*3232)	[6,6⁺] (6*3)	[6,6,1⁺] (*663)	[(6,6,2⁺)] (2*33)	[6,6]⁺ (662)
=		=		=


h{6,6}	s{6,6}	hr{6,6}	s{6,6}	h{6,6}	hrr{6,6}	sr{6,6}

Symmetry

The dual of the tiling represents the fundamental domains of (*662) orbifold symmetry. From [6,6] (*662) symmetry, there are 15 small index subgroup (12 unique) by mirror removal and alternation operators. Mirrors can be removed if its branch orders are all even, and cuts neighboring branch orders in half. Removing two mirrors leaves a half-order gyration point where the removed mirrors met. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The subgroup index-8 group, [1⁺,6,1⁺,6,1⁺] (3333) is the commutator subgroup of [6,6].

In geometry, orbifold notation is a system, invented by William Thurston and popularized by the mathematician John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature. The advantage of the notation is that it describes these groups in a way which indicates many of the groups' properties: in particular, it describes the orbifold obtained by taking the quotient of Euclidean space by the group under consideration.

In geometry, an alternation or partial truncation, is an operation on a polygon, polyhedron, tiling, or higher dimensional polytope that removes alternate vertices.

In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group.

Larger subgroup constructed as [6,6^*], removing the gyration points of (6*3), index 12 becomes (*333333).

The symmetry can be doubled to 642 symmetry by adding a mirror to bisect the fundamental domain.

Small index subgroups of [6,6] (*662)
Index	1	2			4
Diagram
Coxeter	[6,6]	[1⁺,6,6] =	[6,6,1⁺] =	[6,1⁺,6] =	[1⁺,6,6,1⁺] =	[6⁺,6⁺]
Orbifold	*662	*663		*3232	*3333	33×
Direct subgroups
Diagram
Coxeter		[6,6⁺]	[6⁺,6]	[(6,6,2⁺)]	[6,1⁺,6,1⁺] = = = =	[1⁺,6,1⁺,6] = = = =
Orbifold		6*3		2*33	3*33
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[6,6]⁺	[6,6⁺]⁺ =	[6⁺,6]⁺ =	[6,1⁺,6]⁺ =	[6⁺,6⁺]⁺ = [1⁺,6,1⁺,6]⁺ = = =
Orbifold	662	663		3232	3333
Radical subgroups
Index		12		24
Diagram
Coxeter		[6,6*]	[6*,6]	[6,6*]⁺	[6*,6]⁺
Orbifold		*333333		333333

Related Research Articles

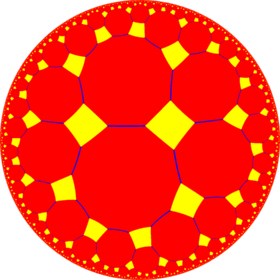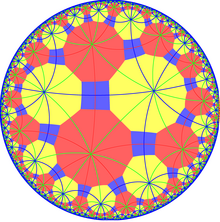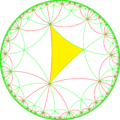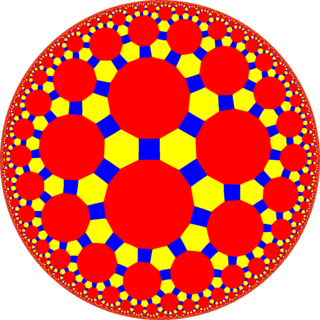
In geometry, the truncated trioctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one hexagon, and one hexadecagon (16-sides) on each vertex. It has Schläfli symbol of tr{8,3}.

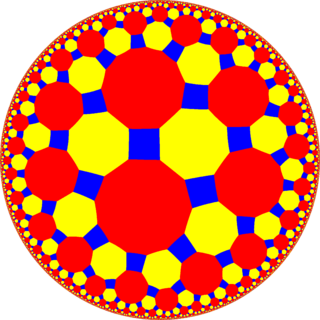
In geometry, the truncated tetrahexagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one octagon, and one dodecagon on each vertex. It has Schläfli symbol of tr{6,4}.

In geometry, the truncated order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{4,6}.

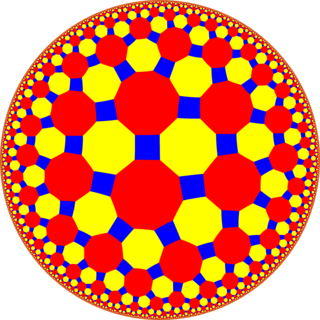
In geometry, the truncated tetrapentagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t_0,1,2{4,5} or tr{4,5}.

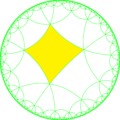
In geometry, the order-8 triangular tiling is a regular tiling of the hyperbolic plane. It is represented by Schläfli symbol of {3,8}, having eight regular triangles around each vertex.

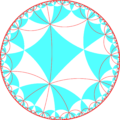
In geometry, the truncated order-8 triangular tiling is a semiregular tiling of the hyperbolic plane. There are two hexagons and one octagon on each vertex. It has Schläfli symbol of t{3,8}.

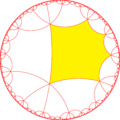
In geometry, the truncated order-6 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{6,6}. It can also be identically constructed as a cantic order-6 square tiling, h₂{4,6}

In geometry, the truncated tetraheptagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of tr{4,7}.

In geometry, the truncated order-4 octagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t_0,1{8,4}. A secondary construction t_0,1,2{8,8} is called a truncated octaoctagonal tiling with two colors of hexakaidecagons.

In geometry, the truncated tetraoctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one octagon, and one hexakaidecagon on each vertex. It has Schläfli symbol of tr{8,4}.

In geometry, the truncated order-8 octagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t_0,1{8,8}.

In geometry, the order-3 apeirogonal tiling is a regular tiling of the hyperbolic plane. It is represented by the Schläfli symbol {∞,3}, having three regular apeirogons around each vertex. Each apeirogon is inscribed in a horocycle.

In geometry, the truncated triapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of tr{∞,3}.

In geometry, the truncated order-4 apeirogonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{∞,4}.

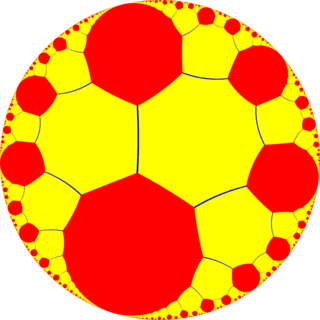
In geometry, the truncated infinite-order square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{4,∞}.

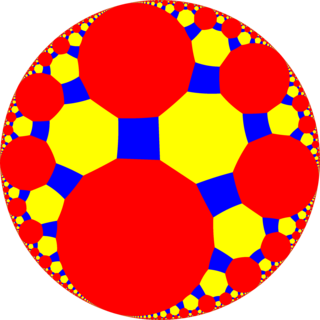
In geometry, the truncated tetraapeirogonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one octagon, and one apeirogon on each vertex. It has Schläfli symbol of tr{∞,4}.

In geometry, the truncated tetrahexagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one decagon, and one dodecagon on each vertex. It has Schläfli symbol of t_0,1,2{6,5}. Its name is somewhat misleading: literal geometric truncation of pentahexagonal tiling produces rectangles instead of squares.

In geometry, the truncated hexaoctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one dodecagon, and one hexakaidecagon on each vertex. It has Schläfli symbol of tr{8,6}.

In geometry, the truncated order-6 octagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{8,6}.

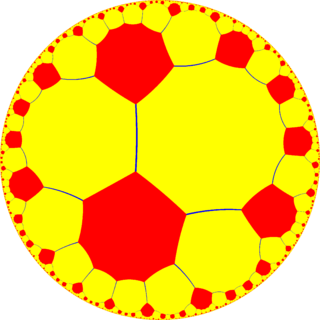
In geometry, the truncated order-8 hexagonal tiling is a semiregular tiling of the hyperbolic plane. It has Schläfli symbol of t{6,8}.

References

John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
"Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

John Horton Conway FRS is an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He has also contributed to many branches of recreational mathematics, notably the invention of the cellular automaton called the Game of Life. Conway spent the first half of his long career at the University of Cambridge, in England, and the second half at Princeton University in New Jersey, where he now holds the title Professor Emeritus.

International Standard Book Number Unique numeric book identifier

The International Standard Book Number (ISBN) is a numeric commercial book identifier which is intended to be unique. Publishers purchase ISBNs from an affiliate of the International ISBN Agency.

External links

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.